复习视频

XiaoXianYue原创2024年12月27日大约 7 分钟

ch 07 支持向量机

零散知识点

SVM 本质上是线性的，但是可以通过核函数把非线性数据弄成线性的、高维的数据。
Kernel function (干嘛的？) —— 把数据在高维弄成线性的，输入两个低维向量，输出内积（即他们的关系）
- As long as the kernel matrix corresponding to a symmetric function is semi-positive definite, it can be used as a kernel function.

Dual Problem

数据要有强凸的特性，原问题才能与对偶问题对等

用核函数把数据映射到了一个很高的维度，怎么计算？只需要知道内积 $x_{i}^{T} x$ 就可以了

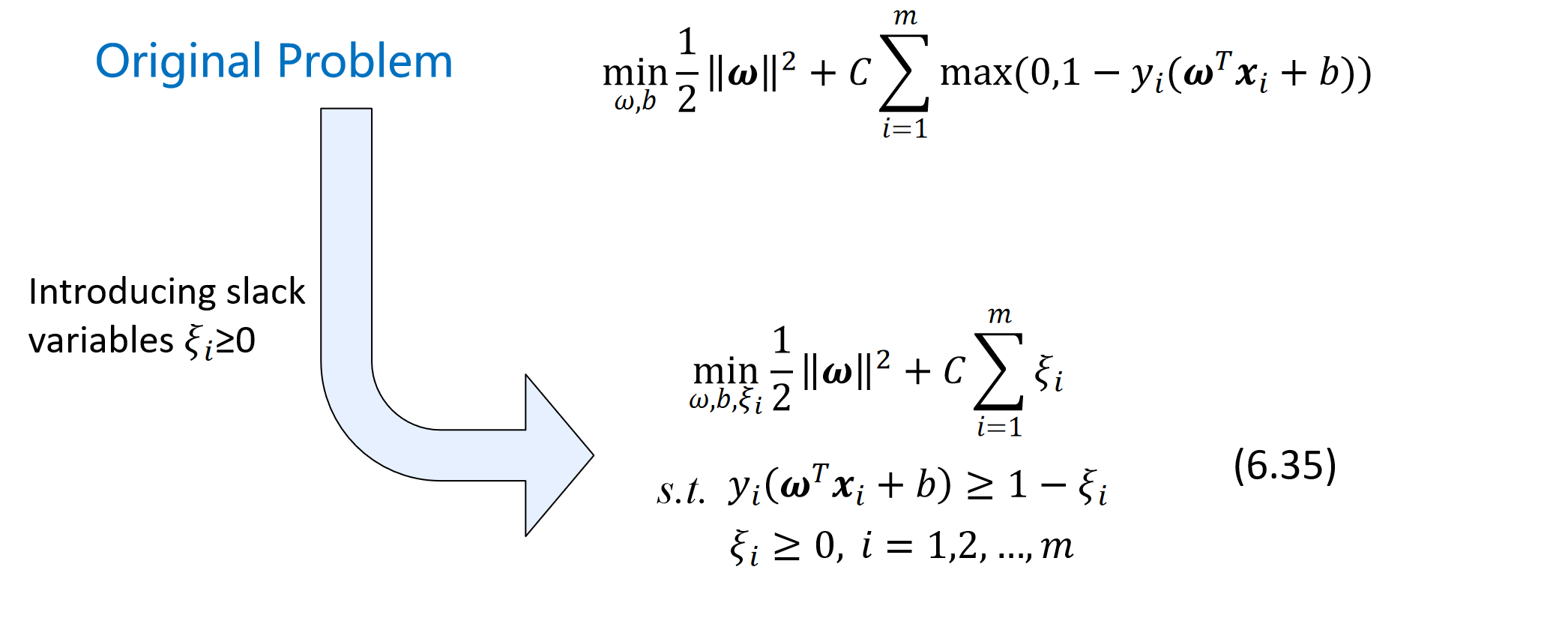
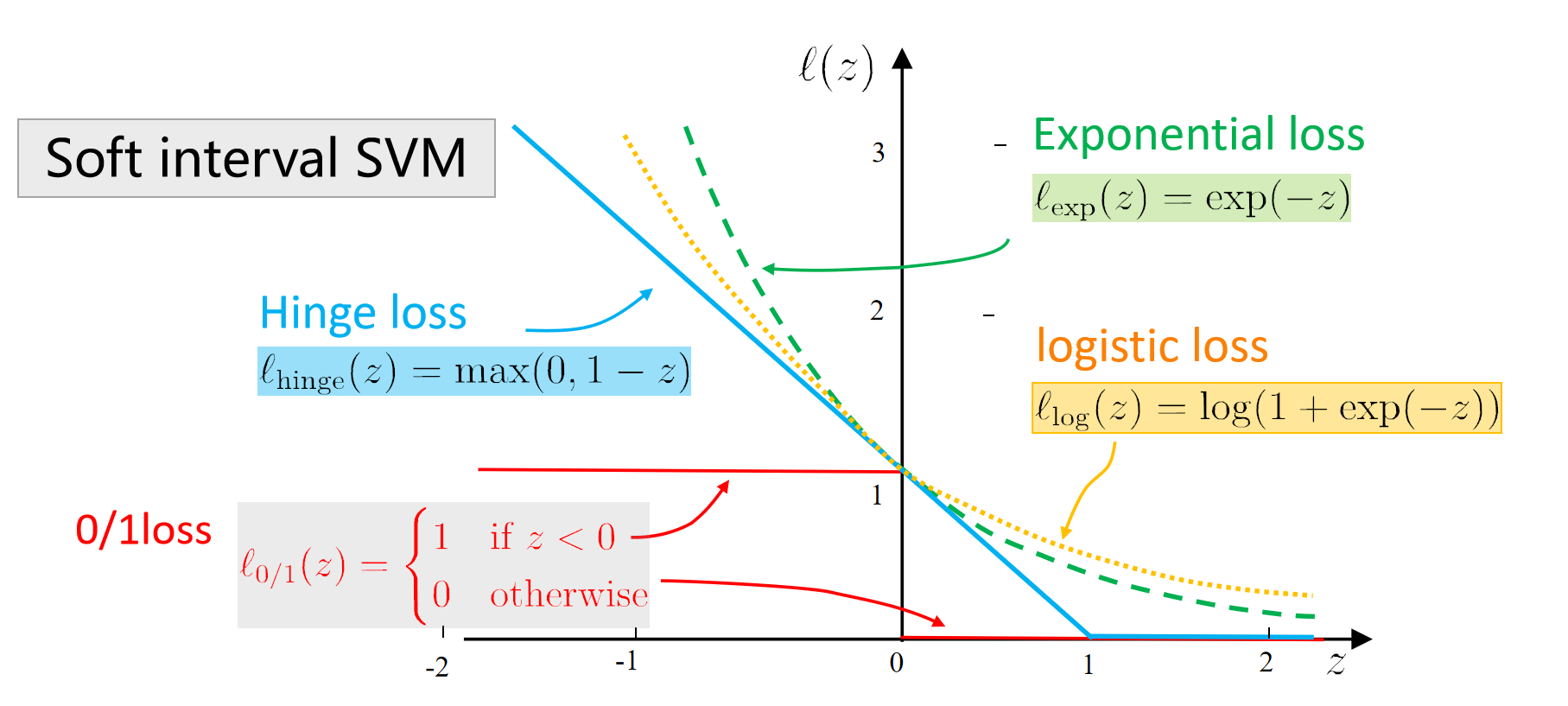
ch 08 决策树

决策树是非线性的

构建决策树

子树 1：`Outlook = Sunny`

对于 Outlook = Sunny 的子数据集，样本如下：

Sunny, Hot, High, False, No
Sunny, Hot, High, True, No
Sunny, Mild, High, False, No
Sunny, Cool, Normal, False, Yes
Sunny, Mild, Normal, True, Yes

样本统计：
- Yes = 2
- No = 3

1. 计算 `Sunny` 数据集的熵：

$E n t (D_{S u n n y}) = - \frac{2}{5} \log_{2} (\frac{2}{5}) - \frac{3}{5} \log_{2} (\frac{3}{5}) \approx 0.971$

2. 计算剩余属性的信息增益：

对剩余的三个属性（Temperature, Humidity, Windy）分别计算信息增益：

属性 Temperature：
- Hot: [No, No]
- Mild: [No, Yes]
- Cool: [Yes]
- 熵计算后，条件熵为 $E n t (D | Temperature) \approx 0.57$ ，对应的信息增益为 $0.971 - 0.57 = 0.401$ 。
属性 Humidity：
- High: [No, No, No]
- Normal: [Yes, Yes]
- 熵计算后，条件熵为 $E n t (D | Humidity) \approx 0.0$ ，对应的信息增益为 $0.971 - 0.0 = 0.971$ 。
属性 Windy：
- False: [No, No, Yes]
- True: [No, Yes]
- 熵计算后，条件熵为 $E n t (D | Windy) \approx 0.6$ ，对应的信息增益为 $0.971 - 0.6 = 0.371$ 。

3. 选择最佳属性：

Humidity 的信息增益最大（0.971），因此选择 Humidity 作为划分属性。

4. 生成子节点：

Outlook = Sunny
├── Humidity = High -> No
└── Humidity = Normal -> Yes

子树 2：`Outlook = Overcast`

对于 Outlook = Overcast 的子数据集，样本如下：

Overcast, Hot, High, False, Yes
Overcast, Cool, Normal, True, Yes
Overcast, Mild, High, True, Yes
Overcast, Hot, Normal, False, Yes

样本统计：
- Yes = 4
- No = 0

熵计算：

因为所有样本属于同一类别：

$E n t (D_{O v e r c a s t}) = 0$

结论：

该子节点已经纯净，无需进一步划分。最终子节点为：

Outlook = Overcast -> Yes

子树 3：`Outlook = Rainy`

对于 Outlook = Rainy 的子数据集，样本如下：

Rainy, Mild, High, False, Yes
Rainy, Cool, Normal, False, Yes
Rainy, Cool, Normal, True, No
Rainy, Mild, Normal, False, Yes
Rainy, Mild, Normal, True, No

样本统计：
- Yes = 3
- No = 2

1. 计算 `Rainy` 数据集的熵：

$E n t (D_{R a i n y}) = - \frac{3}{5} \log_{2} (\frac{3}{5}) - \frac{2}{5} \log_{2} (\frac{2}{5}) \approx 0.971$

2. 计算剩余属性的信息增益：

对剩余的三个属性（Temperature, Humidity, Windy）分别计算信息增益：

属性 Temperature：
- Mild: [Yes, Yes, No]
- Cool: [Yes, No]
- 熵计算后，条件熵为 $E n t (D | Temperature) \approx 0.95$ ，对应的信息增益为 $0.971 - 0.95 = 0.021$ 。
属性 Humidity：
- High: [Yes]
- Normal: [Yes, Yes, No, No]
- 熵计算后，条件熵为 $E n t (D | Humidity) \approx 0.8$ ，对应的信息增益为 $0.971 - 0.8 = 0.171$ 。
属性 Windy：
- False: [Yes, Yes, Yes]
- True: [No, No]
- 熵计算后，条件熵为 $E n t (D | Windy) \approx 0.0$ ，对应的信息增益为 $0.971 - 0.0 = 0.971$ 。

3. 选择最佳属性：

Windy 的信息增益最大（0.971），因此选择 Windy 作为划分属性。

4. 生成子节点：

Outlook = Rainy
├── Windy = False -> Yes
└── Windy = True -> No

总结

最终生成的决策树如下：

Outlook
├── Sunny
│   ├── Humidity = High -> No
│   └── Humidity = Normal -> Yes
├── Overcast -> Yes
└── Rainy
    ├── Windy = False -> Yes
    └── Windy = True -> No

这个过程使用了信息增益计算每一步的划分依据，并递归处理子节点，直到所有节点纯净或无法划分为止。

ch 09

先验概率 $P (c_{j})$ 是在没有观察到具体数据 x 时，类别 $c_{j}$ 发生的概率。它反映了我们对类别分布的先验知识，通常基于经验、历史数据或均匀假设。
最大似然函数 $P (x | c_{j})$ 表示在类别 $c_{j}$ 下，观察到数据 x 的概率。最大似然估计是寻找模型参数，使得训练数据的联合概率 $P (x | c_{j})$ 最大。
最小分类误差，就要最大后验概率 $P (c | x)$ 即数据 x 被分为 c 的概率是最大的。

$P (c | x) = \frac{P (x | c) P (c)}{P (x)}$

贝叶斯是一种经典的 Generative model
生成式模型：朴素贝叶斯；混合高斯
Discriminate model ：逻辑回归、SVM、神经网络、KNN

一个朴素贝叶斯算法的操作

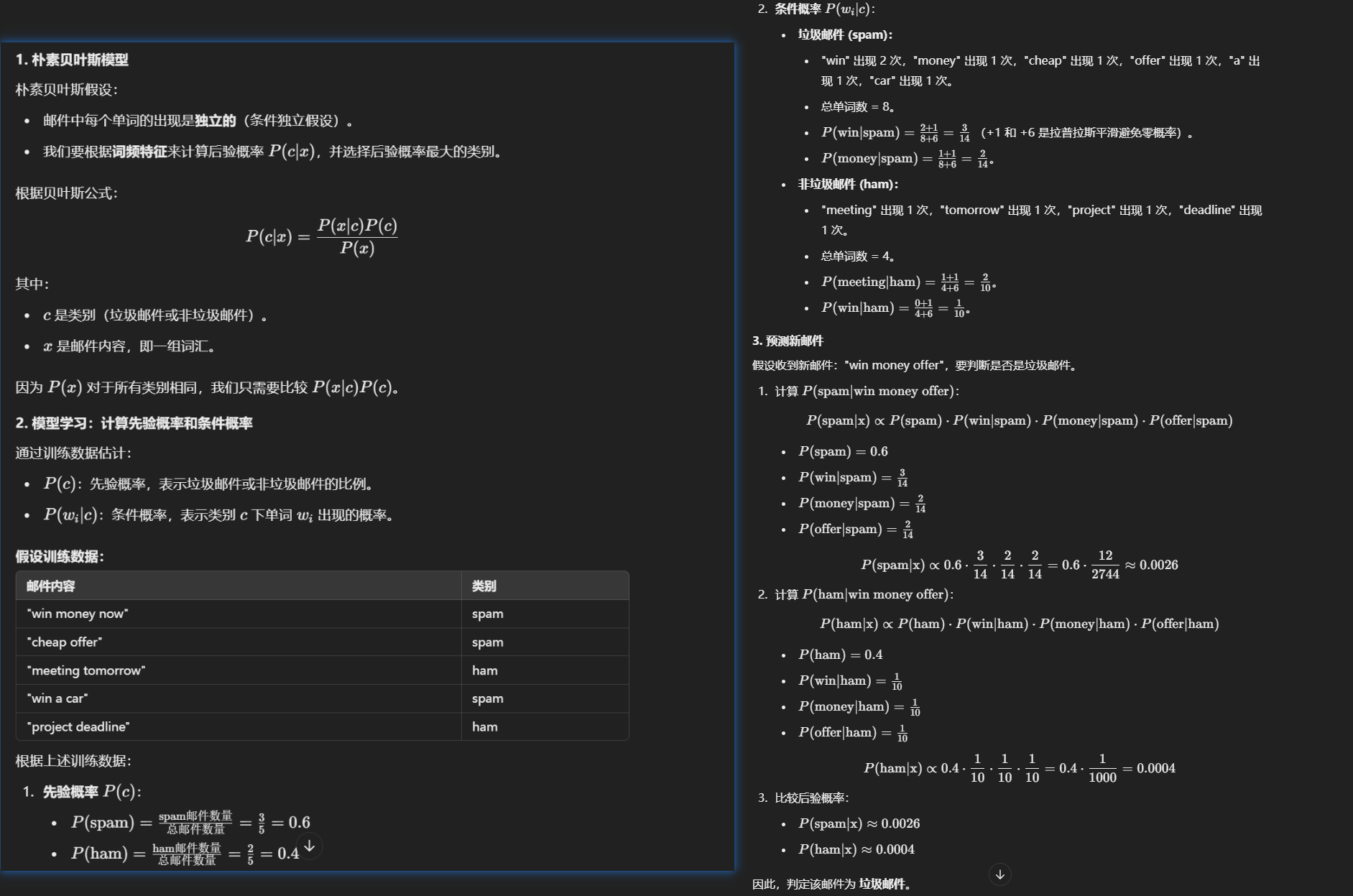
拉普拉斯平滑

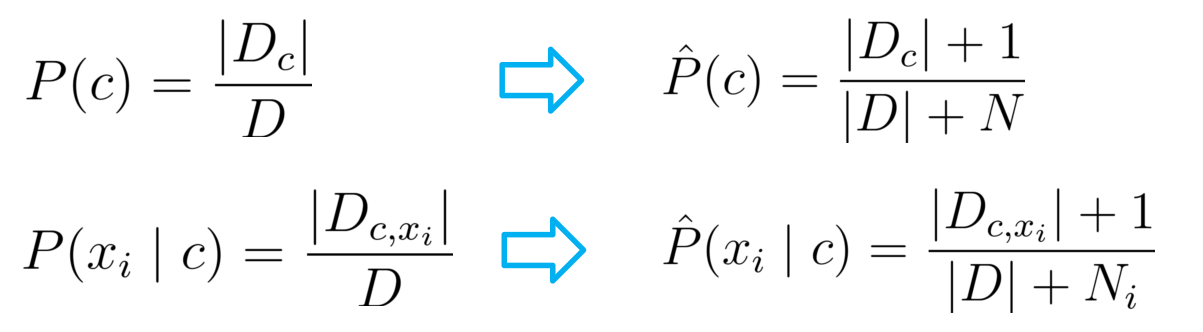
两个大 N ？

Semi-Naive

SPODE: 超父节点，所有点都与一个有关。（如温度，湿度，空气等都与天气有关）。

都是从给的数据集中算出的。

TAN：树状的，算出两两的互信息，作最大生成树的权重。

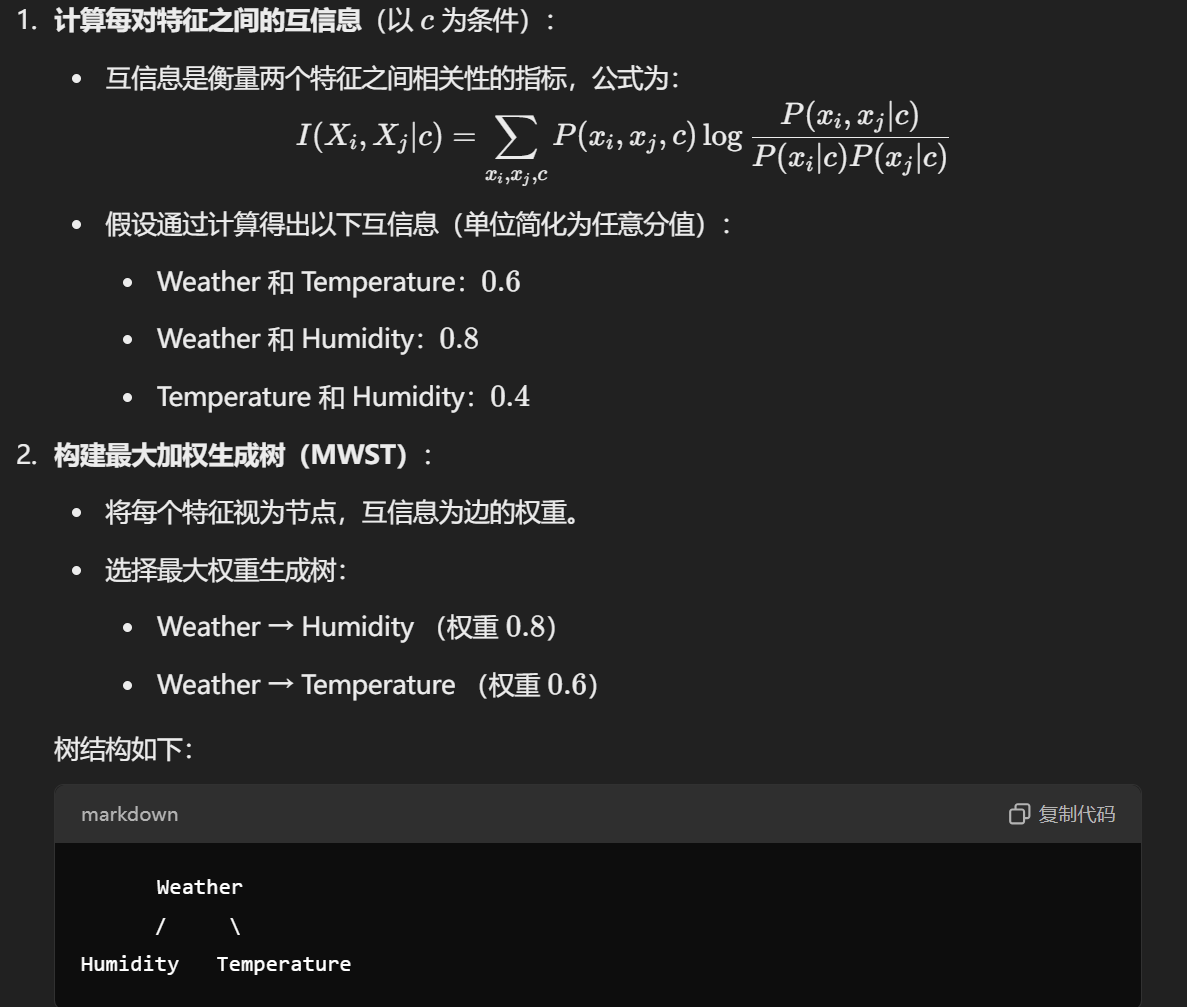
AODE：
- 多模型平均：AODE 会考虑多个特征作为父节点，每个特征生成一个 SODE，然后将所有模型的预测结果平均。
- 稳健性：通过平均多个模型，AODE 减少了因选择单一特征而可能导致的误差。

ch 10 集成学习

要求结果的准确性和多样性。

Boosting

AdaBoost

AdaBoost is only suitable for binary classification tasks
比较注重于减少偏差

Bagging

Bagging 就是行取样，Random Forest 就是列取样。
OOB 用剩下三分之一取不到的作模型评估。

ch 11 聚类算法

内外部指标
值度量差异（VDM）：
- 公式核心：通过离散值在不同类别上的分布差异，衡量它们的“距离”。
- 适用场景：适用于离散属性的分类或聚类任务，尤其是需要捕捉值间差异的场景。
- 优势：比简单的“是否相同”更细致地处理离散值间的相似性。

Prototype Clustering

通常情况下，算法首先初始化原型，然后迭代更新原型以求解。

Density

噪音鲁棒。

ch 12

LLE

为什么 LLE 是非线性降维？

局部线性假设：
- 在高维空间中，LLE 假设每个数据点的邻域可以用其邻居点的线性组合来表示（局部线性假设）。
- 然而，这种线性关系只在数据的局部范围内成立，整体上数据可能分布在复杂的非线性流形上。
全局非线性映射：
- 在降维过程中，LLE 保留的是数据点在局部邻域中的线性关系，并通过这些局部关系重建全局的非线性结构。
- 因此，LLE 能够揭示数据的非线性结构，适合处理复杂流形数据。

特性	LLE	PCA
假设	数据局部线性，整体非线性	数据整体线性
结构保留	局部几何结构	全局方差结构
映射方式	非线性降维	线性降维
计算方法	局部重构权重 + 全局优化	协方差矩阵特征值分解
适用场景	非线性流形数据	线性分布数据

方法	距离处理方式
LLE	利用高维空间中的欧氏距离计算点的邻域，但之后主要保留点与邻居点之间的局部线性关系，不直接涉及全局距离。
Isomap	构造图上的最短路径，近似流形上的“测地距离”，测地距离能够更准确地反映非线性流形上的全局几何结构，从而保留全局距离关系。

Metric Learning

人脸识别：

如果两个照片是同一个人，它们的距离应该很近；
如果是不同的人，距离应该很远。
Metric Learning 会训练一个模型，让这种“近”与“远”符合实际要求。

图片搜索：

假如你上传了一张猫的照片，希望搜索到相似的猫图片。
Metric Learning 会学习一种“图片距离”，让相似的猫图片离查询图片很近，而其他动物的图片离得远。

推荐系统：

通过学习用户与物品之间的相似性，Metric Learning 会让用户喜欢的商品离得更近，而不感兴趣的商品离得更远。