机器学习第5章
Linear Regression
What’s the linear regression
监督学习 (Supervised learning):
学习样本定义为预测结果
这对应于 线性回归 (Linear Regression),即模型尝试找到输入 x 和输出 y 之间的线性关系来进行预测。预测结果
这对应于 对数几率回归 (Log-odds Regression),通常用于分类问题,例如二分类任务。线性回归像是一把直尺,可以测量任意大小(实数)的东西。
逻辑回归给这把直尺加了一个「限制」,比如测量的结果只能在 0 到 1 之间(通过 sigmoid 函数压缩),用来表示可能性。
详情

假设输入 x 和输出 y 之间存在线性关系 (Assume that there is a linear relationship between input x and output y):
这是线性模型的核心假设,即输出是输入的线性组合。
Type
Univariate Linear Regression
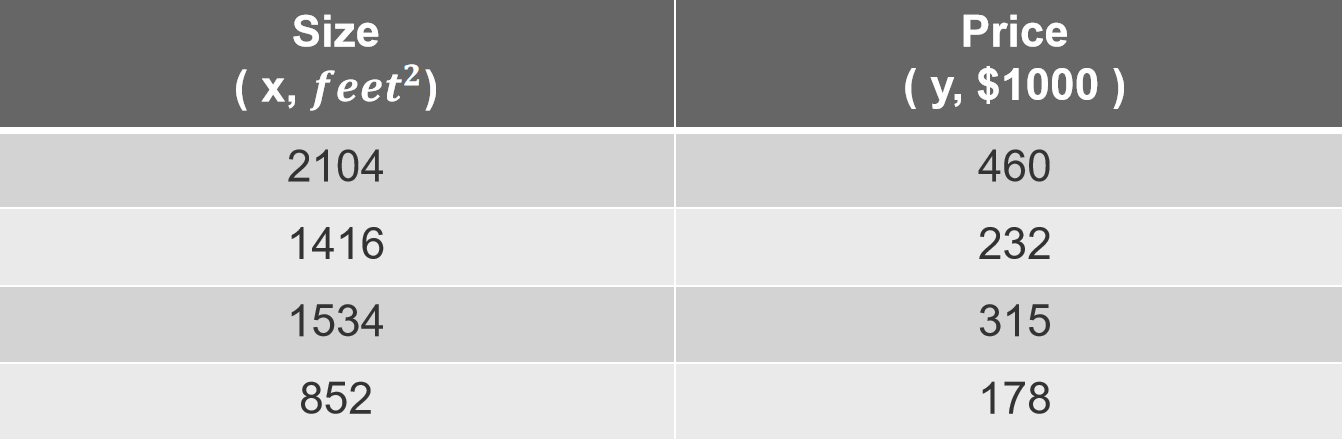
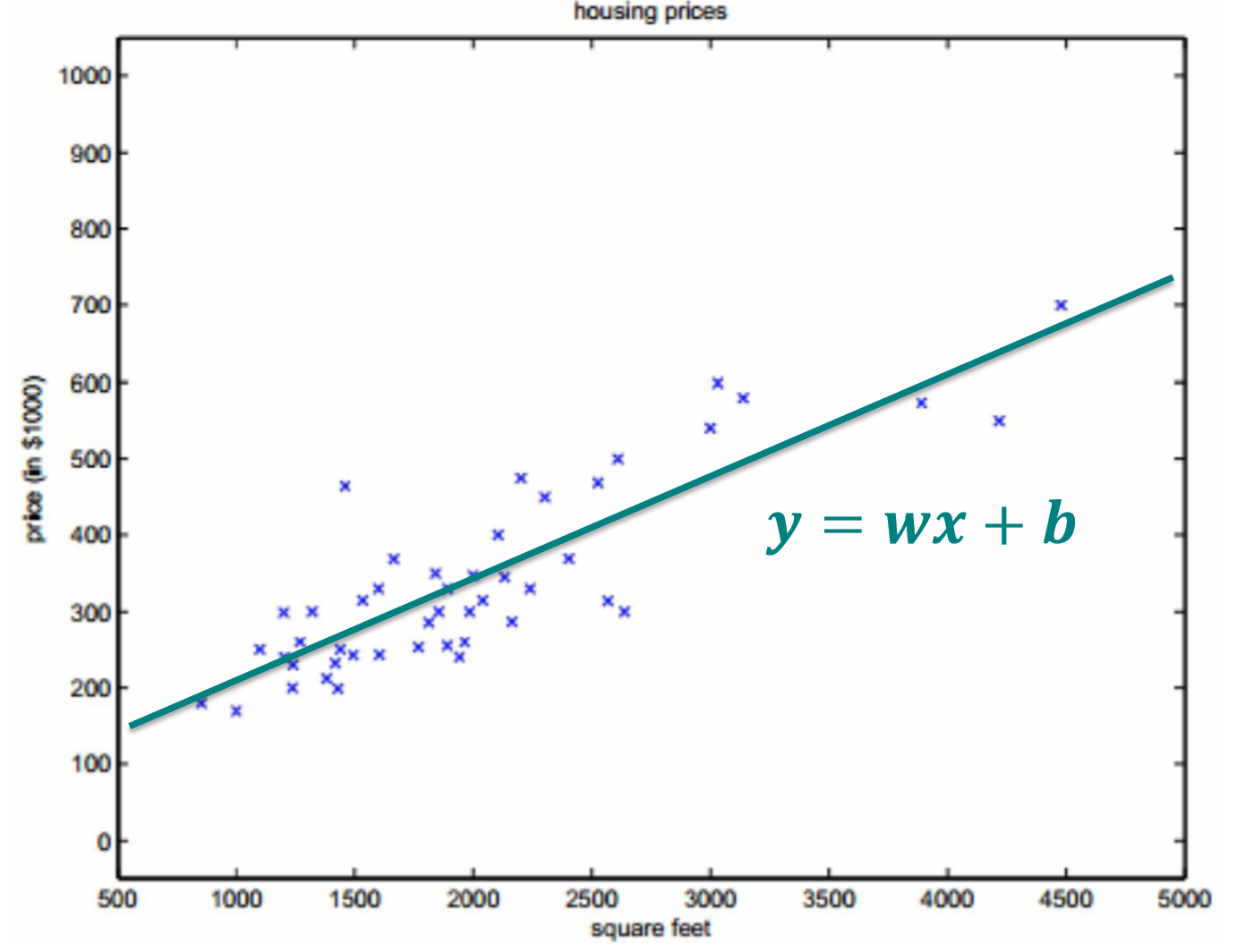
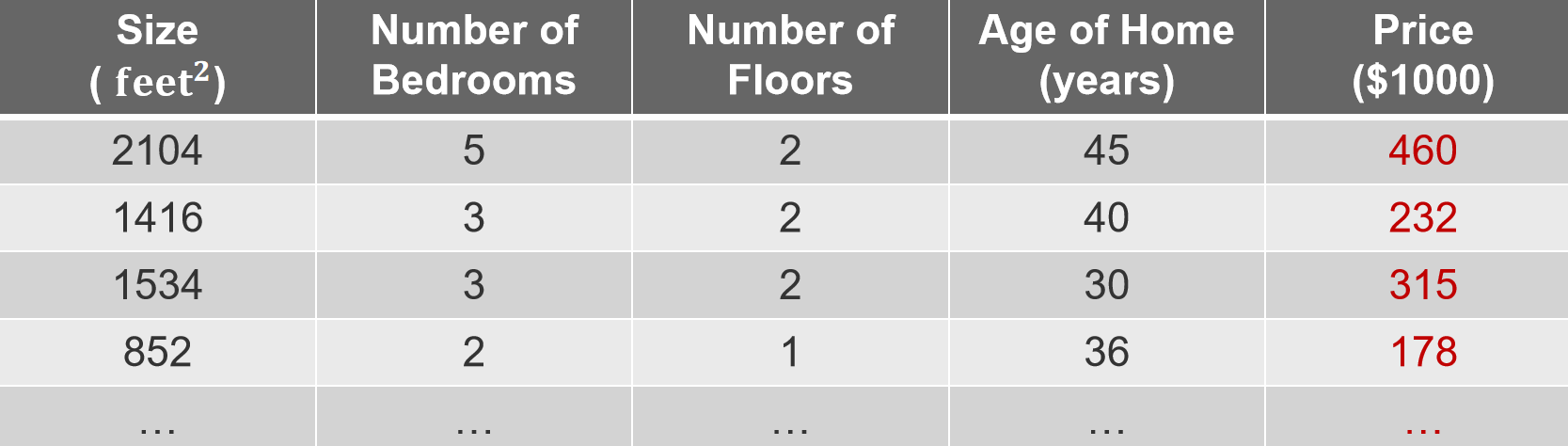
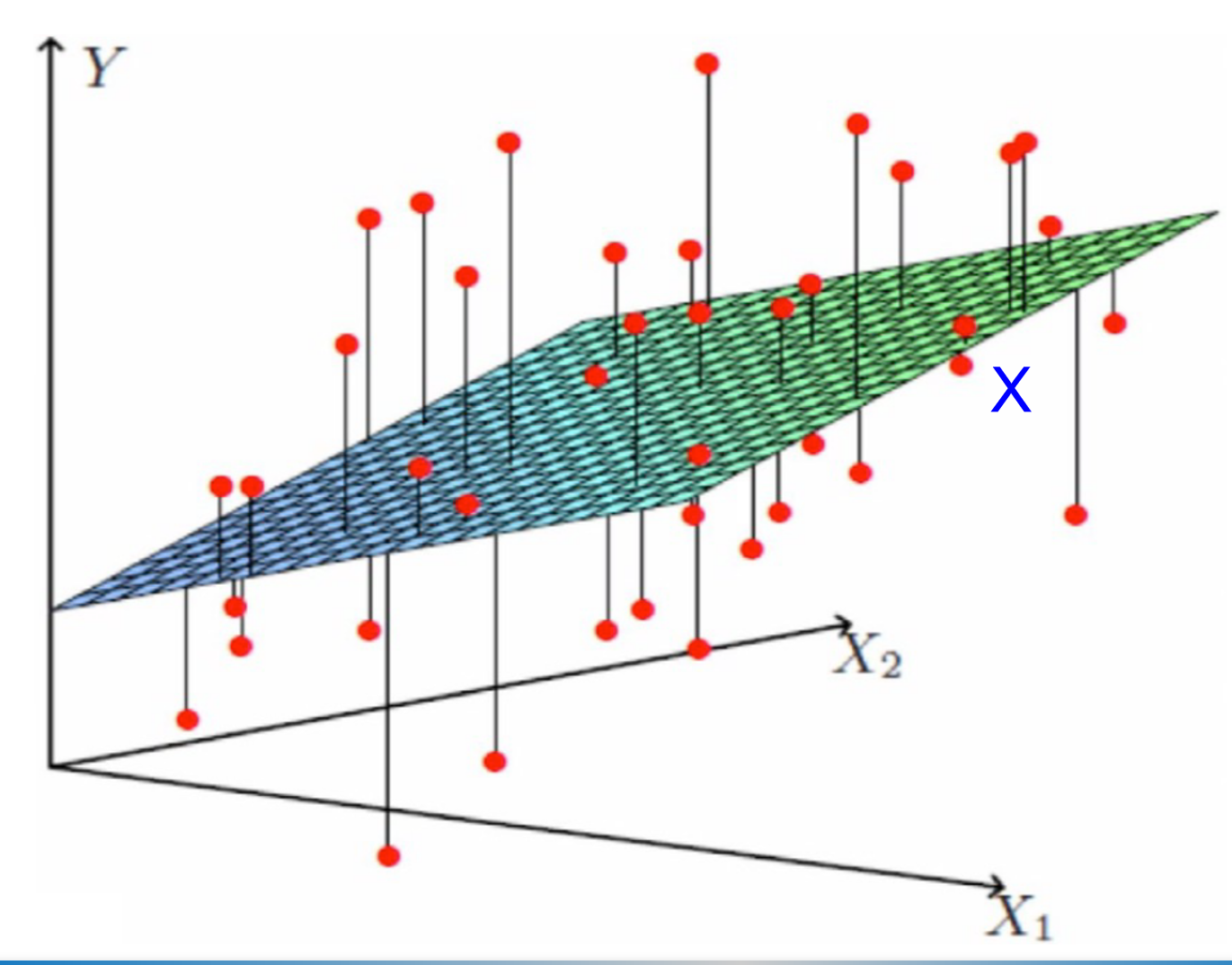
Multiple Linear Regression
Basic form
The general form of the linear model:
Vector form:
示例 (An Example):
判断西瓜品质的模型:
- 根蒂的系数最大 (0.5),表示根蒂对品质的影响最重要。
- 敲声的系数 (0.3) 大于色泽的系数 (0.2),说明敲声比色泽更重要。
Step
Step 1 Model
线性回归是函数的集合,例如:
准备好 Training set: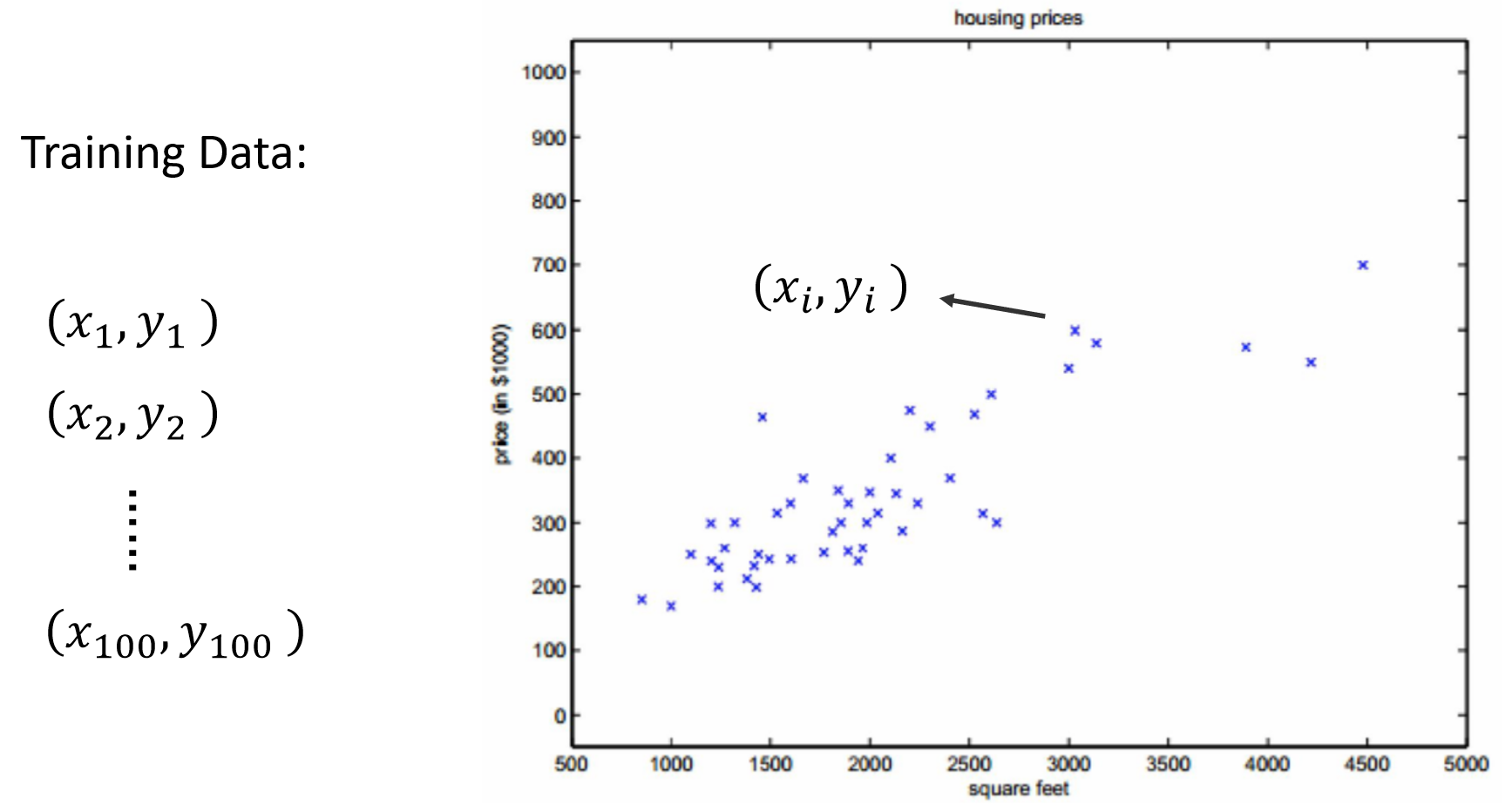
Step 2 Goodness of Function
问题背景:函数的优劣
- 给定一个模型
损失函数 L 的作用
- 定义: 损失函数 L 是一个用来衡量模型预测效果的指标,它的输入是一个函数
- 直观理解: 损失函数越小,说明模型的预测越接近真实值;反之,损失越大,模型效果越差。
均方误差

所以,可以用下面这个公式来进行 函数优劣性的评估
重要
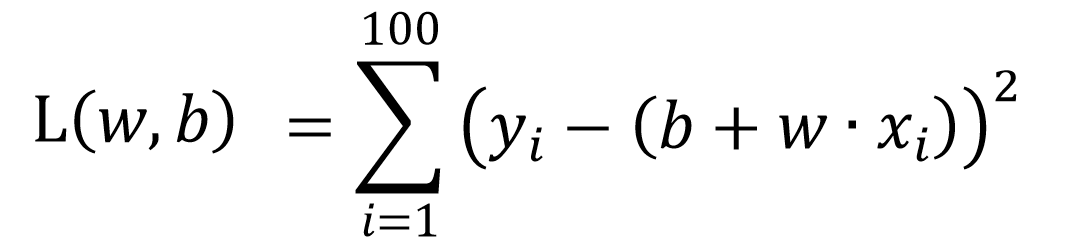
Step 3 Find Best Function
我们通过优化参数
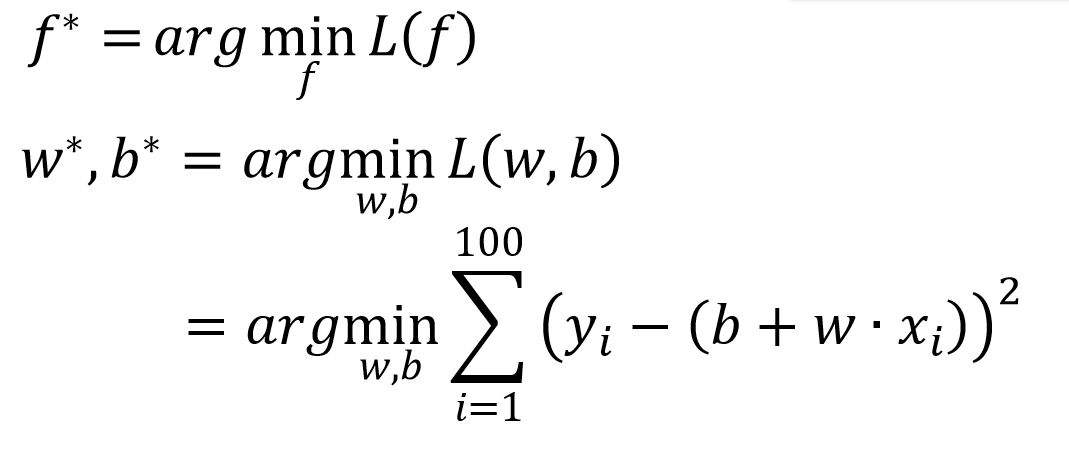
1. Least Squares Method
这个方法时候小数据模型。
用上面那个最优函数求偏导。


Gradient Descent
是 Step 3 中另外一种求最优解的方式。
重要
梯度是一个向量,表示函数值增加最快的方向,向量的大小表示变化率。
1. One parameter
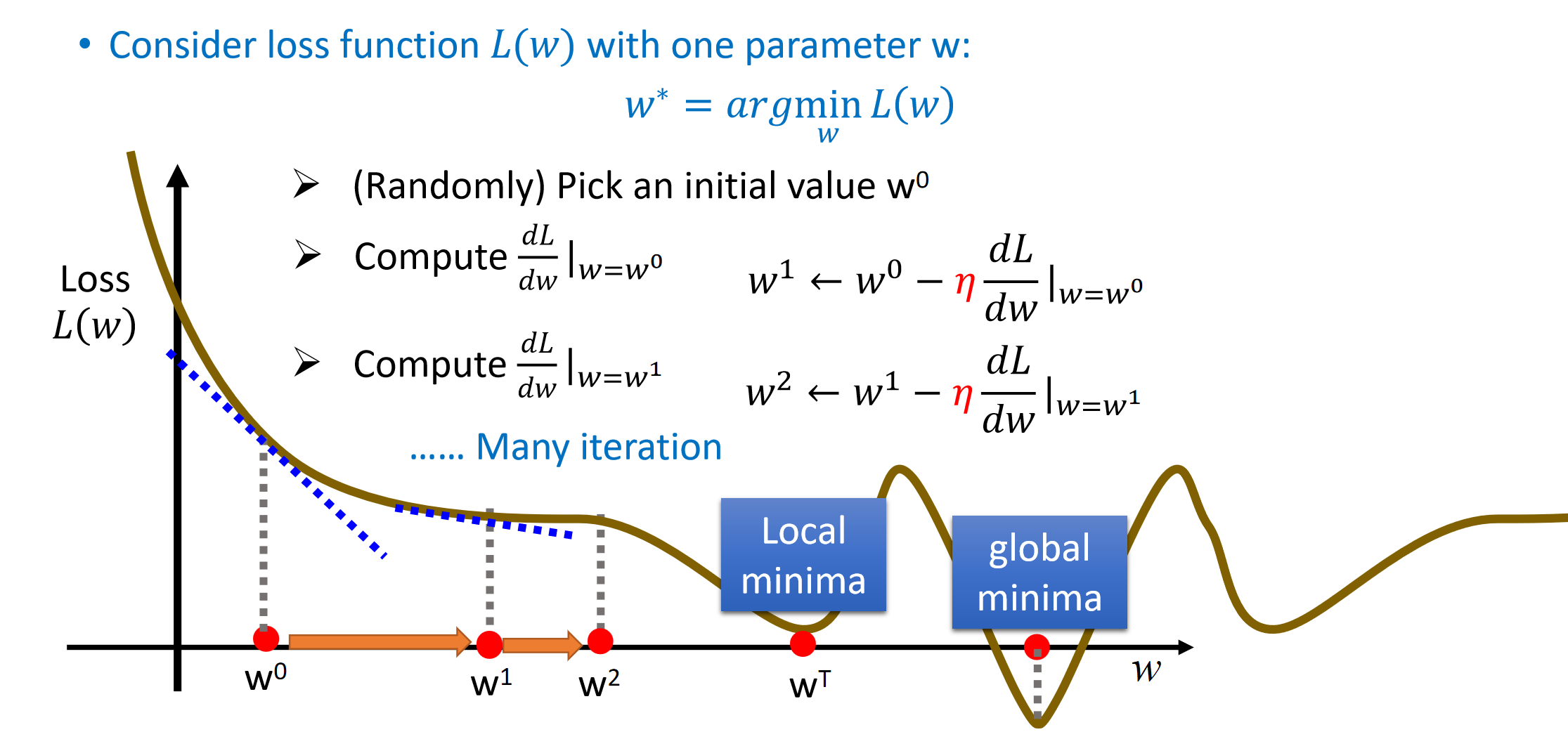
学习率
学习率
2. Two parameters

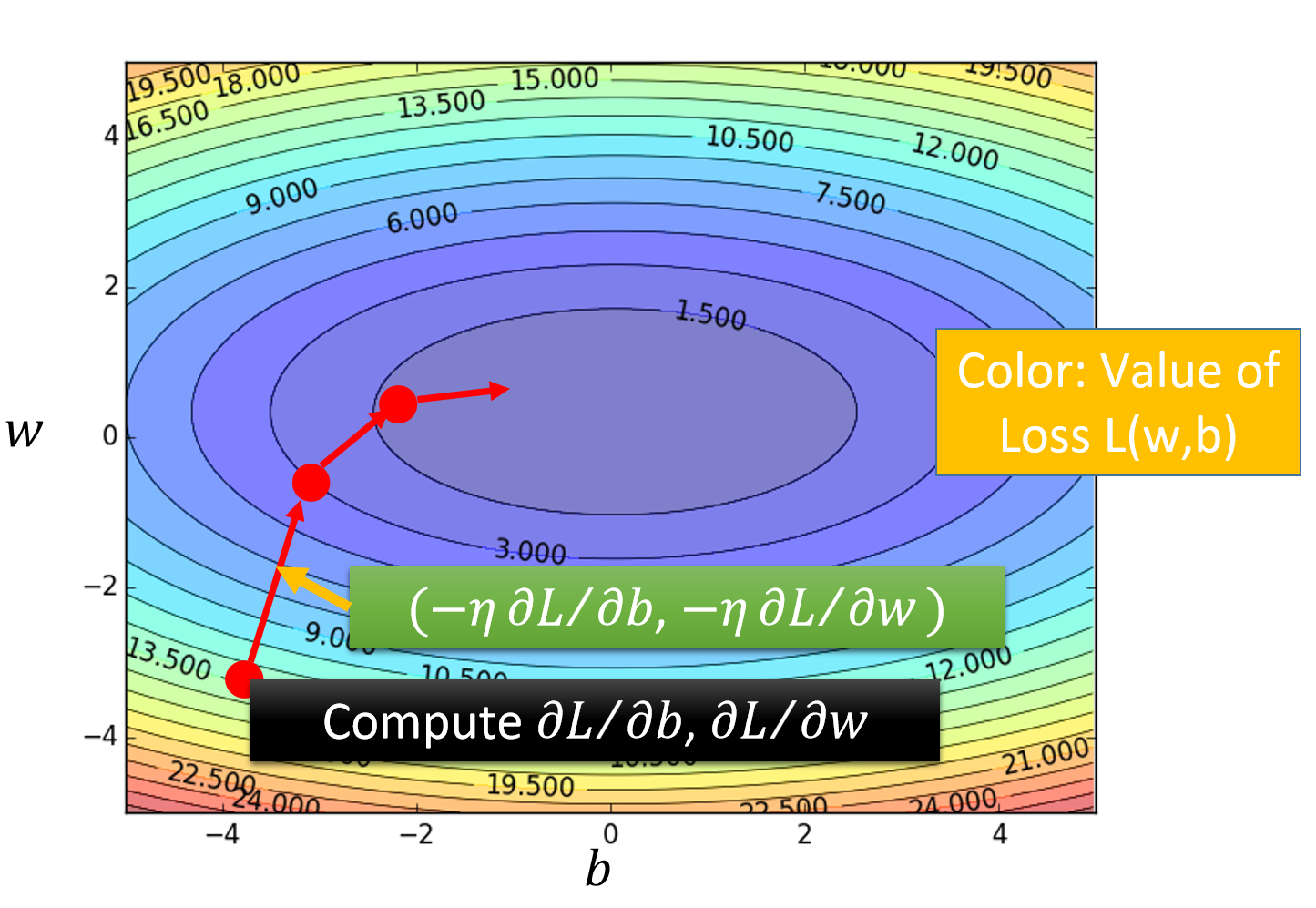
3. 实际操作中会出现的问题
Each time we update the parameters, we obtain θ that makes L(θ) smaller. 在每次操作过后,我们真的能保证我们的损失函数减少吗?
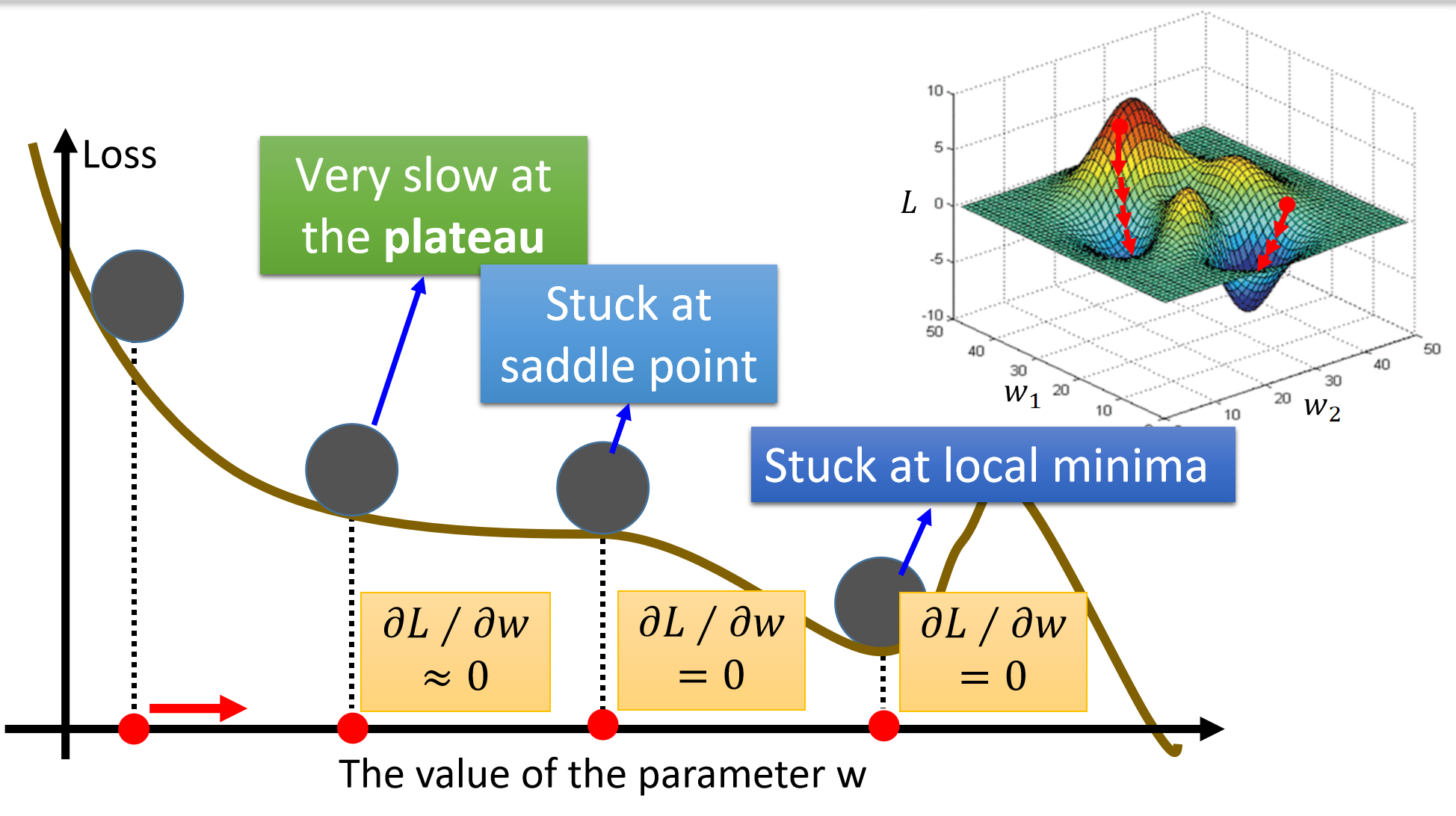
这张图里面显现了几种问题:
- Plateau(平坦区域):
- 当函数的梯度很小(接近零)时,更新幅度变得很小,收敛速度极慢。
- 在平坦区域(如高原),梯度下降会变得非常缓慢。
- Saddle Point(鞍点):
- 在多维空间中,某些点的梯度为零,但这些点既不是局部最小值也不是最大值。
- 梯度下降可能卡在鞍点附近,因为梯度为零时更新停止。
- Local Minima(局部最小值):
- 损失函数可能有多个局部最小值,梯度下降可能陷入局部最小值而非全局最优解。
- 优化算法可能需要逃离局部最小值。
Multiple Linear Regression
1. 数据集的定义
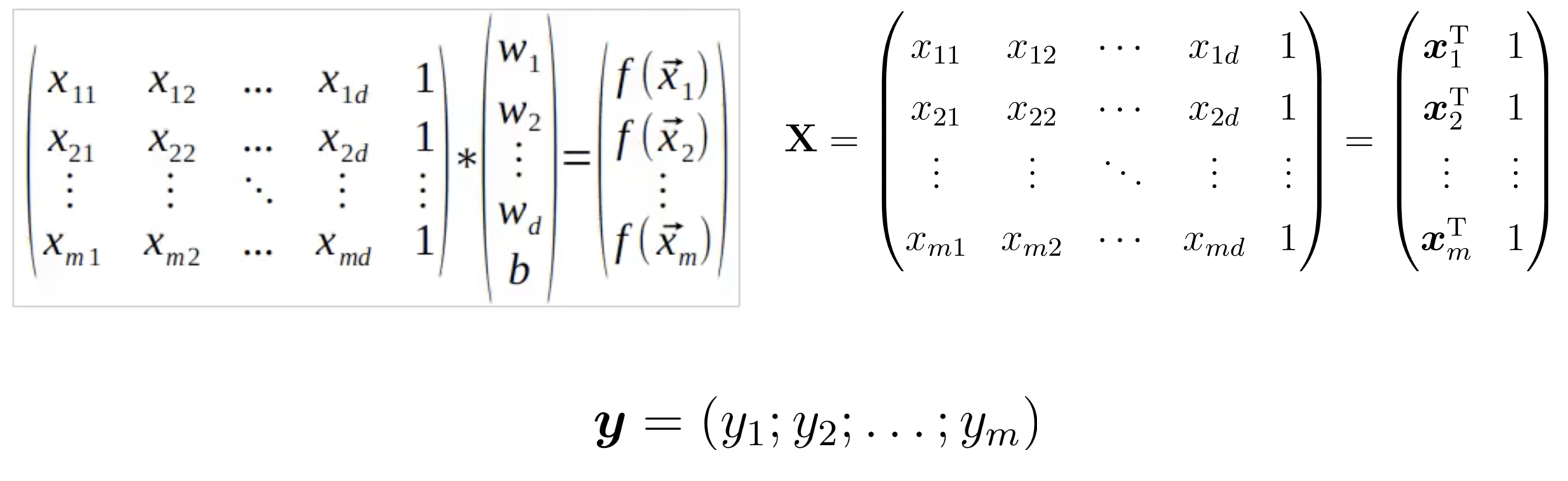
给定一个数据集
其中:
- 总共有
2. 多元线性回归目标
线性回归模型的目标是找到一组参数 w 和偏置 b,使得预测值
这里:
3. Least Squares Method
求解最优的
公式:
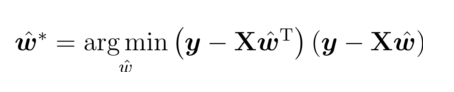
损失函数:
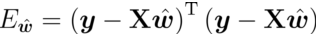
对于参数求偏导:
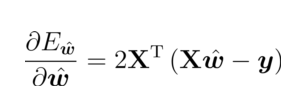
令导数为 0,求闭式解:
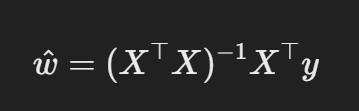
当
为满秩时,可以直接求解。 如果
不是满秩矩阵,则无法计算其逆矩阵。
Loglinear regression
The logarithm of the output label is the target approximated by the linear model.
输出标签的对数是线性模型近似的目标。
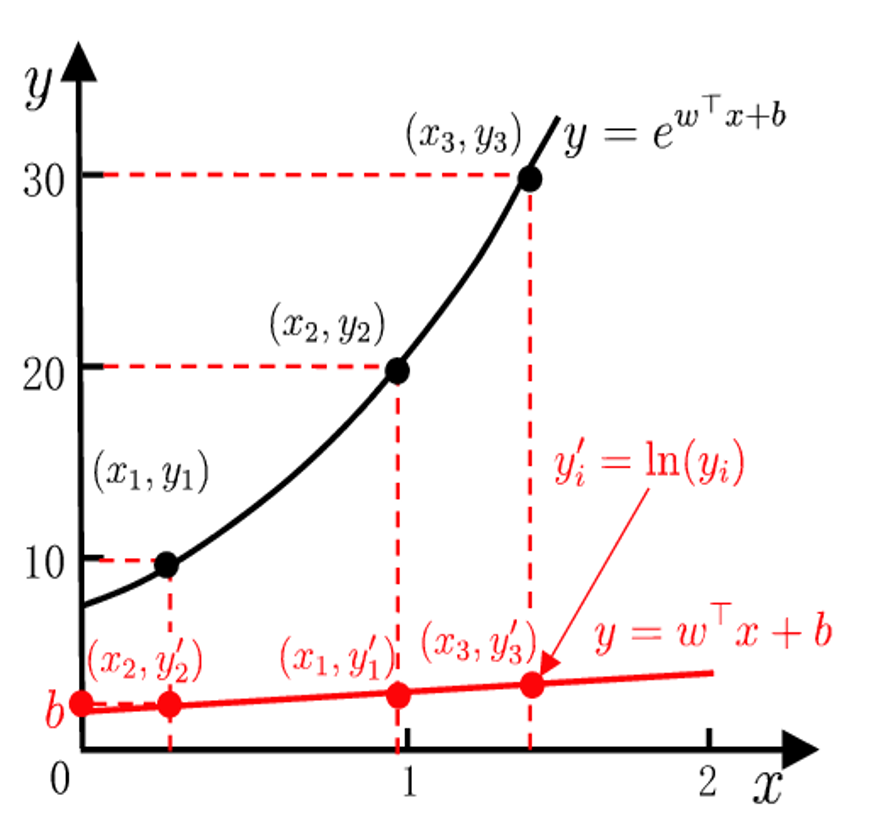
如果对目标变量 y 取自然对数
Binary Classification Task —— Logistic Regression
预测值和输出标签:
- 使用线性模型
找到一种函数,将分类标签与线性回归模型输出值联系起来。
理想函数
最理想的函数 - 单位阶跃函数:
如果预测值大于零,则判断为正样本;如果小于零,则判断为负样本。如果预测值等于零,可以任意判断。
但是单位阶跃函数是不连续的。这里我们可以引入逻辑函数。
替代优势
- 单调可微(Monotone differentiable)。
- 任意阶可微(Arbitrary order differentiable),使得梯度下降等优化方法适用。
公式:
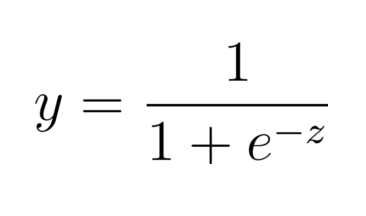
- 即 Sigmoid 函数,用于将线性结果映射到 (0,1)(0,1)(0,1) 的概率范围。
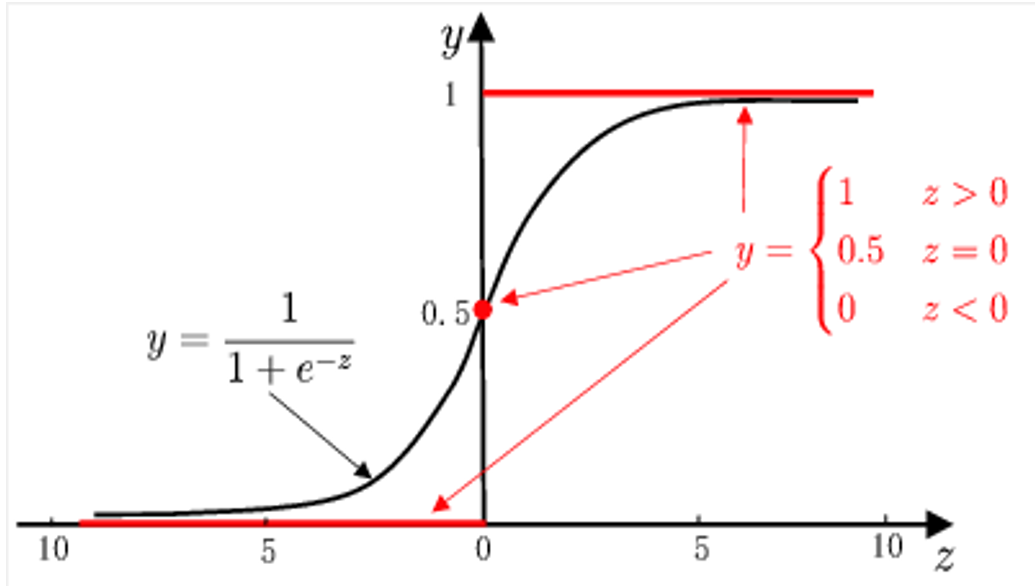
相关信息
仔细观察,逻辑函数的形式是否与逻辑回归很像?所以逻辑回归也可以用于分类问题!!
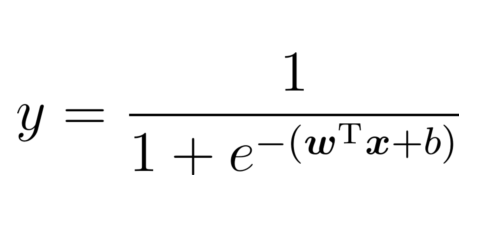
Log-odds 的意义
- 对数几率(Log-odds)公式:
逻辑回归的优势
- 无需先验分布假设:对输入数据分布无严格要求。
- 概率预测能力:直接输出属于某一类的概率值。
- 数值优化友好:可直接应用现有的优化算法(如梯度下降)来获得最优解。
Sigmoid 函数映射线性组合 z 到概率 y。
对数几率将概率 y 重新映射回线性组合 z。
Step 1 (Function Set)
逻辑回归模型,逻辑回归公式:
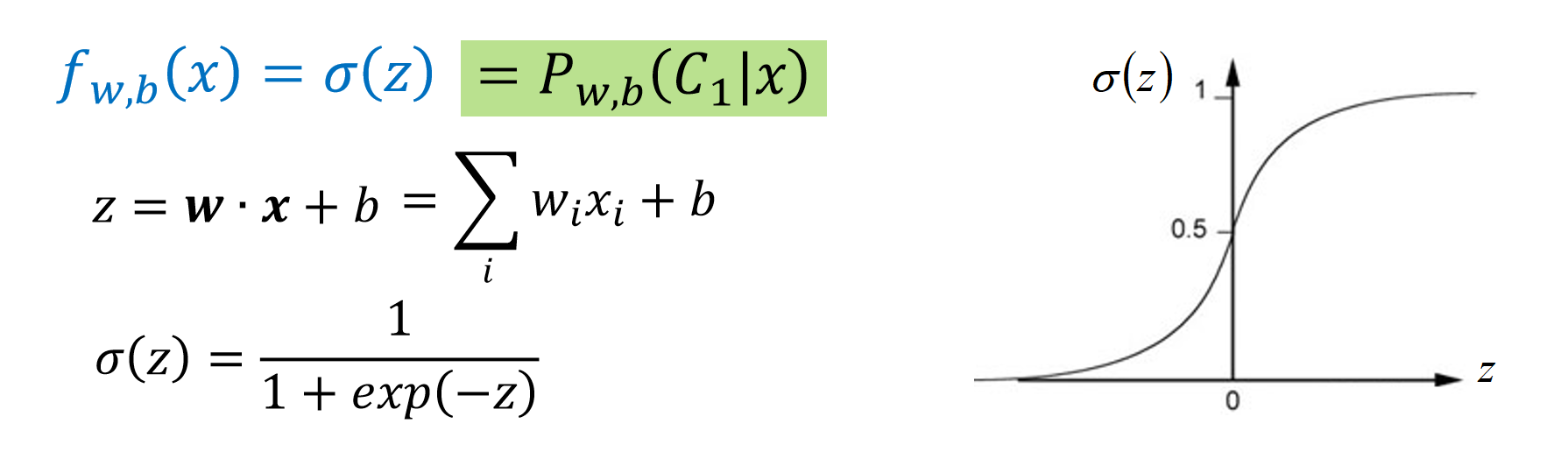
流程:
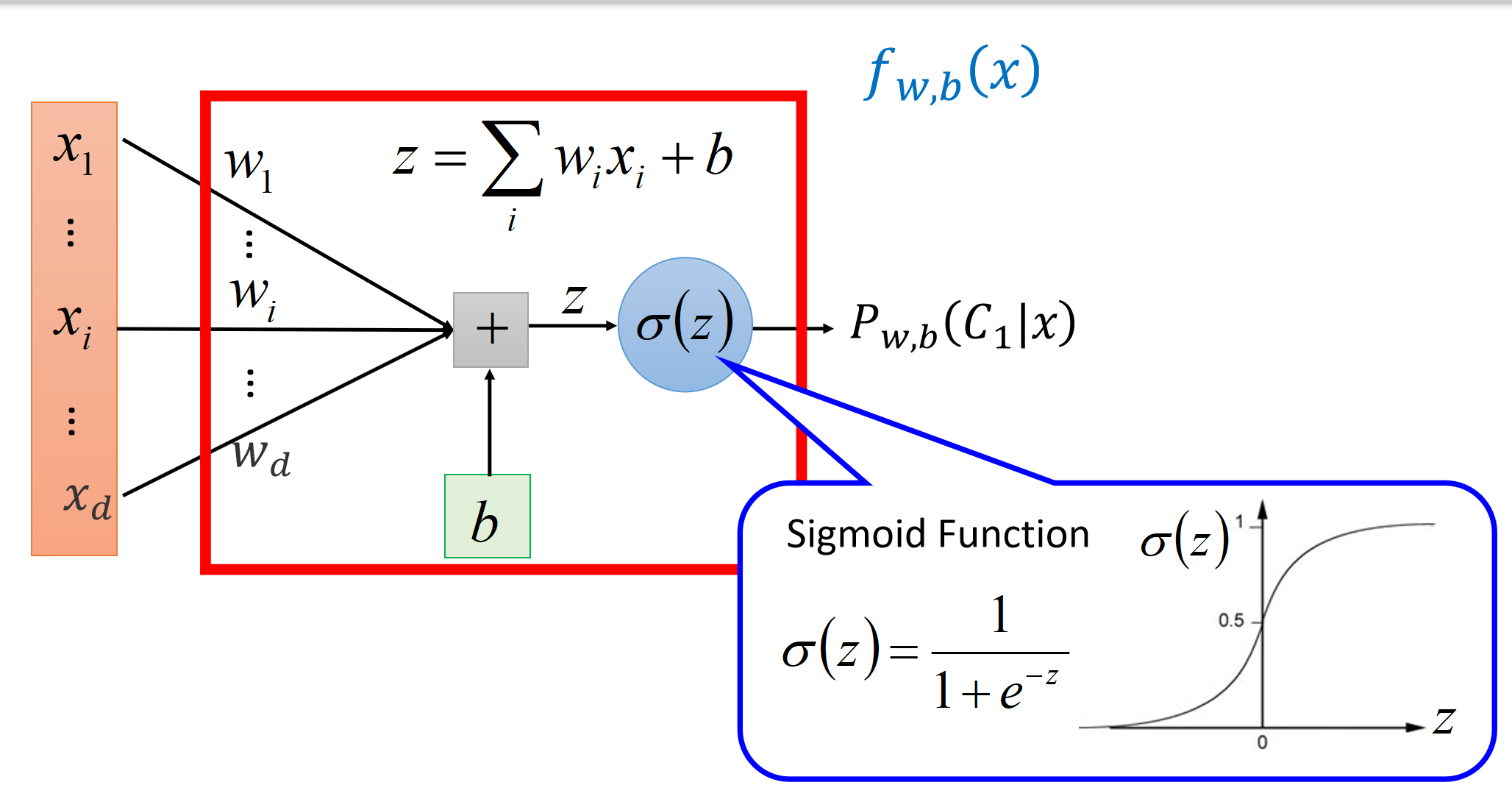
逻辑 & 线性模型选择

Step 2 (Goodness of a Function)
目标:找出函数的最大似然函数。
注
似然函数 L(w, b) 表示“在给定参数 w 和 b 的情况下,观测数据出现的概率”.
最大化似然等价于“解释数据最好”
- 定义似然函数:

- 我们需要找出一组 w,b 使得似然函数最大:
- 但是为了简化计算,我们可以取对数。对数似然函数是一个凸函数(对于逻辑回归),其最大值对应最优参数。
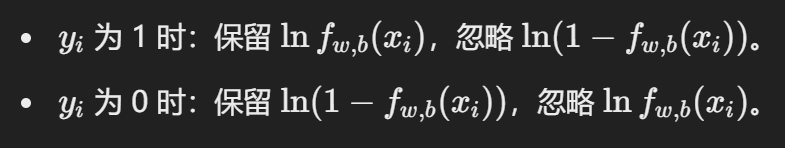
目标函数(负对数似然函数)与交叉熵(Cross-Entropy)之间的关系。
把对数似然函数取负,于是得到了负对数似然函数。
负对数似然实际上是交叉熵损失的特例,表示两个概率分布之间的差异。
交叉熵定义:
p(x) 是真实分布(标签),例如
q(x) 是模型预测分布
交叉熵
交叉熵越小,表示模型预测分布 q 越接近真实分布 p。
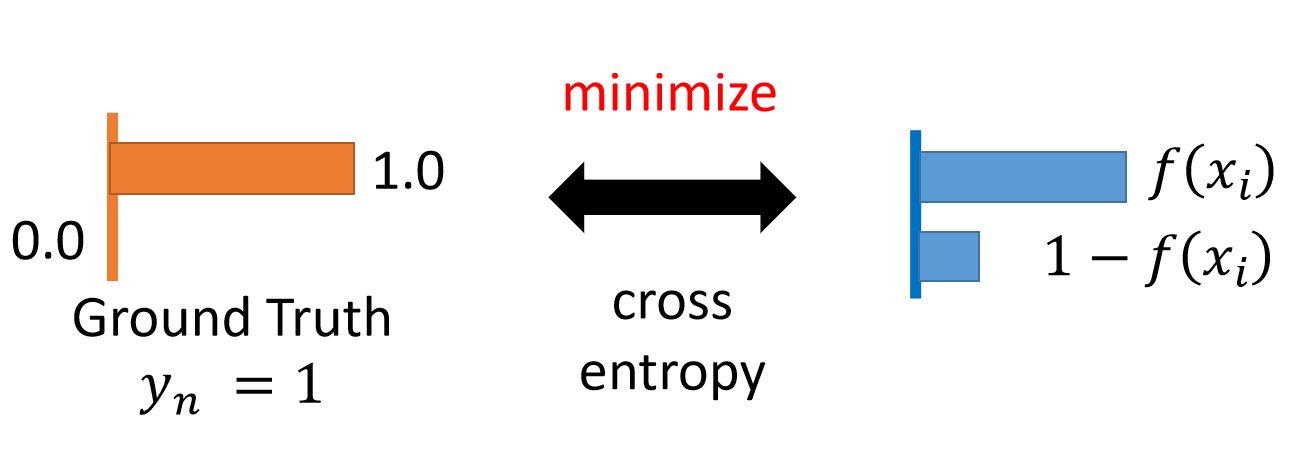
如图,左侧是真实分布,右侧是预测分布。交叉熵的工作原理:

Step 3(Find the Best function)
取偏导,前半部分:

后半部分:

最后发现交叉熵(逻辑回归)与平方误差(线性回归)的梯度下降公式是一样的:


为什么逻辑回归不能用平方误差当做损失函数??
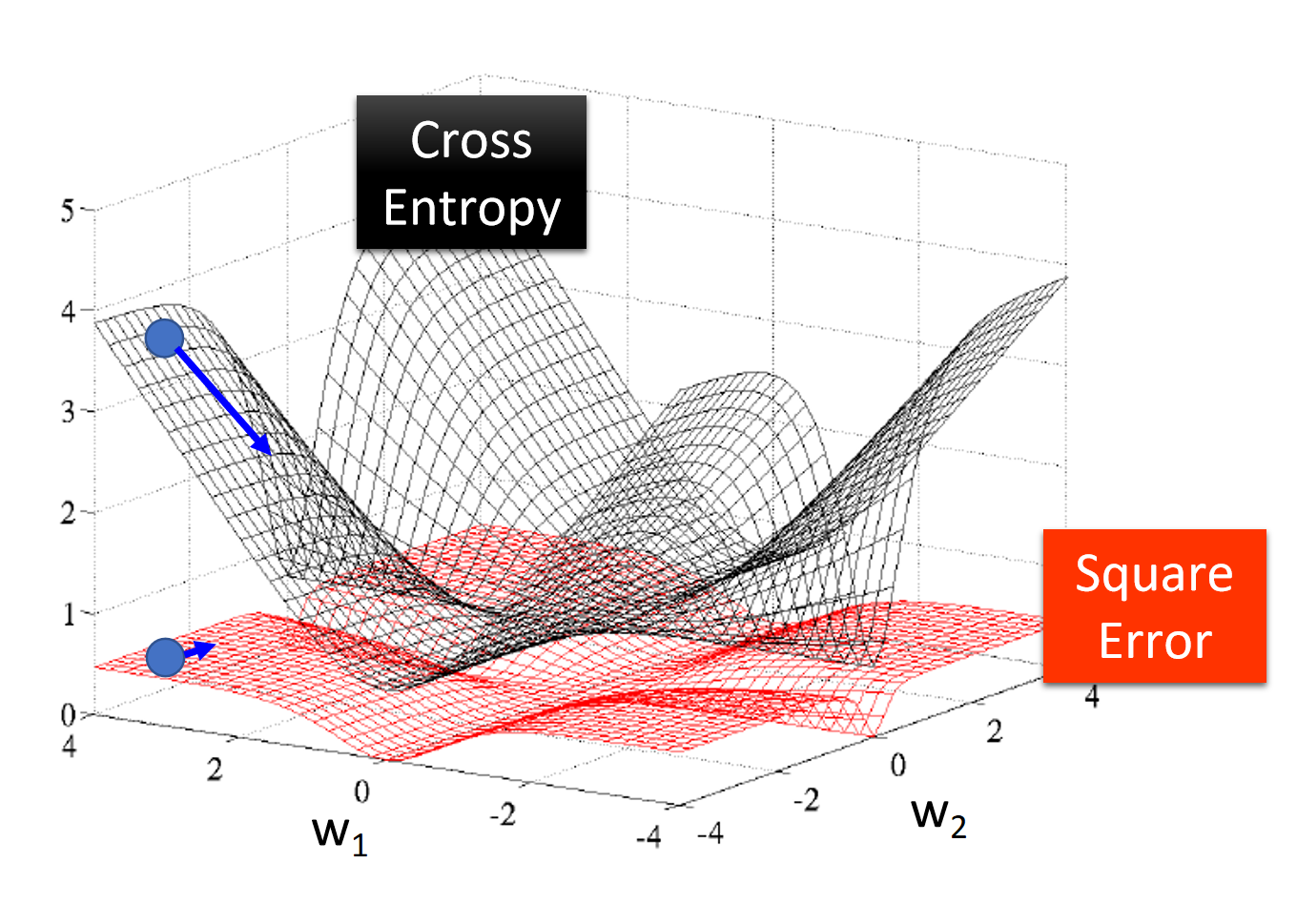
从图可以看出:
- 交叉熵损失(Cross Entropy)在参数空间中的损失面(黑色曲面)更陡峭、更清晰地引导梯度下降方向,容易找到最优解。
- 平方误差(Square Error)的损失面(红色曲面)较平滑,梯度较小,容易陷入局部最小值,尤其是在 Sigmoid 输出接近 0 或 1 时。


可以看出:当
问题:梯度为零意味着参数不再更新,但实际上此时模型还未达到最优解,仅仅是因为误差函数的特性导致更新停止。
这让我们看到了交叉熵的优势:

Binary classification task – Linear discriminant analysis
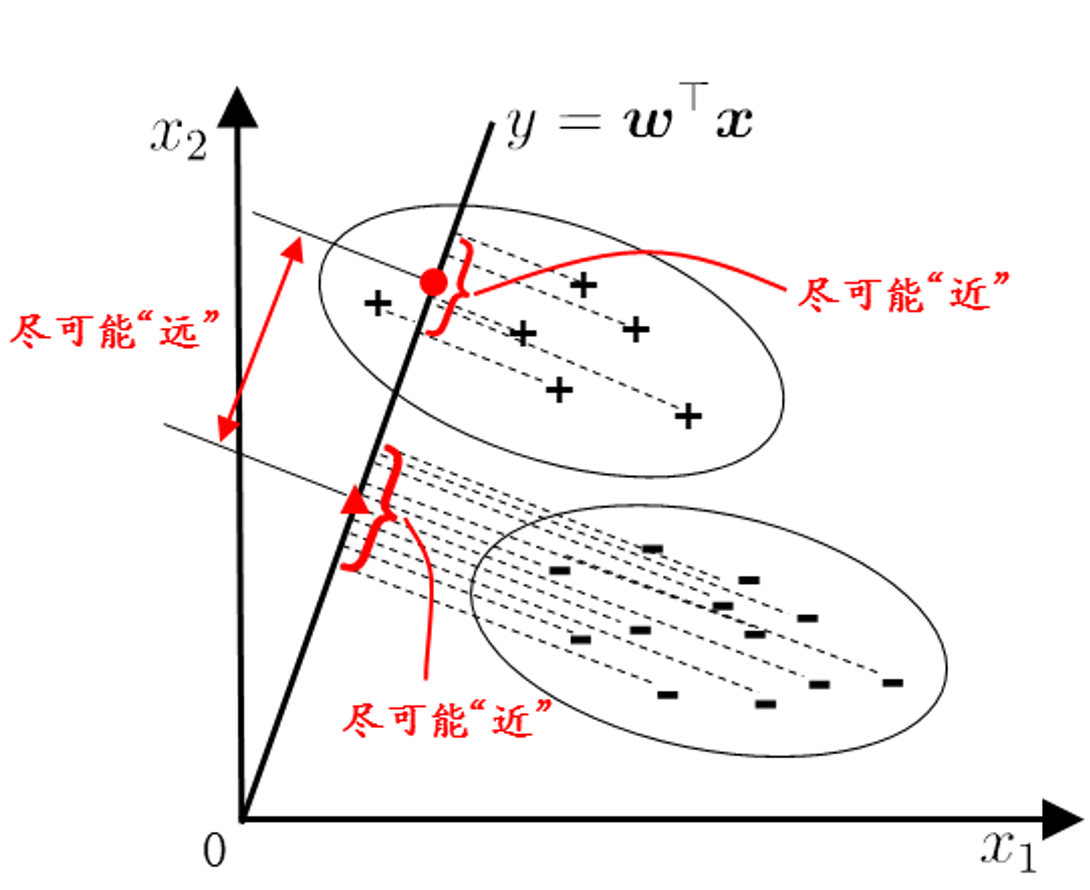
原理:
- 类间的距离尽可能的远,类内的方差尽可能的小。
原理投射的数学公式:
LDA 的优化目标可以表示为最大化:
其中:
分子:类间距离
表示两个类别中心投影点之间的距离,目标是让它尽可能大。
分母:类内方差
表示投影后同一类别样本的方差,目标是让它尽可能小。
其他关键变量说明:

调整投影向量 使类间距离最大

- 求最小化的
所以我们只用最小化 :
使用拉格朗日定理计算出:
可以看出,
所以:
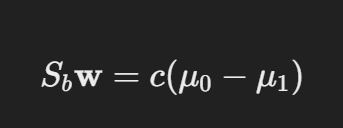
所以:

求解

泛化
全局散度:
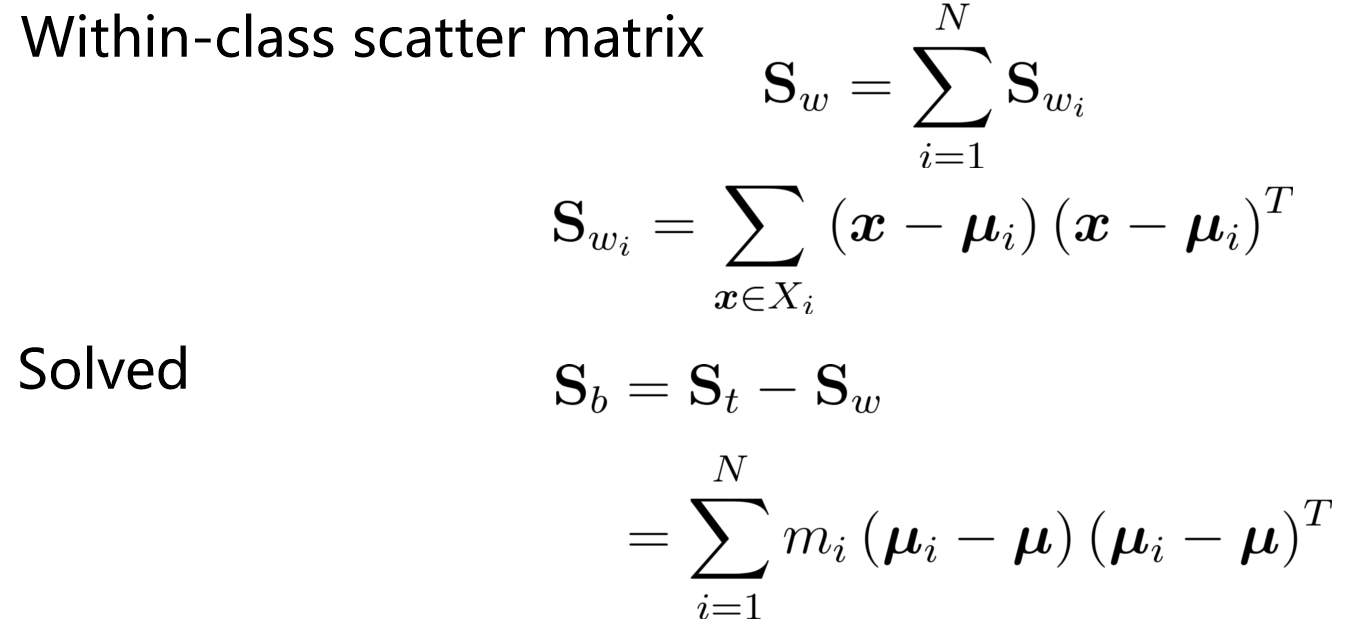
- 多分类 LDA 将样本投射到 N-1 维空间中。N-1 通常远小于数据的原始属性数。因此,LDA 也被视为一种有监督的降维技术。
Multi-classification Learning
常用的拆分策略:
- One-vs-One (OvO):
- 针对每两个类别训练一个二分类器。
- 需要训练N(N-1)/2个二分类器,其中 N 是类别总数。
- One-vs-Rest (OvR):
- 每个类别与所有其他类别对比,训练一个二分类器。
- 共需要训练 N 个二分类器。
- Many-vs-Many (MvM):
- 将多个类别同时分成两组,训练二分类器进行对比。
预测阶段:
OVO
- New samples are submitted to all classifiers for prediction
- N(N-1)/2 classification results
- Voting produces the final classification results
- The most predicted category is the final category
Testing Phase(测试阶段):
- 输入新样本:
- 将样本输入到所有N(N-1)/2 个二分类器中进行预测。
- 投票机制:
- 每个二分类器预测出一个类别,所有的预测结果通过“投票”进行统计。
- 最终被预测次数最多的类别被选为最终分类结果。
OVR
任务分裂阶段(Task Splitting)
- 方法:
- 将其中一个类别作为正类,其余所有类别合并作为负类。
- 对每个类别执行此操作,总共需要训练 N 个二分类器(其中 N 是类别的总数)。
- 学习过程:
- 每个类别对应一个二分类器,将其作为正类,其它类别作为负类。
测试阶段(Testing Phase)
- 新样本预测:
- 将新样本输入所有 N 个二分类器,得到 N 个分类结果。
- 分类结果比较:
- 比较所有分类器的预测置信度,选择置信度最高的类别作为最终分类结果。
图解
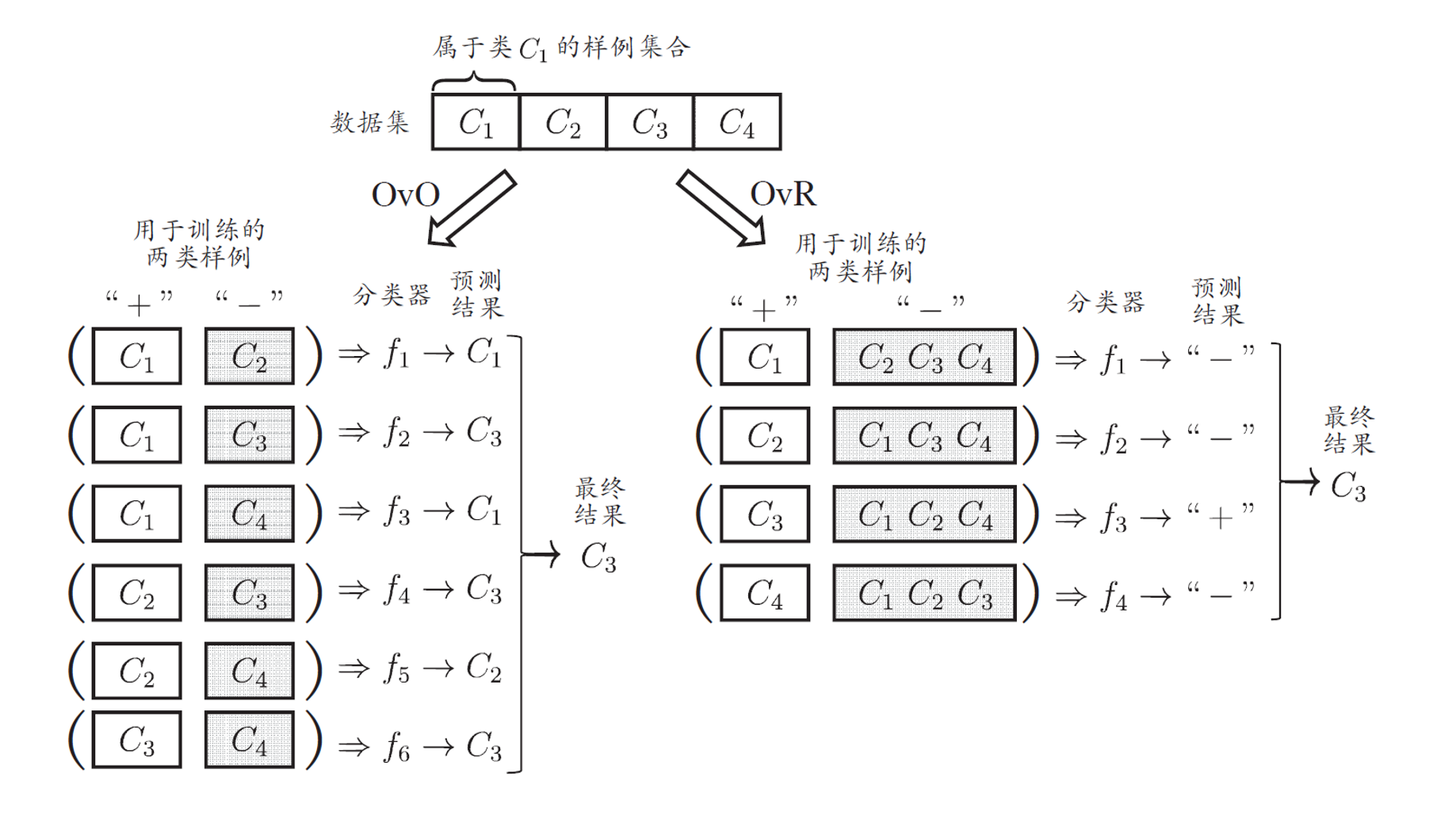
OVO and OVR 的优劣
OVO:
Training $ N(N-1)/2$ classifiers, large storage overhead and test time
Only two classes of samples are used for training, so the training time is short
OVR:
- Training N classifiers with low storage overhead and test time
- All training examples are used for training, and the training time is long
MVM
分类:
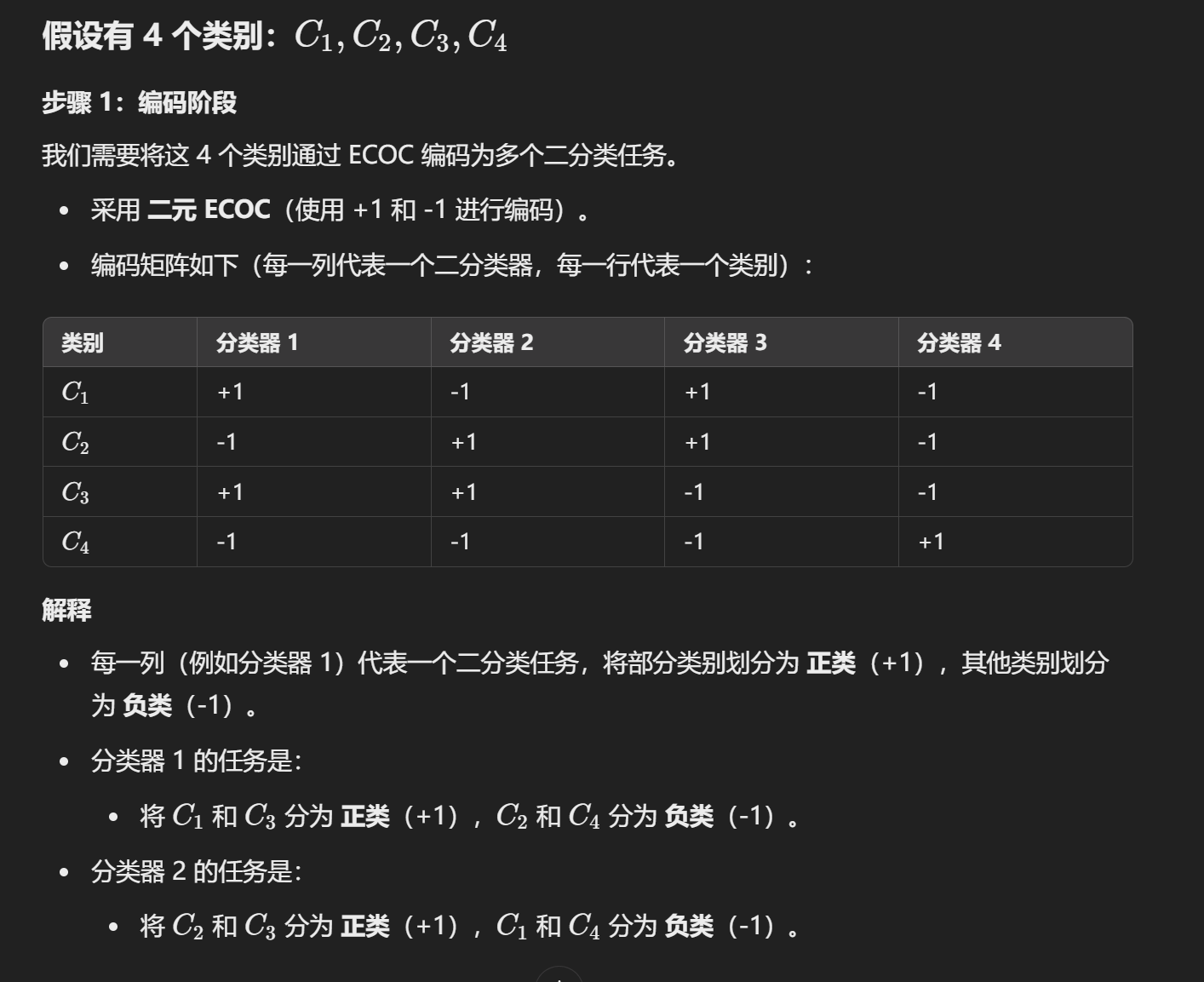
解码:
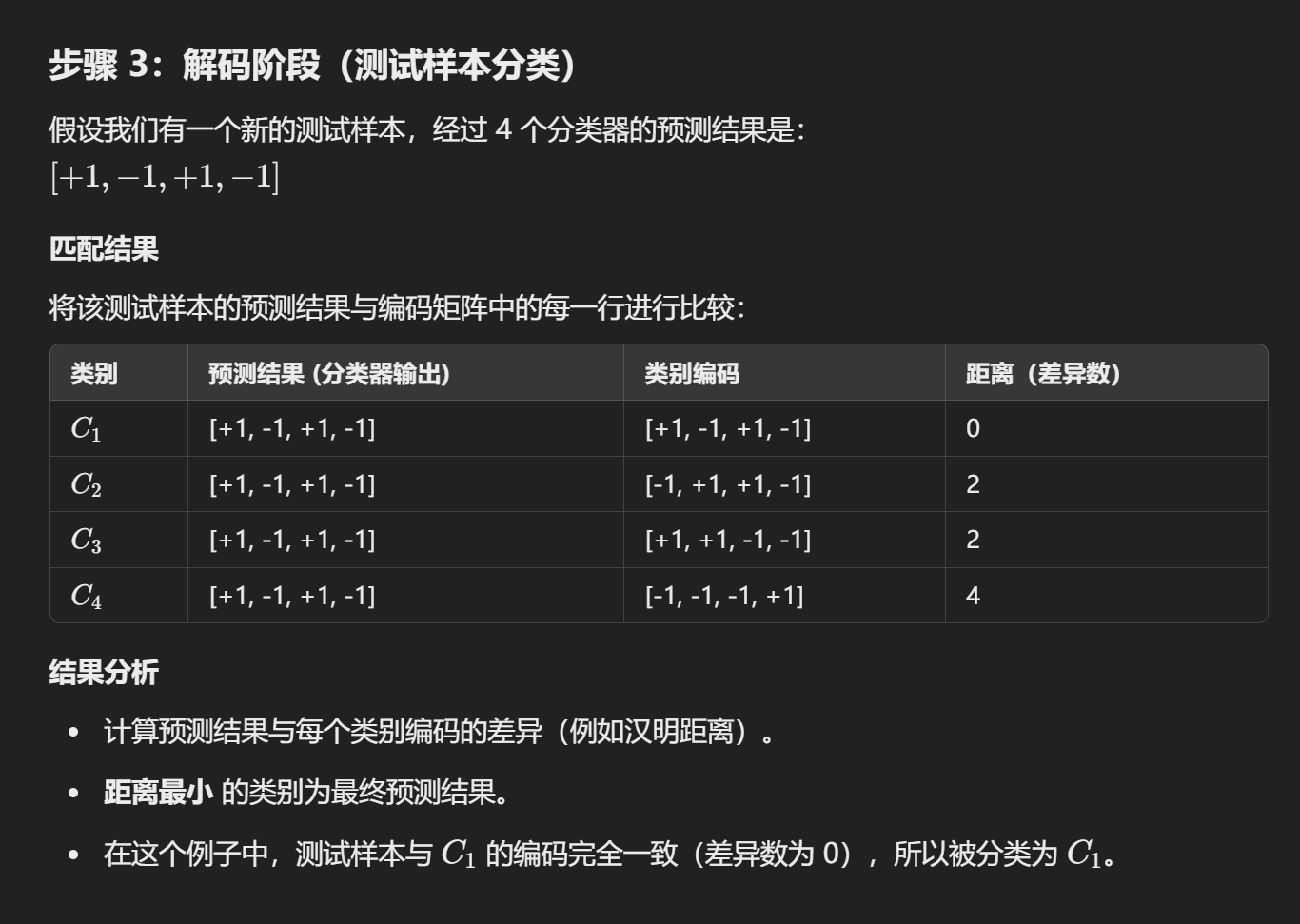
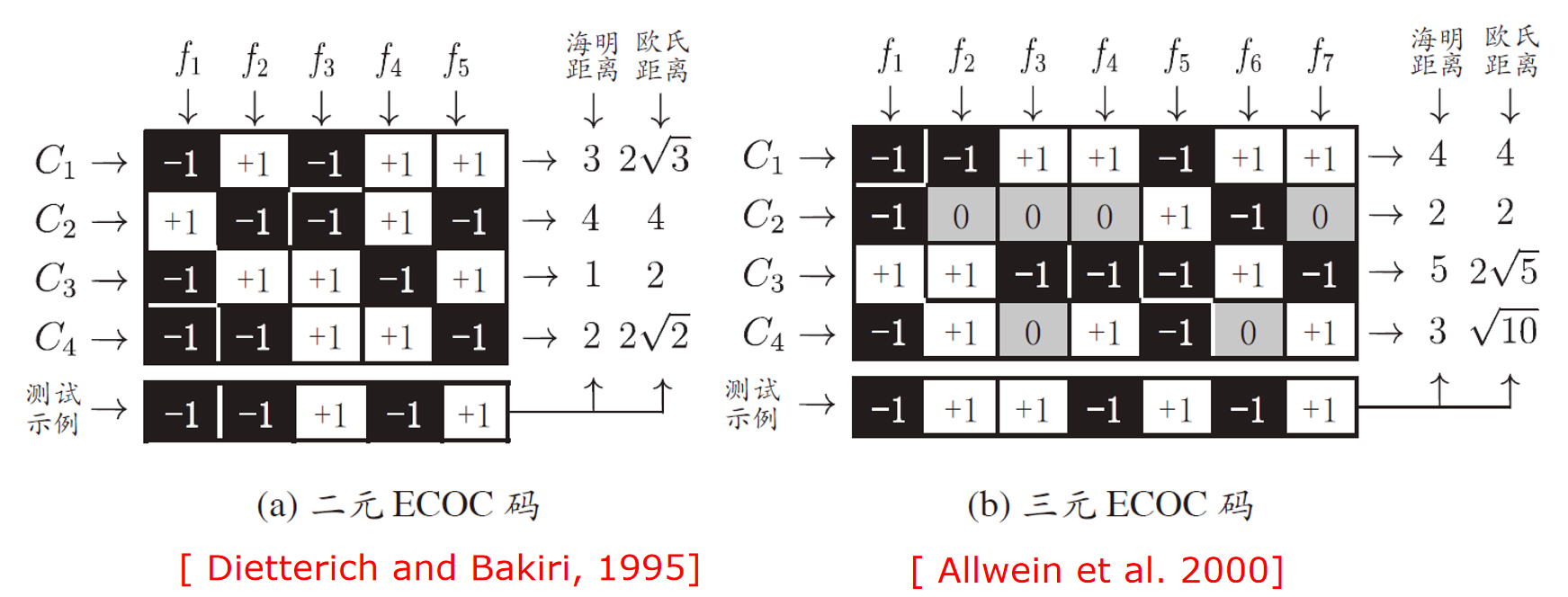
更复杂的解码过程:
- ECOC 编码对分类器错误有一定的容错和纠错能力。编码越长,纠错能力越强。
- 对于相同长度的编码,理论上任何两类之间的距离越大,纠错能力就越强。
类别不平衡
类别不平衡问题影响模型的训练和预测表现,特别是对正类样本的识别率。解决类别不平衡的常见策略包括:
- 欠采样:减少负类样本。
- 过采样:增加正类样本。
- 阈值调整:通过修改决策阈值来平衡类别预测的结果。
