机器学习第2章
Mathematical Foundation
linear algebra 线性代数
- Vector(数值的有序列表),
- matrices(二维数组,每个元素由两个索引定位),
- Scalar(标量,单一的数值)
- 张量 (Tensor): 拓展到更高维的数组。
Basics of calculus
泰勒公式 (Taylor's Formula)。
导数 (Derivatives) 和梯度 (Gradients):
- 梯度是向量,用于表示函数的偏导数。
概率与统计基础 (Basics of Probability and Statistics)
- 概率公式 (Probability Formulas)。
- 常见分布 (Common Distributions)。
- 统计概念 (Statistics)。
范数 (Norms)
- 矩阵范数: 通过矩阵元素计算的扩展范数。
导数(Derivative)
导数表示函数值在某一点的变化率,可以通过以下公式计算
梯度 (gradient)
定义:对于多元函数
性质:
- 方向:梯度的方向是函数值变化最快的方向。
- 模长:梯度的模长表示函数值变化的最大速率。
泰勒展开(Taylor Expansion)
- 定义:用多项式函数逼近光滑函数:
矩阵微分(Matrix Differentiation)
定义:通过矩阵和向量表示多变量函数的偏导数。
形式:
标量对向量的偏导:结果是一个向量。
向量对向量的偏导:结果是一个矩阵(雅可比矩阵)。
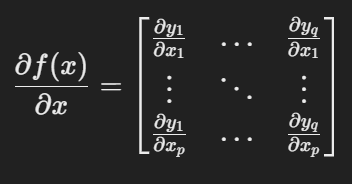
链式法则:


Classification of Machine Learning Models
Machine Learning ~= The ability to find a function
1. 统计学习
三要素
统计学习是从数据中学习模型的一种方法,核心由三部分组成:
- 模型(Model)
- 定义:假设问题可以用一个函数 f 表示,并且该函数属于某个假设空间(Hypothesis Space)。
- 目标:通过假设空间确定可用的模型类型,例如线性模型、非线性模型、生成模型或判别模型。
- 举例:
- 假设线性函数 y = kx + b 来拟合数据。
- 决定模型是监督学习模型、无监督学习模型还是强化学习模型。
- 策略(Strategy)
- 定义:选择最佳模型的标准,通常用一个目标函数或损失函数来描述。
- 目标:最小化(或最大化)目标函数,从而找到最优模型。
- 常见的策略:
- 最小化平方误差(Least Square Error)。
- 最大化似然函数(Maximum Likelihood)。
- 举例:使用均方误差
- 算法(Algorithm)
- 定义:实现优化目标的具体计算方法,用于求解模型参数。
- 目标:在假设空间中找到使损失函数最优的模型。
- 常见算法:
- 梯度下降(Gradient Descent)。
- 牛顿法。
- 举例:通过梯度下降优化
模型的分类
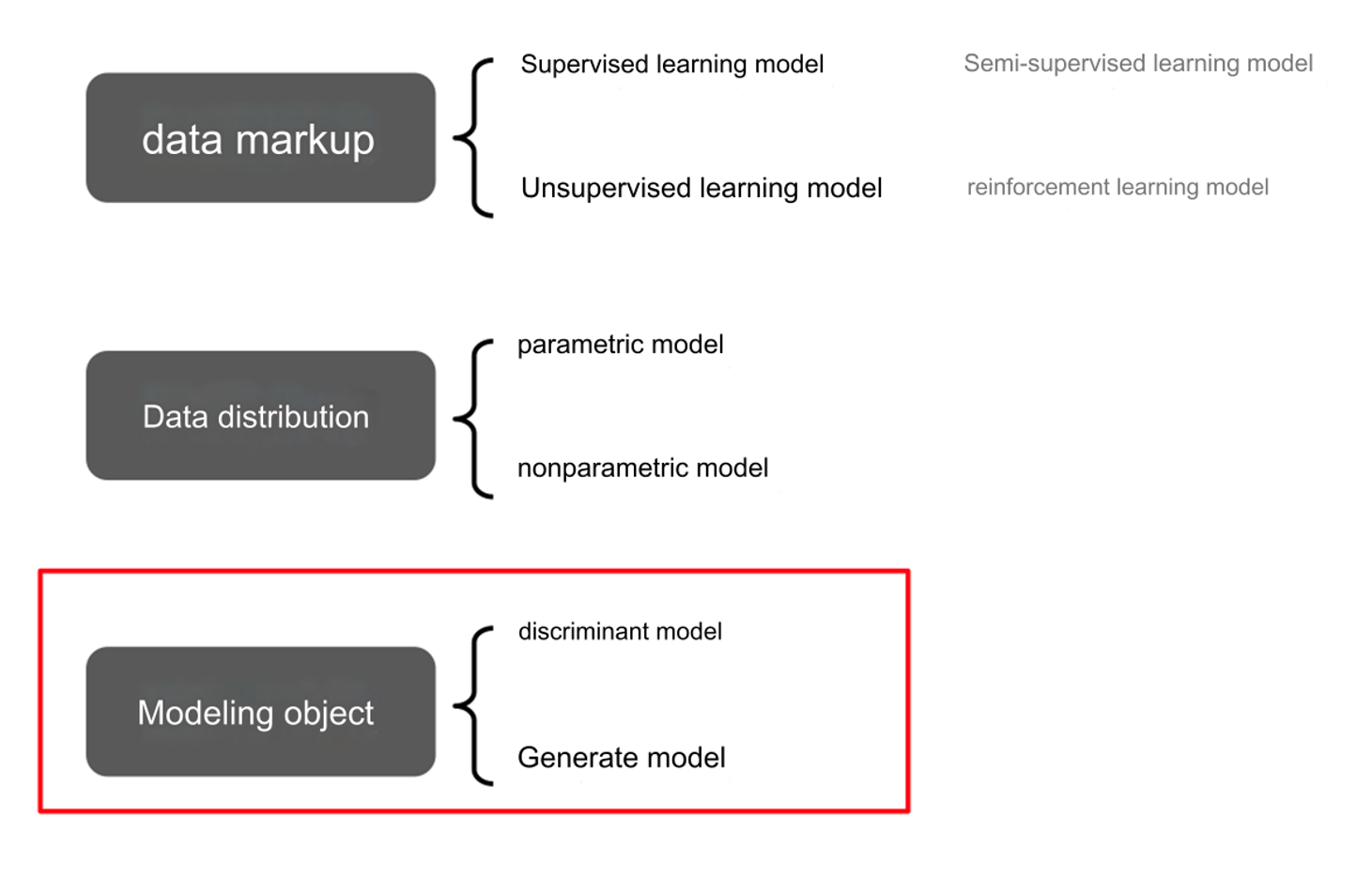
数据标注(Data Markup):
- 监督学习:需要有标签的数据集。
- 无监督学习:数据没有标签。
- 半监督学习:部分数据有标签。
- 强化学习:通过奖励信号学习。
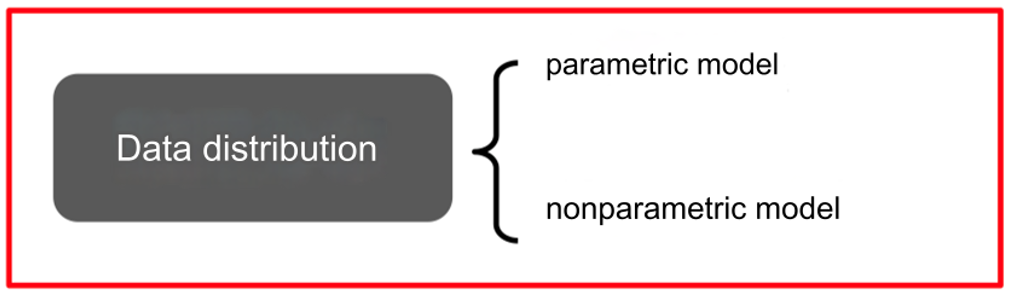
数据分布(Data Distribution):
- 参数模型(Parametric Model):假设数据分布符合某种参数化形式。
- 非参数模型(Nonparametric Model):不对数据分布做明确假设。
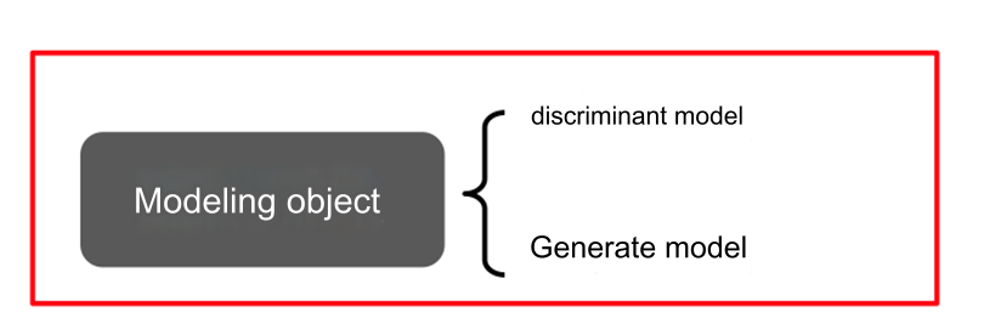
基于数据的建模对象:
- 判别模型(Discriminant Model):直接学习输入与输出的条件概率。
- 生成模型(Generate Model):学习数据的联合分布。
2. Supervised Learning
监督学习是一种通过已有的标注数据(训练数据)来训练模型的方法,用于从输入到输出之间建立映射关系。
目标:
- 寻找一个“最佳函数”
,使得对于输入数据 x,模型 能够输出正确的标签 y。
步骤

详情

Summary

3. Supervised & Unsupervised
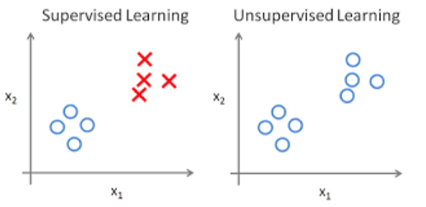
数据特性:
监督学习:
训练数据包含标签(Labeled Data)。
每个样本都有已知的输入和对应的输出(如图片的类别“猫”或“狗”)。
无监督学习:
- 训练数据不包含标签(Unlabeled Data)。
- 仅有输入数据,没有对应的输出。
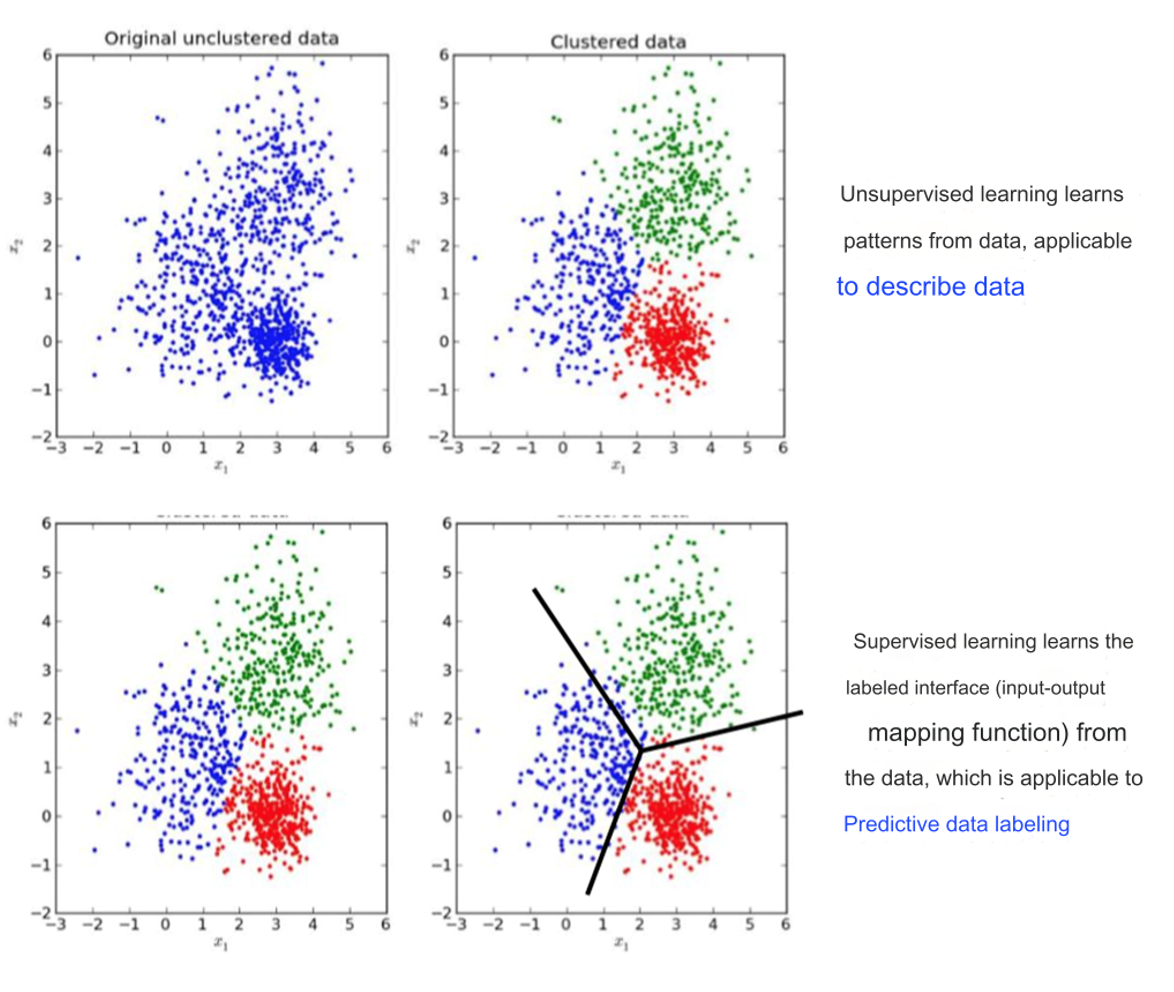
目标:
- 监督学习:
- 学习输入 x 和输出 y 之间的映射关系 f(x)。
- 给定带标签的图片数据,模型学习如何从输入的图片预测正确的标签。
- Supervised learning learns the labeled interface (input-output mapping function) from the data, which is applicable to Predictive data labeling.
- 无监督学习:
- 发现数据的内在结构、模式或分布。
- Unsupervised learning learns patterns from data, applicable to describe data.
- 常见任务:
- 聚类(如K均值聚类)。
- 降维(如主成分分析PCA)。
4. Semi-supervised learning
数据长啥样:
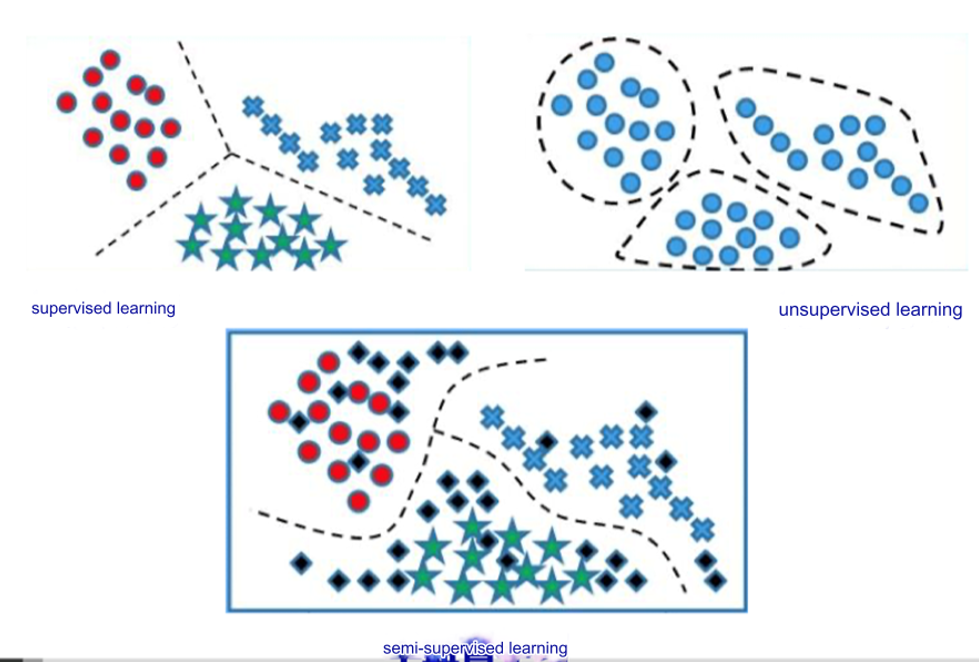
- 数据特性:
- 部分数据有标签,部分数据没有标签。
- 目标:
- 结合有标签和无标签数据的优势,提高模型的预测能力。
- 示例:
- 用少量标注过的猫狗图片和大量未标注的图片,训练分类模型。
怎么处理未标注数据?
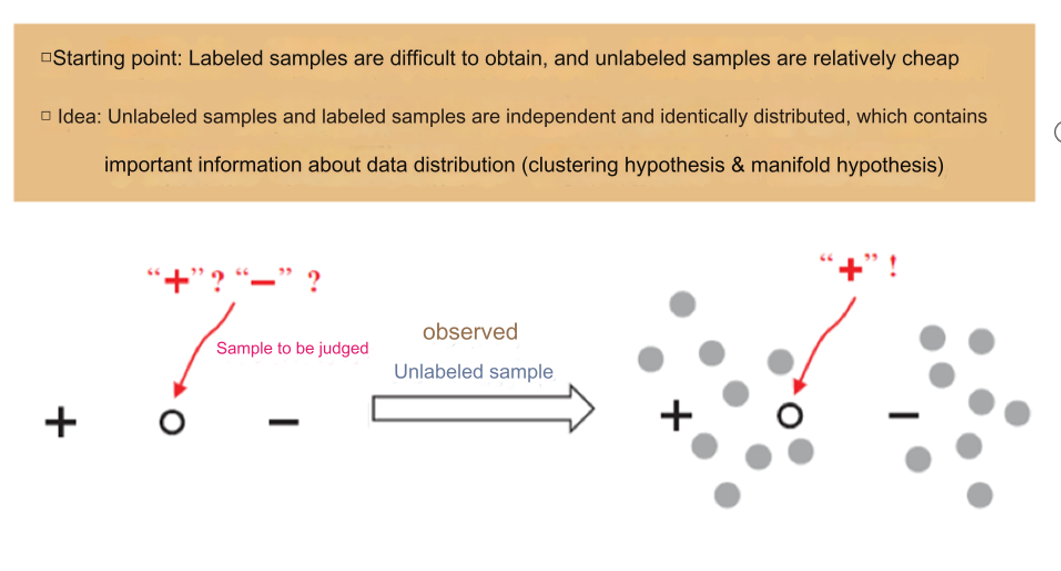
左侧:
- “Sample to be judged”(待判断的样本):
- 图中用圆圈表示一个未标注样本,需要预测它的标签。
- 标签可能是 "+"或 "−"。
- 通过利用标注数据 "+" 和 "−",结合未标注样本的信息,预测该样本的标签。
右侧:
- 未标注样本通过学习数据分布的模式,逐步被分类:
- 将未标注样本与标注样本相似的部分分配到对应的类别。
- 最终,“待判断样本”被标记为 "+"。
半监督学习的假设
- 聚类假设(Clustering Hypothesis):
- 样本可以自然地聚类到几个簇,每个簇对应一个类别。
- 示例:在二维图中,相邻的点更可能属于同一类别。
- 流形假设(Manifold Hypothesis):
- 数据分布在低维的流形结构上,即使数据本身处于高维空间。
- 通过找到流形结构,可以更好地理解数据分布。
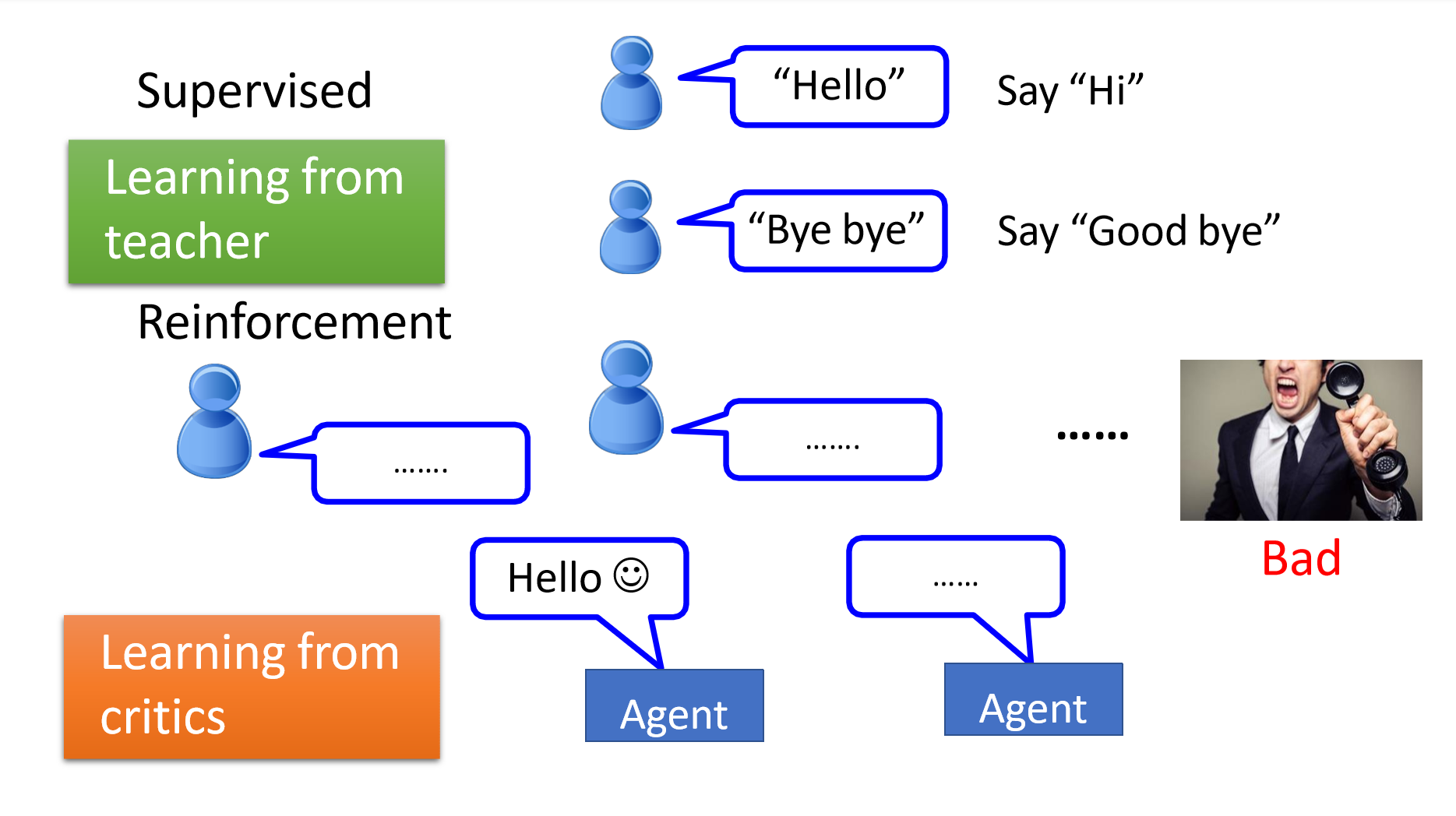
5. 强化学习模型(Reinforcement Learning)
- 数据特性:
- 数据没有明确的标签(Unlabeled Data)。
- 通过与环境交互,模型获得奖励信号(Reward Feedback)来指导学习。
- 目标:
- 学习一个策略,使得在特定环境下,累积奖励最大化。
- 反馈机制:
- 强化学习通过奖励和惩罚信号评估行为的好坏,而不是直接告知正确答案。
类比描述:Hotter or Colder
- 强化学习类似于“热与冷”的游戏:
- 当接近目标时,模型获得“热”的正反馈;
- 当远离目标时,模型获得“冷”的负反馈。
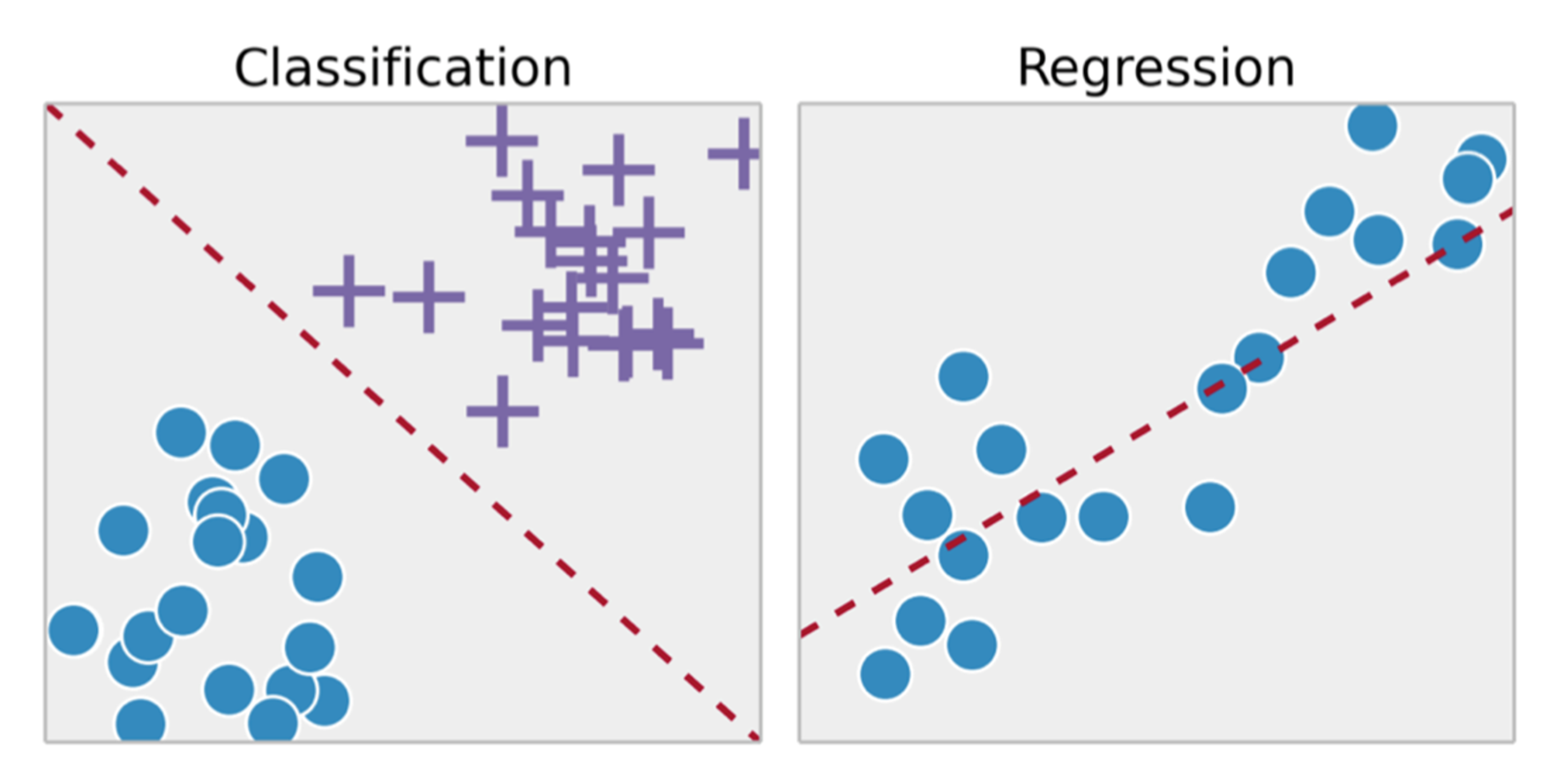
5. classification & Regression
6. Classification mode
二分类(Binary Classification)
- 定义:
- 一个对象只属于两个可能的类别之一。
- 类别是互斥的(mutually exclusive),即一个对象只能属于其中一个类别。
- 示例:
- 判断一封邮件是“垃圾邮件”还是“正常邮件”。
- 医学诊断中,判断患者是否患病。
多分类(Multi-class Classification)

- 定义:
- 一个对象在多个可能的类别中只属于一个类别。
- 类别仍是互斥的。
- 示例:
- 图像分类:将图片分为“猫”、“狗”或“鸟”。
- 学生考试成绩的等级分类:优、良、中、差。
多标签分类(Multi-label Classification)
- 定义:
- 一个对象可以同时属于多个类别。
- 类别之间不互斥,可以相关联。
- 示例:
- 音乐推荐:一首歌可以同时属于“流行”和“摇滚”类别。
- 图像标签:一张图片可以同时标记为“狗”和“草地”。
7. Self-Supervised Learning
概念
- 自监督学习通过构造辅助任务(Auxiliary Tasks),从大量无标签数据中生成监督信号。
- 本质上是一种特殊的无监督学习,但通过自定义的方式生成伪标签,使其模拟监督学习。
Self-supervised learning uses auxiliary tasks (pretext) to artificially construct supervisory information from large-scale unsupervised data and learn valuable feature representations.
自监督学习利用辅助任务(预设任务)从大规模无监督数据中人为构建监督信息,并学习有价值的特征表示。
图片内容
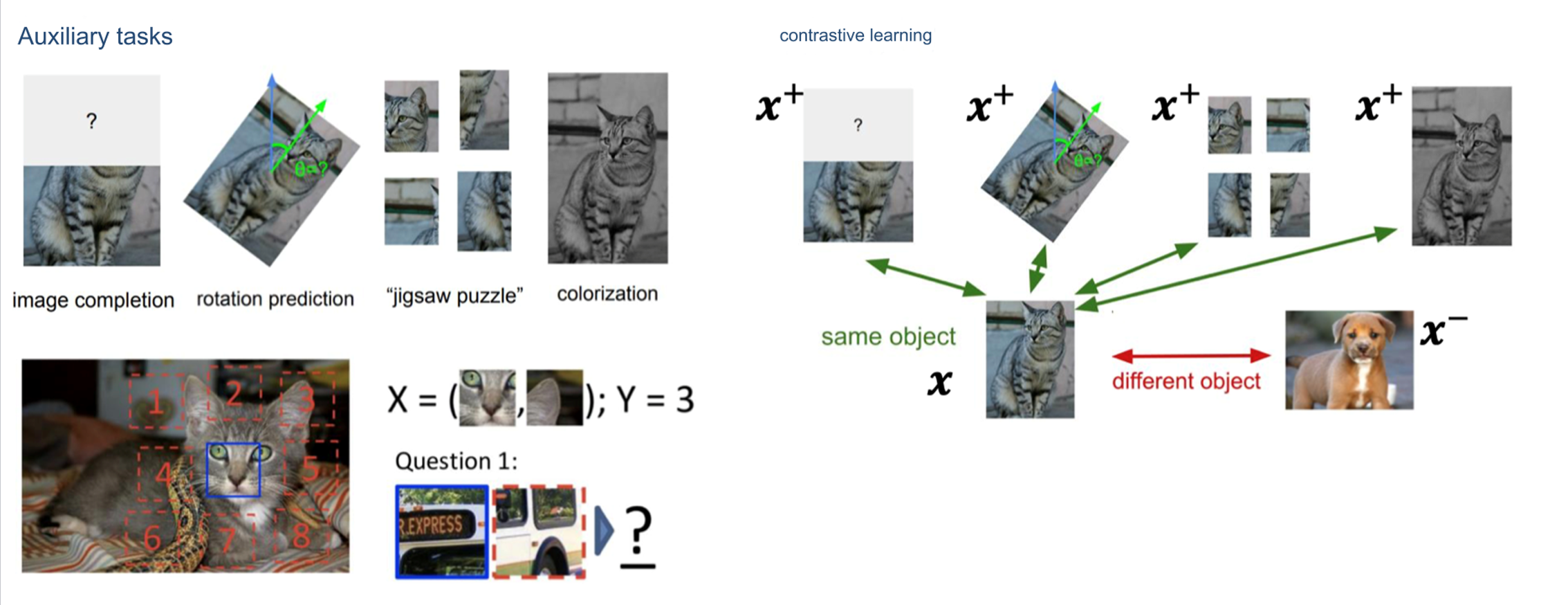
- 辅助任务(Auxiliary Tasks):
- Image completion:预测图片中缺失的部分。
- Rotation prediction:预测图片的旋转角度。
- Jigsaw puzzle:将图片分割后打乱,模型需要重新排列。
- Colorization:将黑白图片恢复为彩色。
- 对比学习(Contrastive Learning):
- 目标:
- 将同一对象的不同视图(如不同角度或数据增强后的样本)拉近。
- 将不同对象的表示分离。
- 正样本(Positive Samples):
- 来自同一对象的不同视图。
- 负样本(Negative Samples):
- 来自不同对象的数据。
- 目标:
8. 参数模型与非参数模型
Parametric model:
Assuming the data distribution, the data pattern/mapping to be solved can be characterized by a limited and fixed number of parameters.
假设数据分布,待解决的数据模式或映射可以通过有限且固定数量的参数来表征。
注
定义:
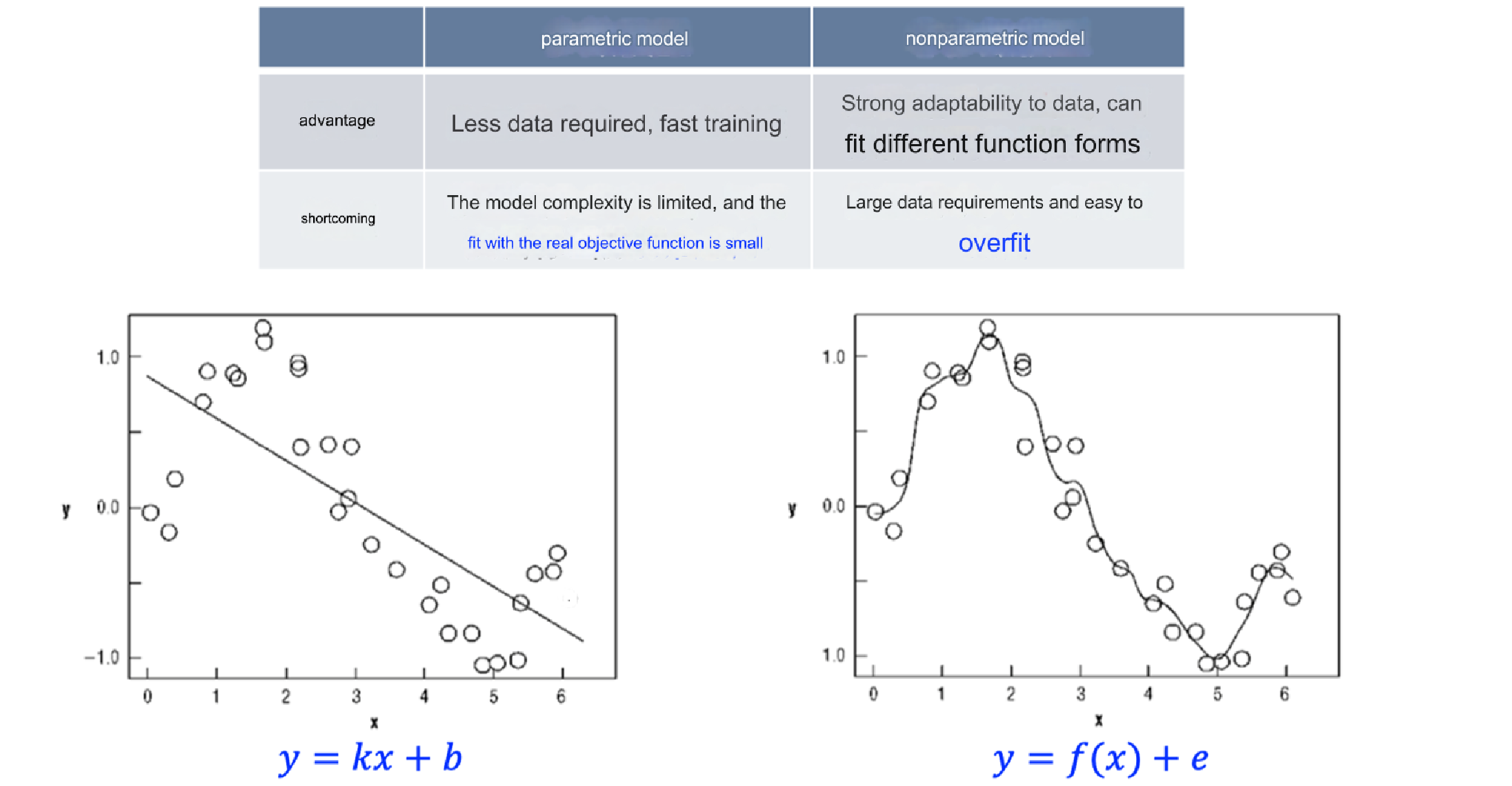
- 假设数据分布,并用有限的参数来刻画模型。
- 参数数量固定,数据量的变化不会影响模型复杂度。
特点:
- 适合数据分布已知或明确的场景。
- 模型简单,训练效率高。
例子:
- 线性回归(Linear Regression)、逻辑回归(Logistic Regression)。
Sometimes the data does not provide enough information to assume the distribution in advance, or the problem itself does not have obvious distribution characteristics.
中文翻译:
有时数据本身不足以提供足够信息来提前假设分布,或者问题本身没有明显的分布特征。
SO:
Nonparametric model:
注
- 定义:
- 不对数据分布做明确假设。
- 模型的复杂度随数据量增加而增加。
- 特点:
- 灵活,能适应复杂的数据分布。
- 计算复杂度较高。
- 例子:
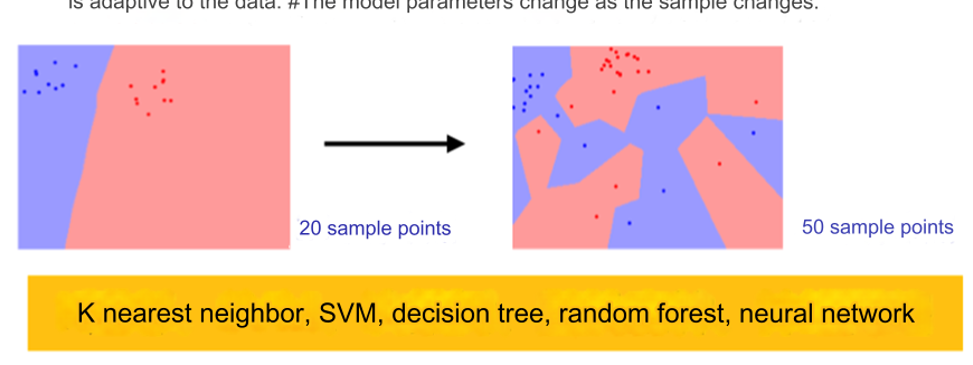
- 最近邻算法(KNN)、支持向量机(SVM)、决策树(Decision Tree)。
- 图中示例展示KNN算法:样本点的分类边界随着数据数量的变化而调整。
- 图片说明:
- 对比不同数据量下的决策边界,随着数据点增加,模型边界更加精细。
No assumptions are made about data distribution. All statistical properties of the data come from the data itself.
中文:不对数据分布做任何假设。数据的所有统计特性完全来源于数据本身。
非参数模型不会依赖于特定的数据分布假设(如正态分布、高斯分布)。
它的灵活性更高,因为模型直接从数据中提取信息,而非先验假设。
Non-parameter ≠ No parameter
- "Parameter" refers to the parameters of the data distribution, not the parameters of the model.
- The space-time complexity of non-parametric models is generally much greater than that of parametric models.
- The #model parameters of the parametric model are fixed, while the non-parametric model is adaptive to the data. #The model parameters change as the sample changes.
中文翻译:
非参数 ≠ 无参数
- "参数"指的是数据分布的参数,而非模型的参数。
- 非参数模型的时空复杂度通常远高于参数模型。
- 参数模型的模型参数是固定的,而非参数模型的参数随着样本的变化而变化。
对比
9. Generative & discriminative
定义:
Generative:
Modeling the joint distribution P(X, Y) of input X and output Y.
- 生成模型的目标是建模输入 X 和输出 Y 的联合分布
- 它尝试从数据中学习输入和输出的全部信息,并通过联合分布推断条件概率
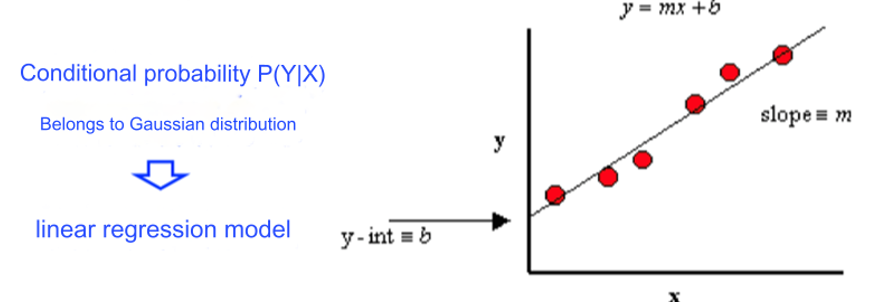
Discriminative:
Output Y under known input X.
- 判别模型直接建模条件概率 P(Y∣X),即预测给定输入 X 时输出 Y 的可能性。
- 不关心输入和输出的联合分布 P(X,Y),只专注于分类边界。
例子


generate model
Advantage:
- Provide more information (modeling marginal distribution → sampling to generate samples)
- When the sample size is large, it converges to the true distribution faster.
- Support complex training situations (unsupervised training, when there are hidden variables)
提供更多信息(边际分布建模 → 抽样生成样本)
样本量大时,收敛到真实分布的速度更快。
支持复杂的训练情况(无监督训练,当存在隐藏变量时)
Shortcoming:
- Big data requirements
- The accuracy of prediction problems is usually not as good as that of discriminative models.
大数据要求
预测问题的准确性通常不如判别模型。
理解的例子
你是侦探,要分析一封信件是好人写的还是坏人写的。
生成模型的思路是这样的:
- 你去分析好人平时写信的方式,统计出“好人用的词语概率分布”;
- 同时,你也去分析坏人写信的方式,搞清楚“坏人用的词语概率分布”;
- 当拿到新信件时,你看它的词语分布更像好人还是坏人,从而做出判断。
核心在于:生成模型希望学到“好人信”和“坏人信”的“内部规律”,用这些规律进行推断。
如果你是侦探,判别模型的思路是:
- 不管好人和坏人具体怎么写信,只关注“他们的区别是什么”。比如:
- 坏人常写“你要交钱”,好人常写“祝你好运”;
- 坏人信里没有祝福语,好人信里经常有。
- 你直接根据这些区别,找一个简单的规则(比如“是否包含‘祝你好运’”)来做判断。
核心在于:判别模型不关心“好人信”和“坏人信”的整体特点,而是直接学会“区分好人和坏人”的界限。
本质区别:
生成模型是“理解”和“模拟”数据:
- 它试图搞清楚“这个数据是怎么来的”(学习数据的生成规律)。
- 它不仅能分类,还能生成类似的数据。
例子:你看了很多好人信,可以模仿写出一封好人信;看了坏人信,也可以模仿写一封坏人信。
判别模型是“直接判断”数据:
- 它只关心“分类的正确性”,而不关心数据本身是怎么来的。
例子:你只知道某些特定词汇是好人常用的,就直接用这些词汇判断。
Xiguashu-Supplement

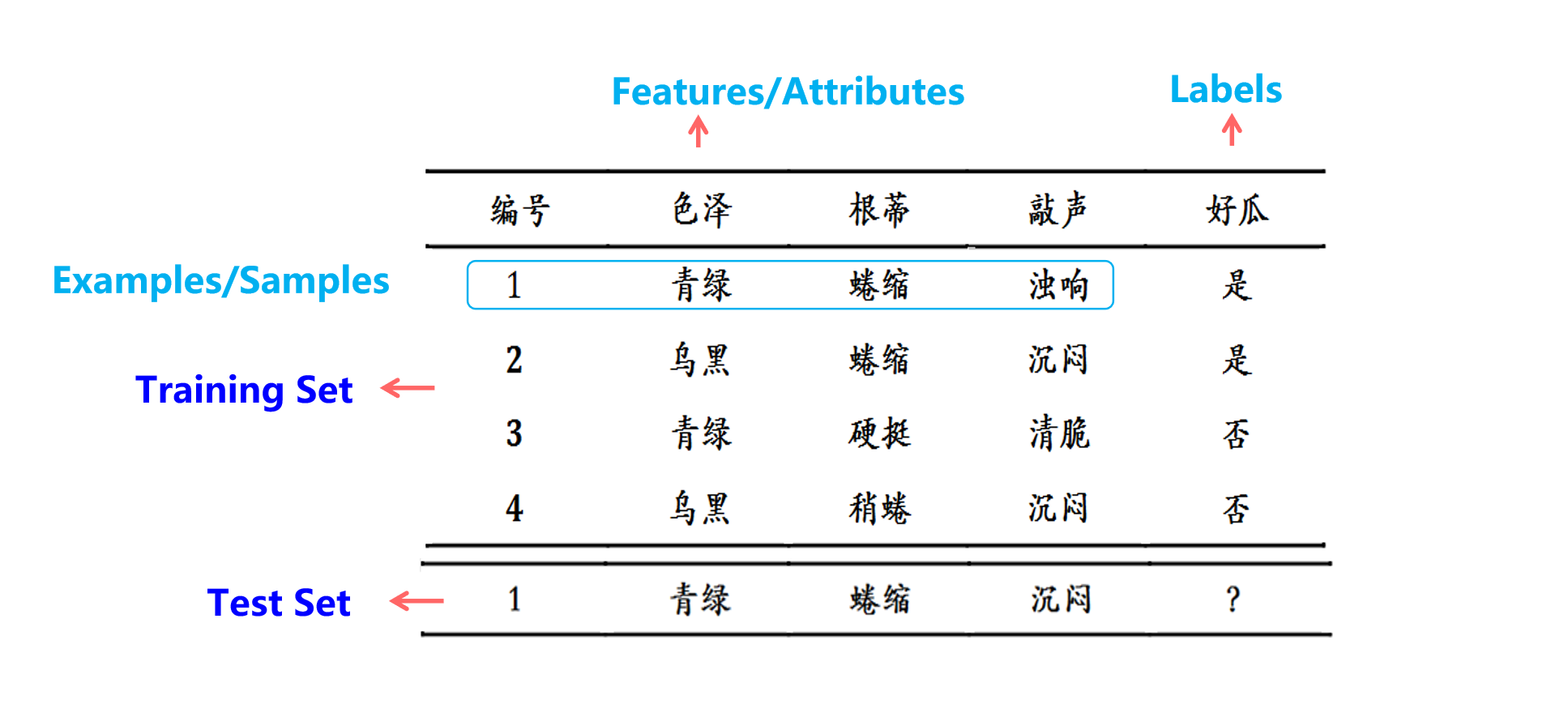
1. what is data?
2. Generalization Ability
机器学习的目标是使得学到的模型能很好的适用于“新样本”,而不仅仅是训练集合,我们称模型适用于新样本的能力为泛化(generalization)能力。
独立同分布的样本意味着:
- 它们彼此独立。
- 它们遵循同一个分布。
通常假设样本空间中的样本服从一个未知分布D,样本从这个分布中独立获得,即“独立同分布”(i.i.d)。一般而言训练样本越多越有可能通过学习获得强泛化能力的模型。
3. Hypothesis Space

- 每个属性有多种可能的取值:
- 色泽:青绿、乌黑
- 根蒂:蜷缩、硬挺、稍蜷
- 敲声:沉闷、清脆、嘭响
- 假设空间大小是所有属性取值组合的数量:假设空间大小 = 色泽的可能取值 × 根蒂的可能取值 × 敲声的可能取值 + 1(空假设)
- 在图中: 假设空间大小 = 2 × 3 × 3 + 1 = 19
4. Inductive Preference
假设空间中有多个与训练集一致的假设,但它们对 (色泽=青绿;根蒂=蜷缩;敲声=沉闷) 的瓜会预测出不同的结果。
- 第一种假设:只关注“根蒂=蜷缩”,认为是好瓜。
- 第二种假设:关注“敲声=沉闷”,认为是坏瓜。
- 第三种假设:关注“色泽=青绿”,认为是坏瓜。
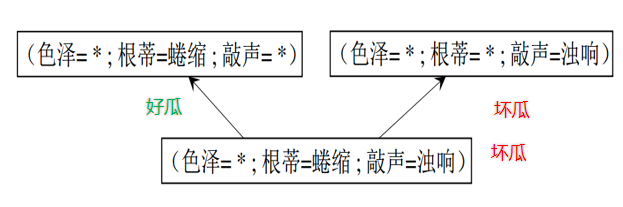
将会选择哪一个结果??
学习过程中对某种类型假设的偏好称为“归纳偏好”(Inductive Preference)。
The preference for a certain type of hypothesis during learning is called inductive preference
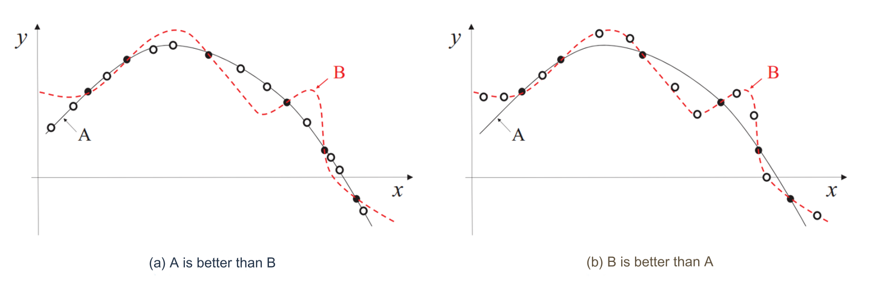
图中曲线 A 和 B 都符合训练数据点,但 B 比 A 更复杂。
直观上,我们倾向于选择较简单的曲线 A。
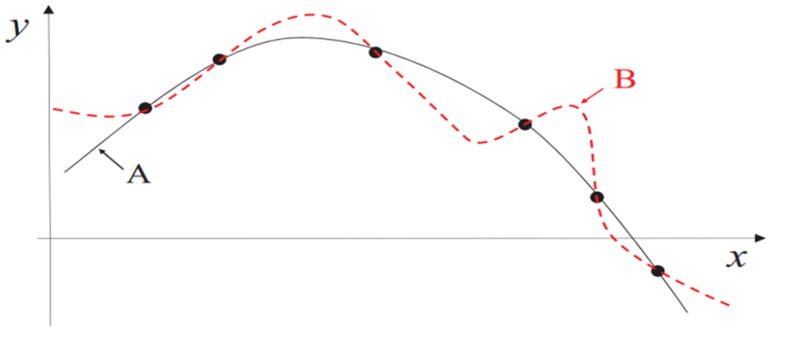
假设过于复杂可能导致“过拟合”,即它只能很好地解释训练集,却无法处理新数据(B曲线)。而简单假设则更具“泛化能力”(A曲线)。
5. NoFreeLunch
如果某个算法 A 在某些问题上比另一个算法 B 更好,那么一定存在其他问题使得 B 比 A 更好。
简而言之:没有单一的“万能”算法适用于所有问题。