机器学习第6章

Neron model

1. 模型的运行流程

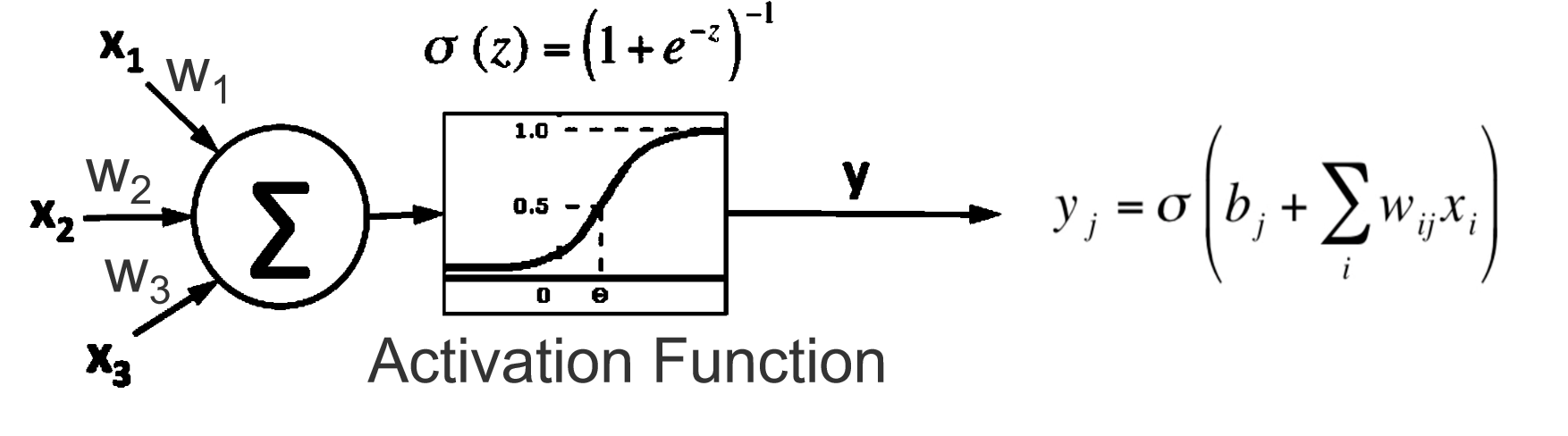
• 接收输入信号：多个输入 xix_ixi 通过加权连接传入神经元。
• 加权求和：输入信号与权重相乘后相加，并加上偏置项 $b_j$。
• 激活函数处理：加权和 z 通过激活函数 $\sigma (z)$ 进行非线性变换。
• 输出信号：生成的输出 $y_j$ 被送到下一层神经元或输出层。

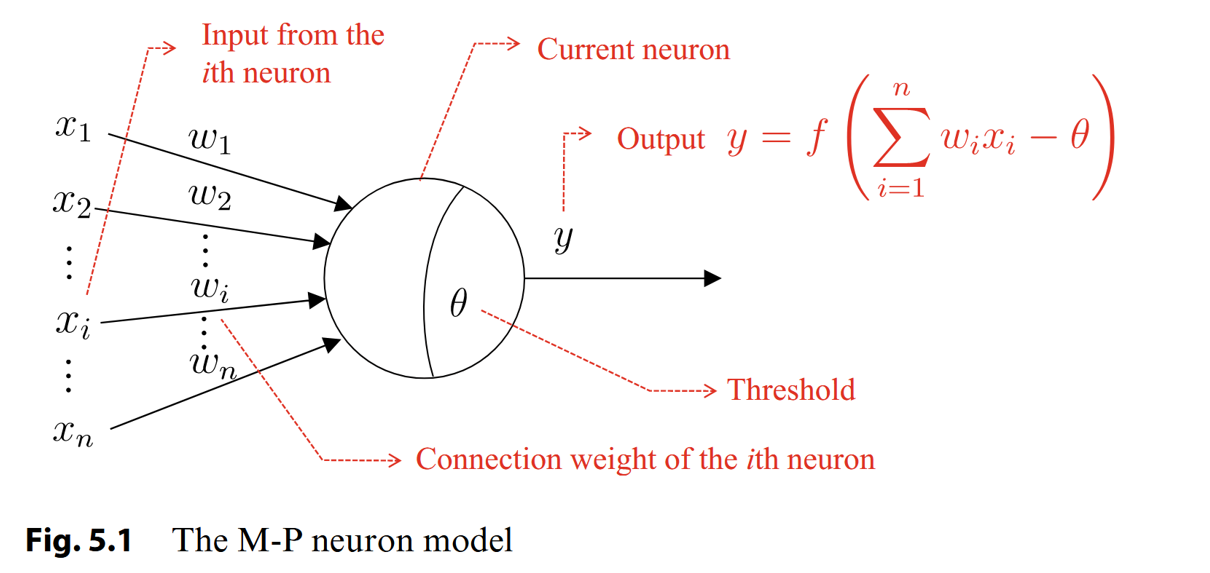
2. M-P neron model

详情

3. 激活函数

作用：把得到的加权和变成特定的输出。以下介绍两种常见的激活函数。

激活函数用于引入非线性，使神经网络能够处理复杂问题。

Step Function

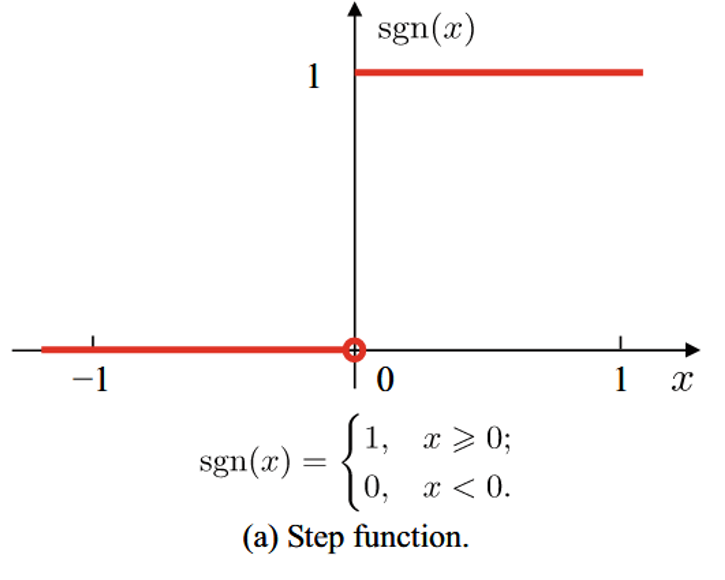
作用：当输入 $x$ 超过某个阈值时，输出为 $1$（激活）；否则输出为 $0$（未激活）。

缺点： 不连续，非平滑，无法用于梯度下降优化。

Sigmoid

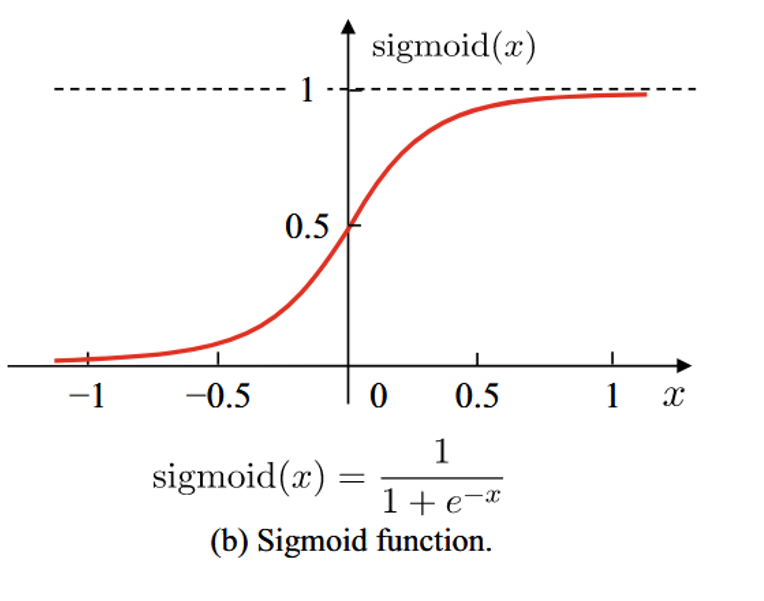
作用：将输入 x 映射到 0 到 1 之间的连续范围，平滑且可导，适合用于二分类问题。

特点：

• 当输入很大或很小时，输出趋近于 1 或 0。
• 中间值 0 附近变化较大，输出接近 0.5。

Perceptron

感知器是一种二元分类器，由两层神经元组成。输入层接收外部信号并将其传输到输出层，输出层是一个 M-P 神经元。(阈值逻辑单元）

逻辑判断

通过输出层的输出来进行逻辑判断

学习 w 和 $\theta$

权重更新由以下公式给出：

• $\eta$：学习率，控制权重更新的步长，通常取 η∈(0,1)\eta \in (0,1)η∈(0,1)。
• $y-\hat{y}$：真实值与预测值之间的误差。
• $x_i$：输入特征对应的值。

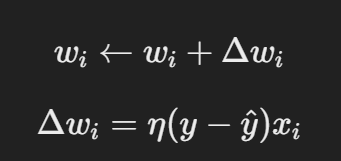
损失函数和梯度下降

• 损失函数：最小化输出误差的平方和：

​ $L=(y-\hat{y}{)}^2$

• 梯度计算：对权重求导，更新方向与负梯度一致：

​ $\frac{\partial L}{\partial w_1}=(y-\hat{y})(-1)f^{\prime }(x_1)$

​ $w_1=w_1-\eta \frac{\partial L}{\partial w_1}$

单层感知器处理逻辑判断

单层神经元，输入为 [x1;x2]（输入层不包括在层数中），使用阶跃激活函数。

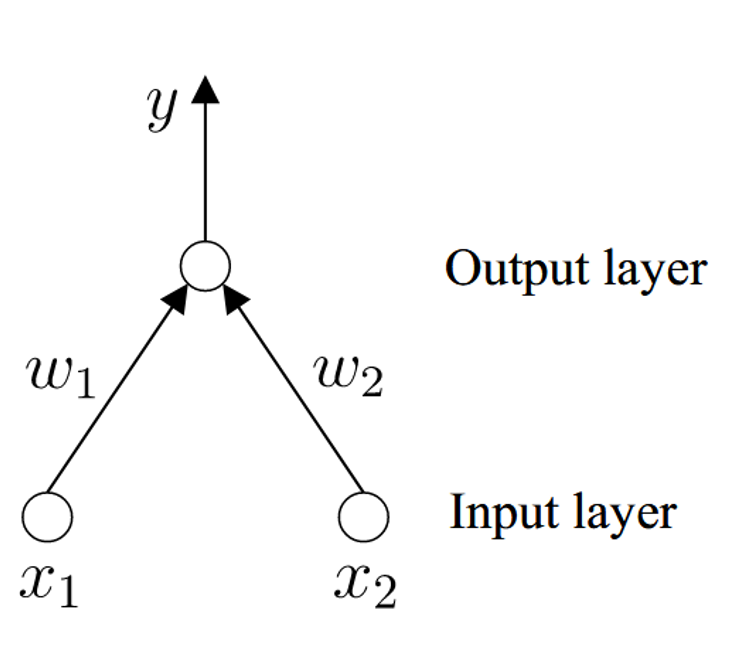
只有一个神经元能够进行判断。

也意味着只有一个激活函数能够分割坐标轴….

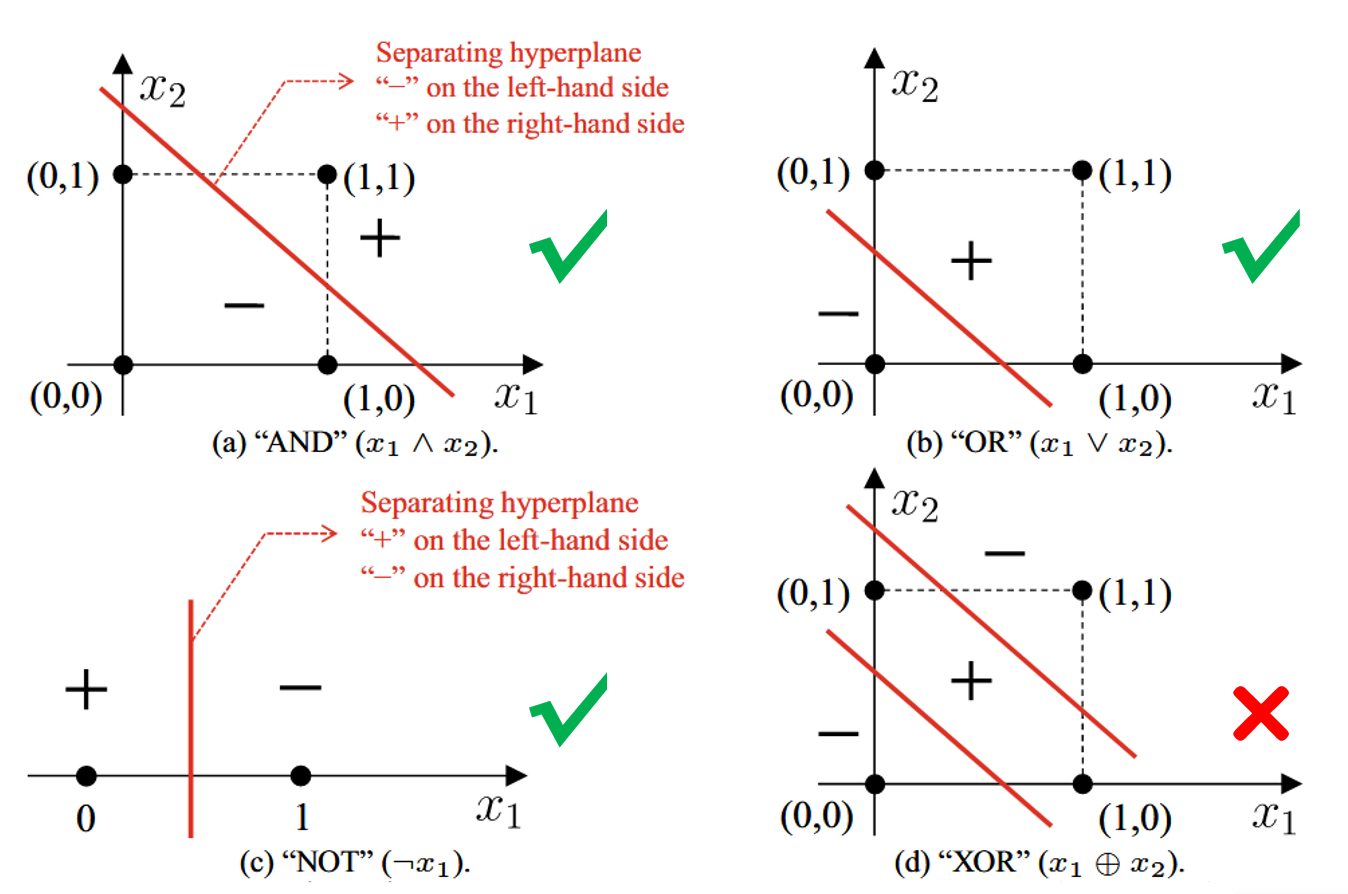
“AND” 需要 $x_1$ 和 $x_2$ 都为 1 的时候才为正，一条线就可以把 $(1,1)$ 和其他情况分割；

“OR” 需要 $x_1$ 和 $x_2$ 任意一个为 1 的时候为正，一条线就可以把 $(1,1)(0,1)(1,0)$ 和其他情况分割；

“NOT” 需要 $x_1$ 为 0 就可以输出 1，一条线就可以把横轴上的 0 和 1 分开；

“XOR” 需要 $x_1\ne x_2$ 才可以输出 1，一条线无法将 $(0,0)$ 和 $(1,1)$ 和其他坐标分开！单层感知器无法作用于 “XOR”

Two-layer perceptron

solves the "XOR" problem

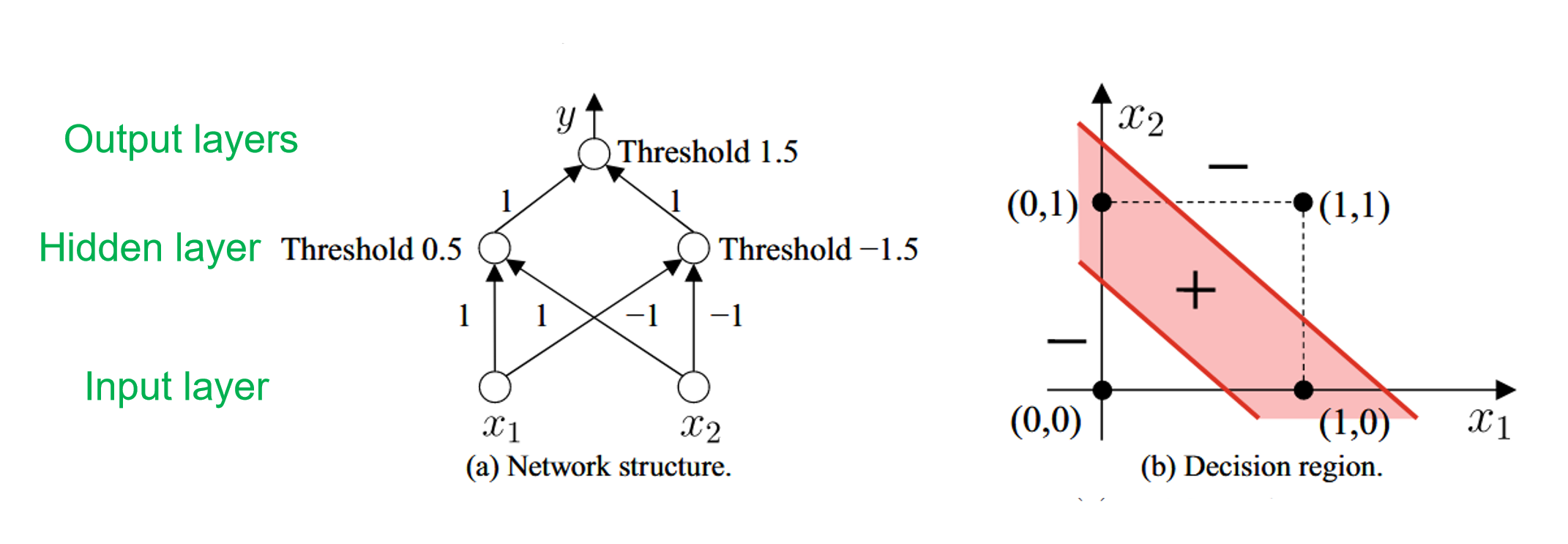
• 参数设置：

  总共要经历三层参数：（在上图也能体现）

  

一个实例

A Simple Neural Network

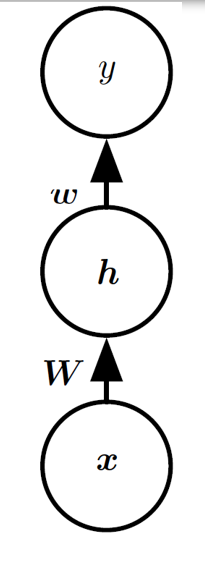
• 参数设置：

  • 权重矩阵 W 为 $\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]$。

  • 偏置向量 c 为 $\left[\begin{array}{c}0\\ -1\end{array}\right]$。

  • 第二层权重向量 w 为 $\left[\begin{array}{c}1\\ -2\end{array}\right]$。

  • 偏置 $b=0$。

  • 实战步骤：

  

• 映射图像：（怎么一条线就解决 XOR 问题？）

  

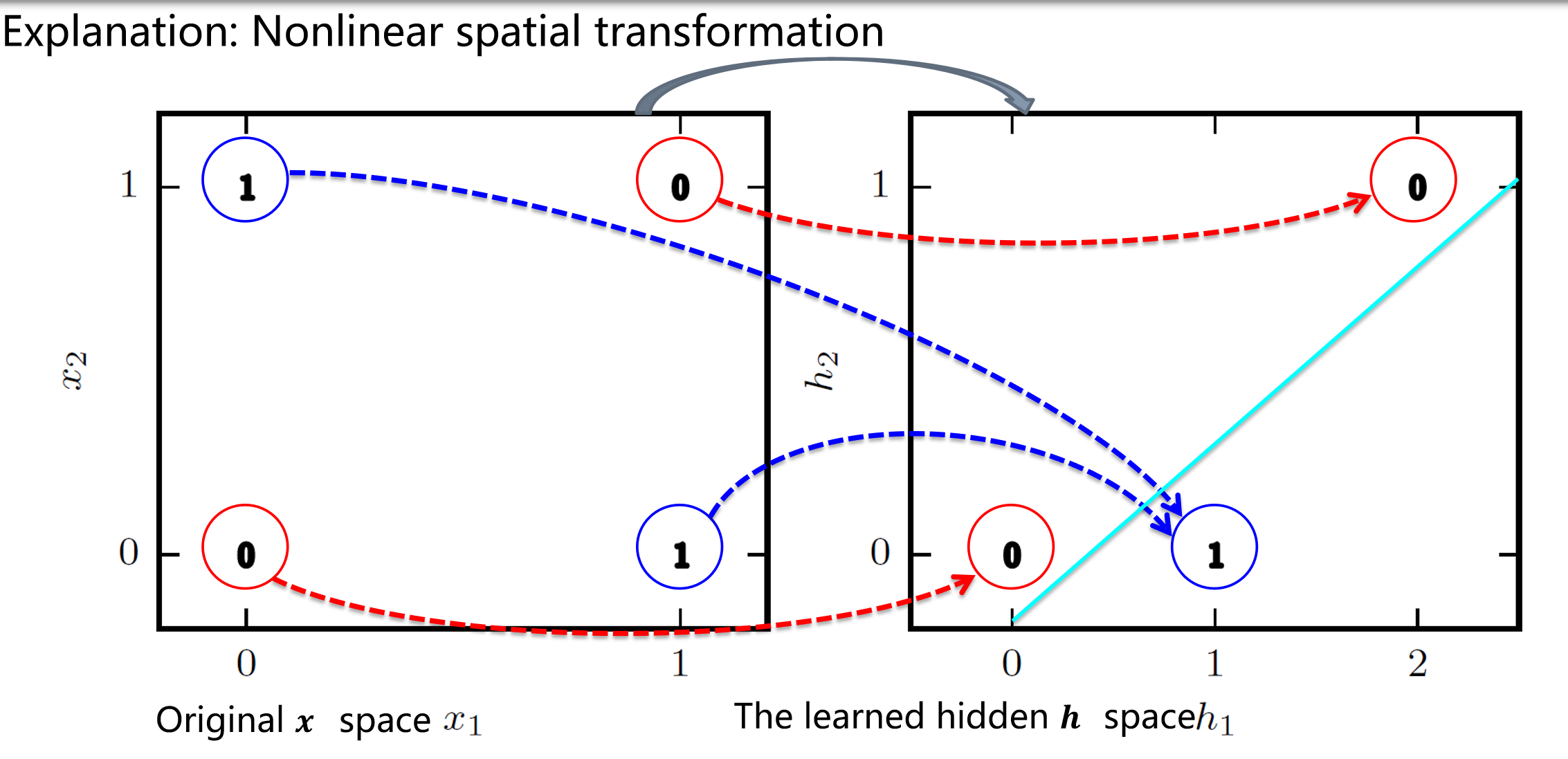
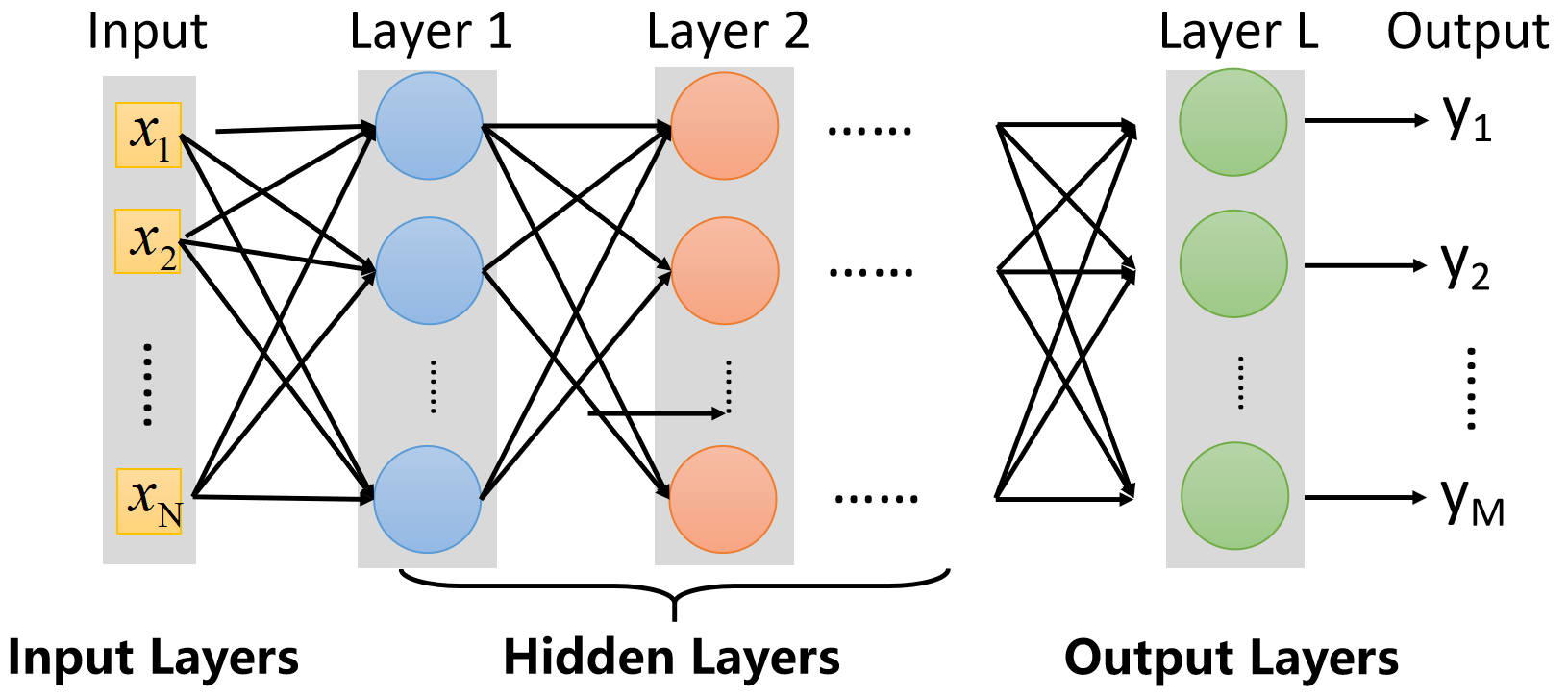
Multi-layer feedforward neural networks

多层前馈神经网络

前馈：输入层接收外部信号，隐层和输出层处理信号，输出层输出处理后的信号

学习：从训练数据中学习，以调整神经元之间的连接权重和功能神经元的阈值。

Error Backpropagation Algorithm

误差反向传播算法（BP）是训练多层前馈神经网络最成功的学习算法。

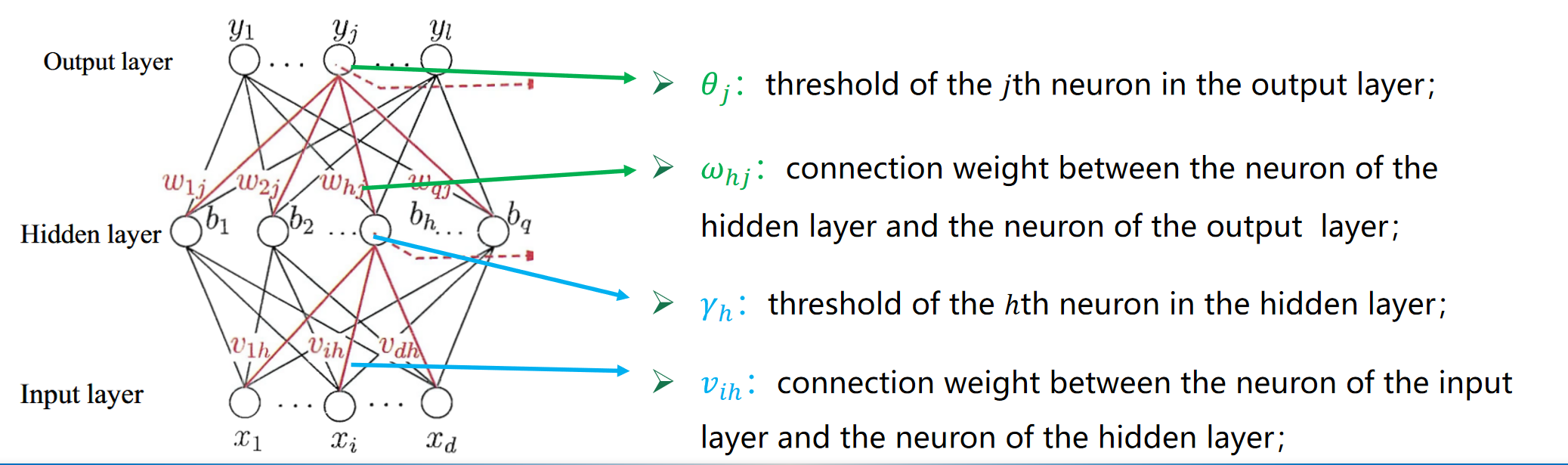
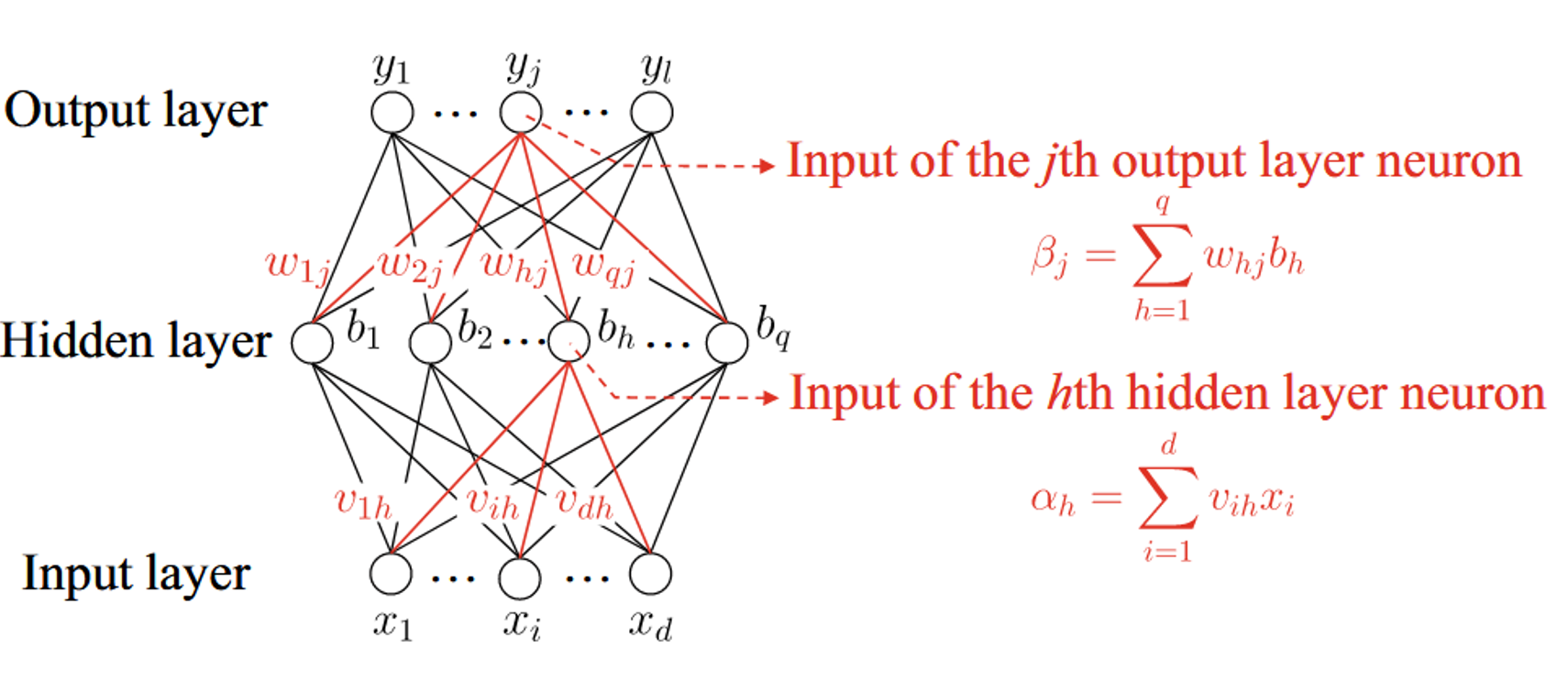
BP 算法则是根据输出值反向传播到输入层，对权重和阈值进一步更新。

怎么更新？更新公式是？

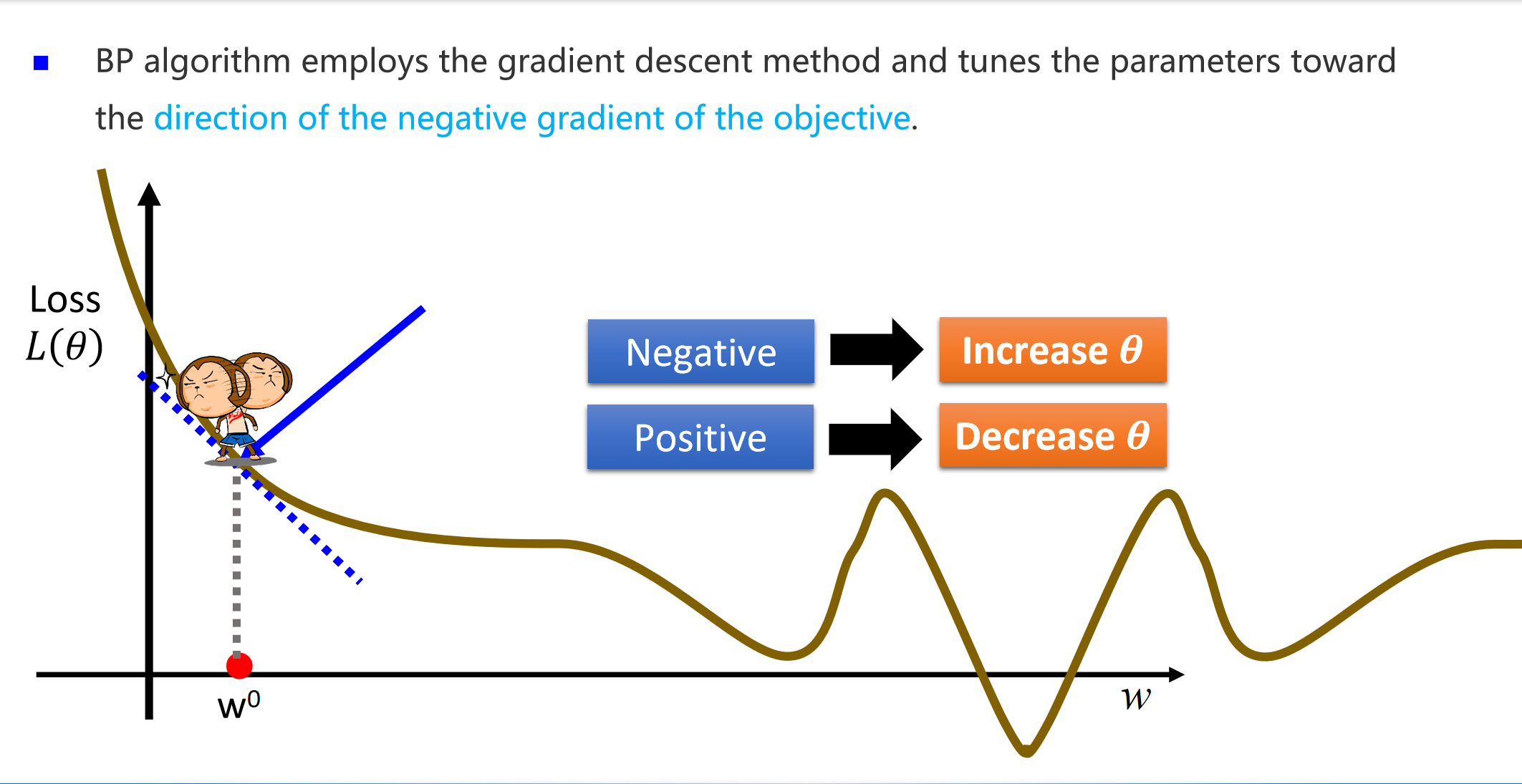
我们同样使用梯度下降大法。递减公式是：

​ $\mathrm{\Delta }{w}_{hj}=-\eta \frac{\partial E_k}{\partial w_{jk}}$

神经网络的目标是通过调整参数（权重 w）来最小化误差函数 $E_k$。

参数更新总结

• 输出层权重更新：

​ $\mathrm{\Delta }{w}_{hj}=\eta g_j{b}_h$

• 隐藏层权重更新：

​ $\mathrm{\Delta }{v}_{ih}=\eta e_h{x}_i$

• 偏置项更新： 输出层：

​ $\mathrm{\Delta }{\theta }_j=-\eta g_j$

​ 隐藏层：

​ $\mathrm{\Delta }{\gamma }_h=-\eta e_h$

其中，$e_h$ 表示隐藏层的误差，具体为：

​ $e_h=b_h(1-b_h)\sum _j{w}_{hj}{g}_j$

$g_j$ 表示输出层误差，具体为：

​ $g_j={\hat{y}}_j^k(1-{\hat{y}}_j^k)(y_j^k-{\hat{y}}_j^k)$

• 步骤：

  输入： 训练集 $(x_k,y_k)$ 和学习率 $\eta$。

  过程：

  • 初始化连接权重和阈值。
  • 重复迭代处理每一个样本：
    1. 计算当前参数下的输出值 ${\hat{y}}_k$。
    2. 计算输出层误差项 $g_j$。
    3. 计算隐藏层误差项 $e_h$。
    4. 更新权重 $w_{hj},v_{ih}$ 和阈值 ${\theta }_j,{\gamma }_h$。
  • 直到满足终止条件。

  输出： 训练好的前馈神经网络。

表示能力

• 多层前馈网络（单隐藏层）具有很强的表示能力，能够逼近任意复杂的连续函数，达到任意精度。

局限性

1. 过拟合问题：
   • 训练误差下降，但测试误差上升，模型过于复杂，泛化能力差。
2. 缺乏原则性方法：
   • 没有确定的方法来设定隐藏层的神经元数量，通常通过“试错法”确定。

Global Minimum and Local Minimum

Strategies to "jump out" from the local minimum

• 使用不同的参数集初始化多个神经网络。取误差最小的那个。

• 模拟退火技术 [Aarts and Korst, 1989]。 以一定的概率接受较差的解，因此可以跳出局部最小值。

• 随机梯度下降法：在梯度计算中引入随机因素，而不是标准梯度下降法中使用的精确计算。

• 遗传算法 [Goldberg, 1989]。常用于训练神经网络，以更好地逼近全局最小值。

Other Common Neural Networks

RBF

特点	RBF网络	一般神经网络 (MLP)
激活函数	局部响应的径向基函数（如高斯函数）	全局响应的非线性函数（如 ReLU、Sigmoid）
结构	单隐藏层，输出层线性组合	多层隐藏层，输出层非线性映射
训练方法	聚类（确定中心） + BP（确定权重）	BP 算法优化所有权重
响应区域	局部响应，适用于插值和分类问题	全局响应，适用于复杂非线性问题
计算复杂度	训练速度快，结构简单	训练复杂，计算量大
应用场景	小样本分类、函数逼近、插值问题	大规模数据，复杂的回归、分类、图像任务

ART

比较维度	ART网络	传统神经网络
学习方式	采用无监督学习，基于竞争学习机制。	主要采用监督学习，如误差反向传播（BP）。
动态性	可以动态添加神经元，适应新数据和新类别。	结构固定，通常在训练前确定神经元数量。
稳定-可塑性	解决稳定-可塑性问题，保留旧知识并学习新知识。	存在灾难性遗忘，学习新数据时可能丢失旧知识。
模式分类	通过识别阈值控制类别粒度（精细或粗略分类）。	无法动态调整类别，分类粒度固定。
增量学习	支持增量学习和在线学习。	需一次性训练整个数据集，不支持增量学习。
网络结构	包含比较层、识别层、重置模块和识别阈值。	通常包括输入层、隐藏层和输出层。
应用场景	适用于自适应模式分类和在线学习任务。	适用于固定分类任务或大规模数据训练。

SOM

类别	内容
全称	Self-Organizing Map（SOM）
提出者	Kohonen（1982）
学习方式	无监督学习
基本原理	- 基于竞争学习的策略。 - 将高维输入数据映射到低维空间（通常是二维），同时保留数据的拓扑结构。
结构	- 输入层：处理输入数据。 - 输出层：神经元排列成矩阵结构（二维空间），每个神经元都有一个权重向量。
工作机制	- 竞争规则：权重向量与输入向量最相似的神经元“获胜”，成为最佳匹配单元（BMU）。 - 邻域更新：获胜神经元及其周围神经元的权重向量向输入数据更新。
训练过程	1. Step 1：到达新样本时，输出层神经元计算权重向量与输入向量的距离，距离最小的神经元获胜。 2. Step 2：更新获胜神经元及其邻域的权重向量。
特点	- 能将高维数据映射到低维空间。 - 保持数据在高维空间中的拓扑结构。 - 神经元以“竞争”的方式进行学习。
应用	- 数据可视化 - 聚类分析 - 特征提取与降维

Cascade Correlation

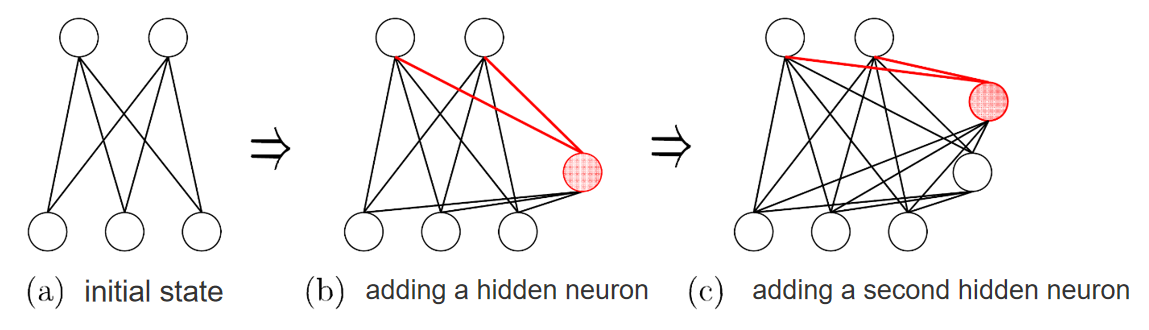
(a) 初始状态 (initial state)

• 网络只有输入层和输出层，没有隐藏层。

(b) 添加第一个隐藏神经元 (adding a hidden neuron)

• 将一个新的隐藏神经元添加到网络中，它与输入层、输出层建立连接。
• 红色线条表示新添加的连接，目的是优化网络性能，减少网络误差。

(c) 添加第二个隐藏神经元 (adding a second hidden neuron)

• 再次添加一个新的隐藏神经元，并将其连接到网络的不同层（包括之前的隐藏神经元）。
• 这种逐步级联的过程，逐渐提升网络的建模能力。

Elman网络

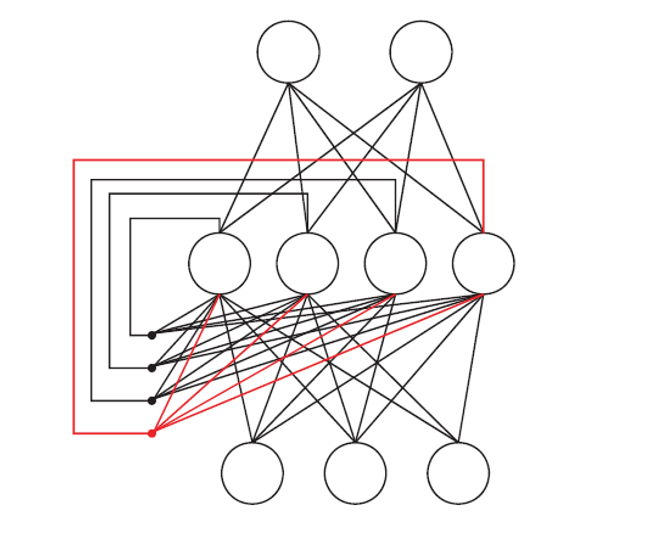
• 结构特点：

  • Elman网络是一种特殊的循环神经网络，其结构与多层前馈网络相似。

  • 区别

    在于：隐藏层的输出会

    反馈

    到网络的下一次迭代中，作为隐藏层的输入之一。

    • 这种反馈连接（图中红色线条）使得网络能够记住之前的状态，具备记忆能力。

  • 输入到隐藏层的信号包含两个部分：

    1. 来自输入层的信号。
    2. 隐藏层输出的反馈信号（上一时间步的隐藏层状态）。

• 工作原理：

  • 在每个时间步，隐藏层的状态不仅依赖于当前输入，还依赖于前一时间步的隐藏层输出。
  • 这种机制使 Elman 网络能够学习时间序列数据中的模式和依赖关系。

**Boltzmann Machine **

1. 能量模型 (Energy-Based Model)：

   • Boltzmann Machine 是一种能量模型，通过最小化网络的能量函数 E(s)E(s)E(s) 来学习数据分布。

   • 网络的目标是通过优化权重 wijw_{ij}wij 和阈值 θi\theta_iθi，使能量函数达到最小值。

   • 能量函数定义为：

     $E(s)=-\sum _{i=1}^{n-1}\sum _{j=i+1}^n{w}_{ij}{s}_i{s}_j-\sum _{i=1}^n{\theta }_i{s}_i$

2. 网络结构：

   • 包含两个主要层次：
     • 可见层 (Visible layer)：输入和输出数据的表示。
     • 隐藏层 (Hidden layer)：学习数据的内在特征表示。
   • Boltzmann Machine 的神经元为布尔型：0 表示未激活，1 表示激活。
   • 在标准 Boltzmann Machine 中，网络是完全连接的，每个神经元都与其他神经元相连。

---

1. Boltzmann 分布：
   • 网络的状态向量 s 的概率服从 Boltzmann 分布：$P(s)=\frac{e^{-E(s)}}{\sum _t{e}^{-E(t)}}$
   • 能量越小，状态的概率越大，网络最终收敛到一个稳定的状态。

---

1. 训练特性：

   • Boltzmann Machine 的训练目标是最大化训练样本的概率，优化网络权重与阈值。
   • 由于全连接的特性，标准 Boltzmann Machine 存在较高的计算复杂度，不适用于实际应用。

2. 受限玻尔兹曼机 (Restricted Boltzmann Machine, RBM)：

   • 为了简化计算，RBM 是一种特殊的 Boltzmann Machine，只保留可见层和隐藏层之间的连接，取消了同层神经元之间的连接。

   • RBM 将网络结构简化为二部图 (Bipartite Graph)，大大降低了计算复杂度。

   • 

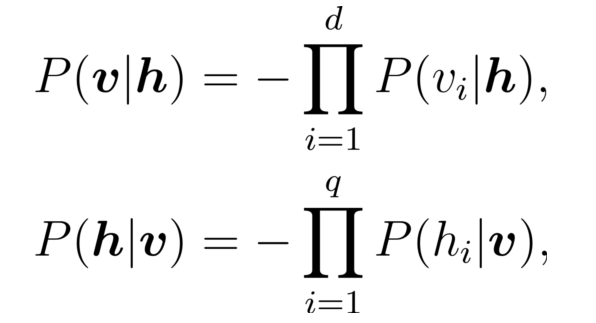
   • RBM 怎么更新权重？

   • For each training sample v, the CD algorithm first computes the probability distribution of hidden neurons and then obtains h by sampling from this distribution. Thereafter, similarly, v′ is generated from h , and h′ is further generated from v′. Then, the connection weight can be updated by:

     

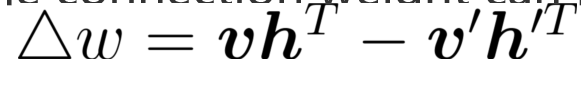
Deep Learning

1. 深度学习模型的特点

• 模型复杂度
  • 增加隐藏神经元（模型宽度）。
  • 增加隐藏层数量（模型深度）。
  • 增加层数的效果更显著，因为更多层不仅引入更多神经元，还增加了激活函数的嵌套，提高了网络的表达能力。
• 复杂模型的难点
  • 多隐藏层网络难以直接用传统算法（如标准反向传播 BP 算法）训练，因为误差容易在多层反向传播过程中发散，无法收敛到稳定状态。

2. 复杂模型训练方法

预训练与微调 (Pre-training + Fine-tuning)

• 预训练 (Pre-training)：
  • 采用无监督逐层训练，即每个隐藏层逐一训练。
  • 先用前一隐藏层的输出作为下一隐藏层的输入，逐层优化参数。
• 微调 (Fine-tuning)：
  • 在预训练基础上，使用反向传播 (BP) 算法对整个网络进行微调，优化整体性能。
• 示例：
  • 深度信念网络 (DBN)：
    • 结构：每一层都是受限玻尔兹曼机（RBM）。
    • 训练方法：无监督预训练 + BP 微调。
• 分析：
  • 通过分组优化参数，逐步优化局部参数，最终联合搜索全局最优解。

权重共享 (Weight Sharing)

• 一组神经元共享相同的连接权重，减少参数数量。
• 应用：卷积神经网络（CNN）。

---

卷积神经网络 (Convolutional Neural Networks, CNN)

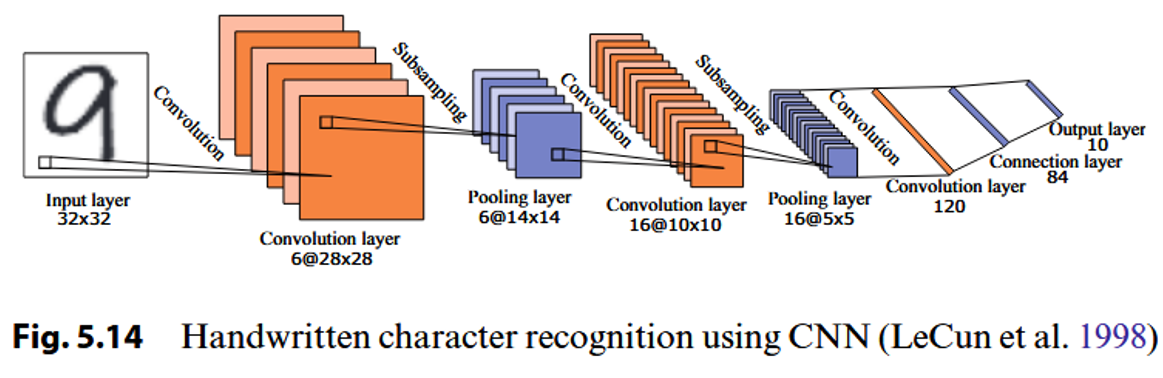
• 结构：

  卷积层（Convolutional Layer）

  • 作用：通过卷积操作提取输入数据的局部特征。
  • 每个卷积层包含多个特征映射（Feature Maps），特征映射是由卷积核（Filter）通过输入矩阵的卷积操作得到的。

  池化层（Pooling Layer）

  • 作用：通过下采样减少数据量，同时保留关键信息。
  • 特点：利用数据的局部相关性进行采样，降低计算复杂度，提高模型的泛化能力。

  连接层（Connection Layer）

  • 作用：将前一层的输出与输出层进行全连接，本质上与传统的全连接神经网络类似。
  • 目标：通过连接层将特征映射到最终的分类或回归任务上。

• 特点：

  • 通过权重共享机制，大幅减少参数量，适用于图像和序列数据处理。

• 示例：

  • 手写字符识别（LeCun et al., 1998）。

激活函数

• 在 CNN 中，Sigmoid 激活函数通常被替换为修正线性单元（ReLU）。
• ReLU 定义为： $f(x)=max(0,x)$
• 优势：ReLU 解决了 Sigmoid 激活函数导致的梯度消失问题，计算更高效。

训练方法

• 反向传播（Backpropagation, BP） 用于训练 CNN。
• 特点：
  • 权重共享：卷积层和池化层中，多个神经元共享相同的连接权重，大幅减少参数量，提高训练效率。
  • 通过共享权重使 CNN 对输入数据的平移不变性（Translation Invariance）更加敏感。

特征工程 vs 特征学习

• 特征工程（Feature Engineering）：
  • 由人类专家手动设计特征，分为特征提取和分类识别两个阶段。

• 特征学习（Feature Learning）：
  • 使用深度学习技术自动生成特征，通过端到端的学习框架实现特征提取与分类识别的一体化。

神经网络模型（FCNN）： 就像对一张图片打碎成碎片，然后将所有碎片混在一起进行处理，最后重新拼凑出结果。但在这个过程中，图片的空间信息丢失了。

卷积神经网络（CNN）： 就像用一个放大镜在图片上逐块观察（卷积核滑动），找到局部特征，然后通过多次观察（多层卷积）逐步理解整个图片的含义。