机器学习第12章

k-Nearest Neighbor Learning

1. 原理

定义：kNN 是一种简单且常用的监督学习算法。

机制：

• 对于一个测试样本，找到其在训练集中最近的 k 个邻居。
• 使用某种距离度量（如欧几里得距离）来判断哪些邻居是最近的。
• 基于这 k 个邻居的类别或特征来预测测试样本的结果。

2. 距离度量:

• 欧几里得距离（Euclidean Distance）：

  • 公式： $d(x,y)=\sqrt{\sum _i(x_i-y_i{)}^2}$
  • 定义：这是最常用的直线距离度量，表示两点之间的实际空间距离。
  • 场景：在 2D 和 3D 空间中最为直观，适用于计算点之间的直接距离。

• 曼哈顿距离（Manhattan Distance）：

  
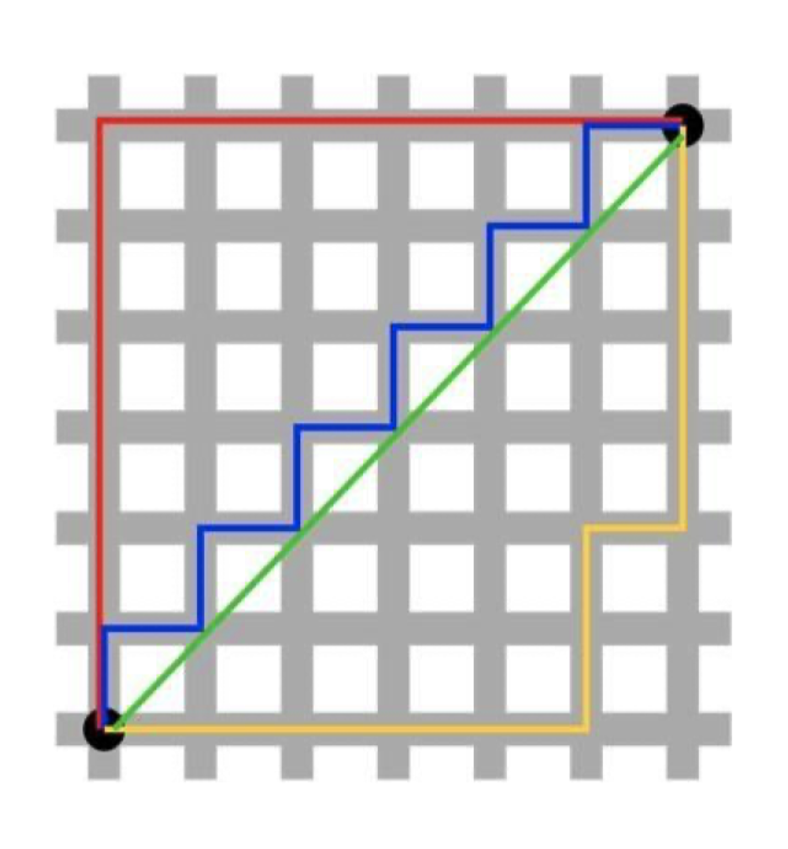
  • 公式：$d(x,y)=\sum _i|x_i-y_i|$
  • 定义：图中展示的红色和蓝色路径是曼哈顿距离（Manhattan Distance），也被称为城市街区距离（City Block Distance）。这类距离度量方法是计算从一个点到另一个点在直角网格上的水平和垂直移动距离之和。。
  • 别名：又称为城市街区距离（City Block Distance）。
  • 场景：适用于网格或正交路径的场景，比如城市道路导航。

• 切比雪夫距离 (Chebyshev Distance)：

  • 公式：最大坐标差值：$d(x,y)=\underset{i}{max}(|x_i-y_i|)$
  • 解释：类似棋盘上国王移动的最少步数。
  

• 闵可夫斯基距离 (Minkowski Distance)：

  • 公式：$d(x,y)={(\sum _i|x_i-y_i{|}^p)}^{\frac{1}{p}}$

  • 特殊情况：

    • $p=1$：曼哈顿距离。
    • $p=2$：欧氏距离。
    • $p=\mathrm{\infty }$：切比雪夫距离。

3. 选取特征

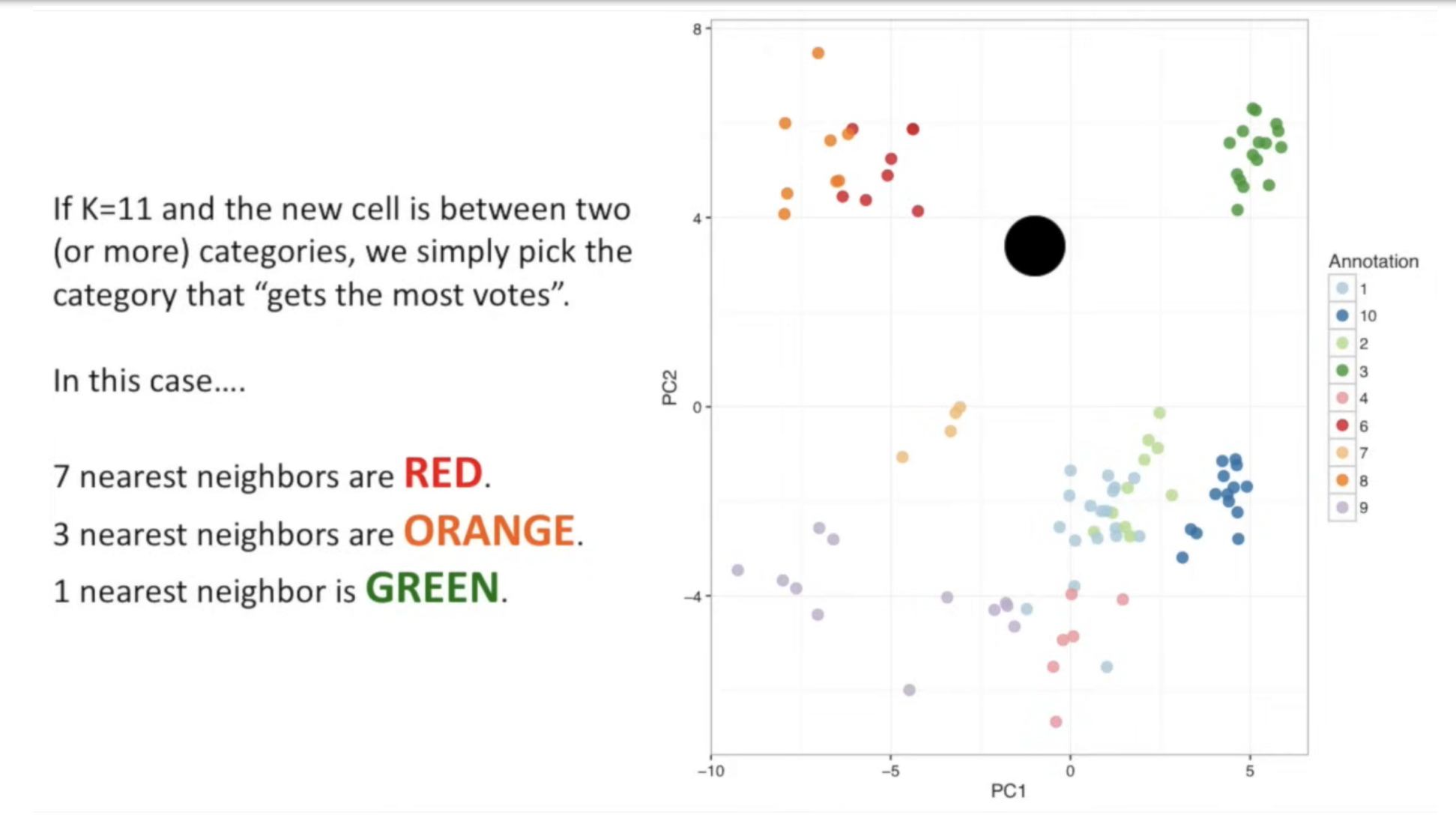
投票法：在这𝒌 个样本中选择最常见的类别标签作为预测结果。(分类任务） 平均法： 取这 𝒌 个样本的实值输出标签的平均值作为预测结果。(回归任务）

此外，还可以根据距离进行加权平均或加权投票，距离越近，样本的权重越大。

流程：

1. 计算距离：对测试样本与训练集每个样本计算距离；
2. 排序：按距离升序排列；
3. 选取邻居：选择距离最近的k个训练样本；
4. 投票或平均：根据分类或回归任务计算预测结果。

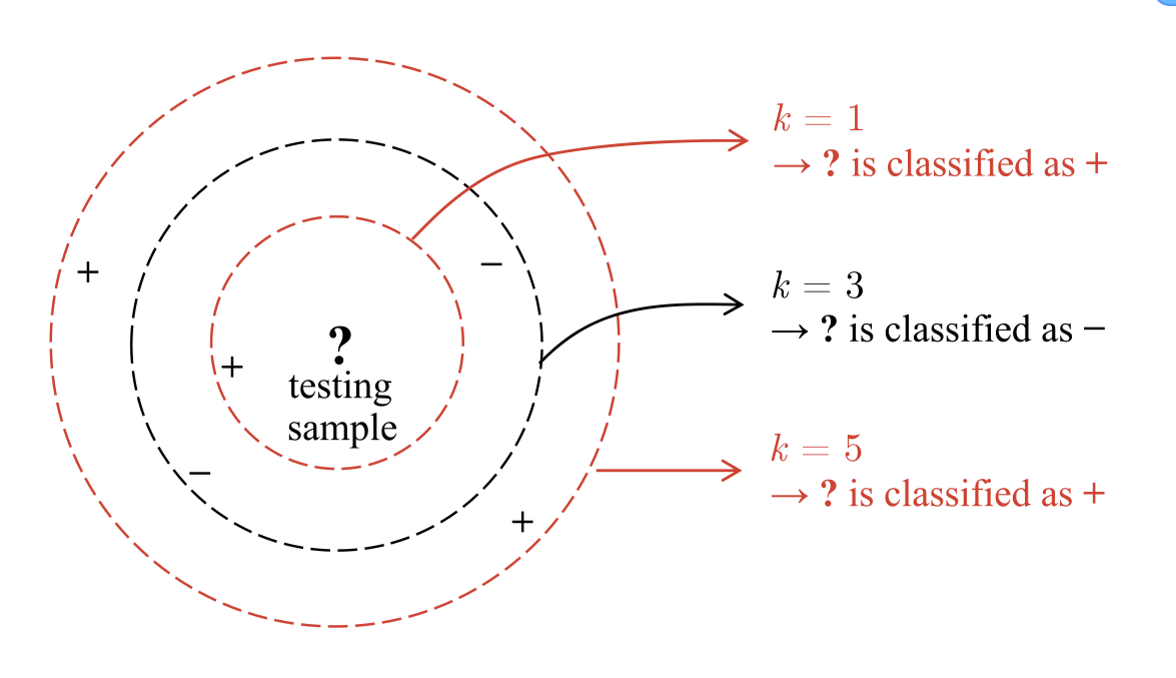
我们可以看到，参数 k 起着重要作用，因为不同的 k 值可能会导致截然不同的分类结果。此外，不同的距离计算也会导致明显不同的 “邻域”，从而导致不同的分类结果。

4. 误分类率

5. 步骤

步骤 1：从已知类别的数据集开始

• 数据集：包含不同细胞类型（如肠道肿瘤中的细胞）的标注数据。
• 方法：利用 主成分分析 (PCA) 对数据进行降维并可视化。
  • PCA 的作用：将高维数据投影到低维空间（例如二维），以便观察数据分布和聚类特征。
• 图示：每种颜色的点代表不同类别的细胞，PCA 的两个主成分（PC1 和 PC2）用于表示数据分布。

步骤 2：添加未知类别的样本

• 描述：在 PCA 图中加入一个未知类别的细胞。
  • 这个新细胞的数据来源于另一肿瘤，没有明确的类别信息。
• 目标：通过现有的标注数据推断新细胞的类别。
• 关键点：新细胞位置靠近哪些类别的标注样本是分类的依据。

步骤 3：利用最近邻方法进行分类

• 方法：通过观察新细胞的最近邻样本的类别来决定它的类别。

  • 最近邻分类：找到 PCA 图中最接近未知样本的标注数据点。
  • 假设：相似的样本更可能属于同一类别。
  

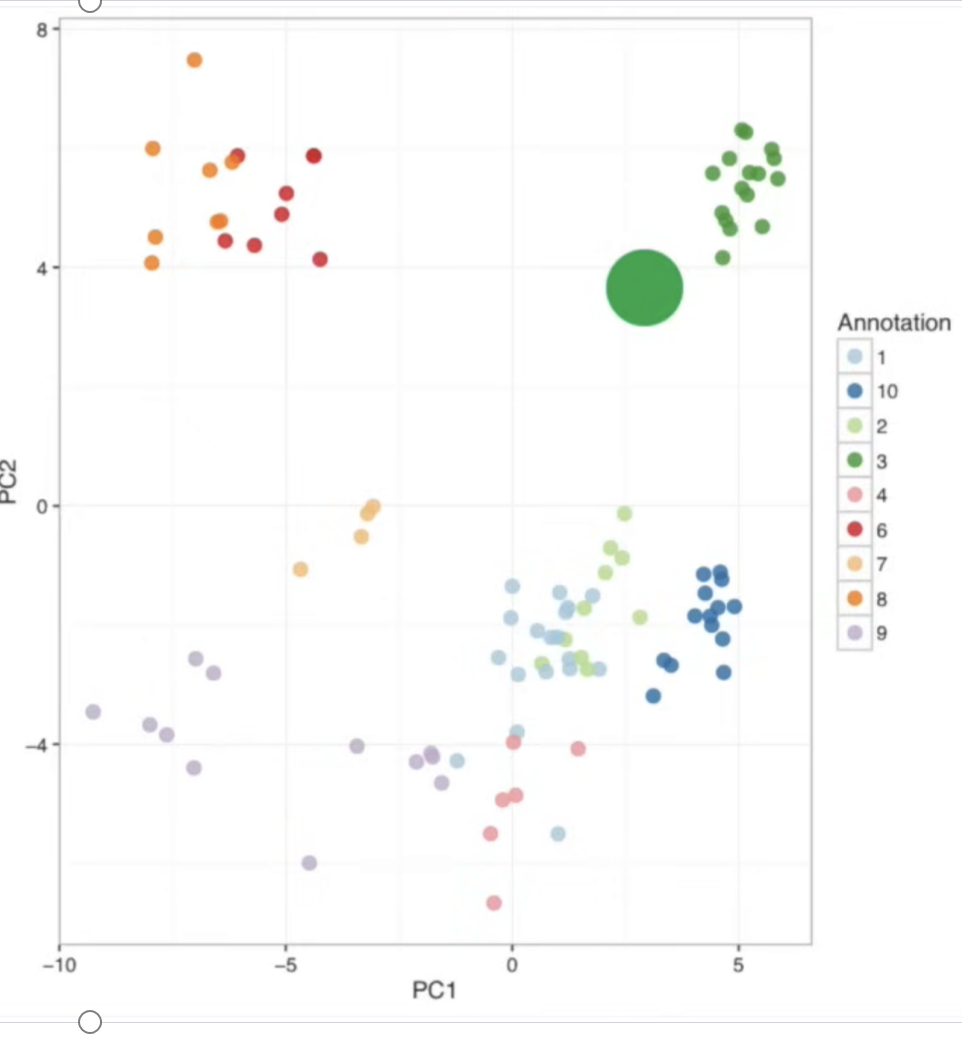
绿色的大坨坨是新细胞，它被划分到了绿色一类，因为离其最近。

• 黑坨坨：
  • 

所以它是红色一类。

6. 如何选择 K 值的关键点总结

• 平衡选择：过小的 K 容易过拟合；过大的 K 容易欠拟合。
• 验证集调整：通过交叉验证测试不同 K 的分类性能，选择最优值。

Low-Dimensional Embedding

1. 维度灾难 (Curse of Dimensionality)

• 定义：在涉及向量计算的问题中，随着维度的增加，计算复杂度以指数级增长。
• 问题描述：
  • 数据维度越高，样本间的距离差异变得不显著，导致算法的性能下降。
  • 高维空间中数据变得稀疏，样本密度降低，影响模型泛化能力。

应对方法：降维 (Dimension Reduction)

• 核心思想：

  • 通过数学变换将高维属性空间转化为低维“子空间”。
  • 降维后样本密度提高，距离计算更容易。

• 常见方法：

  • 主成分分析 (PCA)：寻找数据的主要变化方向，降低冗余维度。

  • 线性判别分析 (LDA)：寻找能够最大化类别分离的低维空间。

    

• 优缺点：

  优点：

  1. 降低特征维度可减少存储空间及训练时间。
  2. 提高数据可视化效率。
  3. 消除冗余特征。

  缺点：

  1. 降维可能导致部分数据丢失。
  2. 确定降维后的维数（如 PCA 的主成分数量）具有一定挑战性，需经验判断。

2. MDS

例子

Principal Component Analysis 主成分分析

1. 当变量超过三个时，它们之间的关系变得更难以可视化。

2. 主成分分析（PCA）

   生成了一组新的变量：

   • 每个主成分是原始变量的线性组合。
   • 所有主成分彼此正交，因此没有冗余信息。
   • 主成分整体形成了数据空间的一个正交基。

3. PCA 是一种降维方法：它通过将原始数据的高维特征集转换为更小的特征集来减少原始数据的维度，同时保留大部分原始数据的信息。

4. 减少数据集中的特征数量通常会牺牲一些精度，但降维的关键在于用一定的精度损失换取简化：

   • 更小的数据集更容易探索和可视化。
   • 对机器学习算法来说，处理较少的特征可以更快更简单。

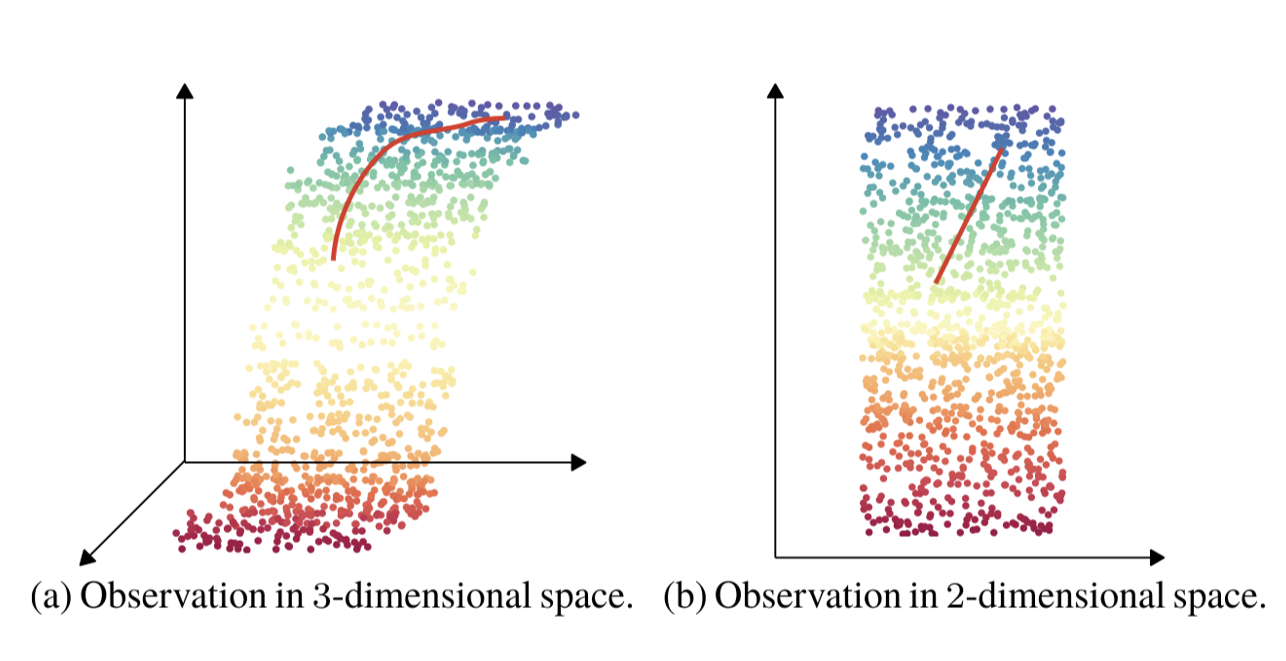
图片的含义

如何降维？

1. 前置知识

如何使用超平面（即二维空间中的一条线，概括为高维空间）来表示样本？

• 最小重构误差：样本应该与该超平面的距离尽可能短；
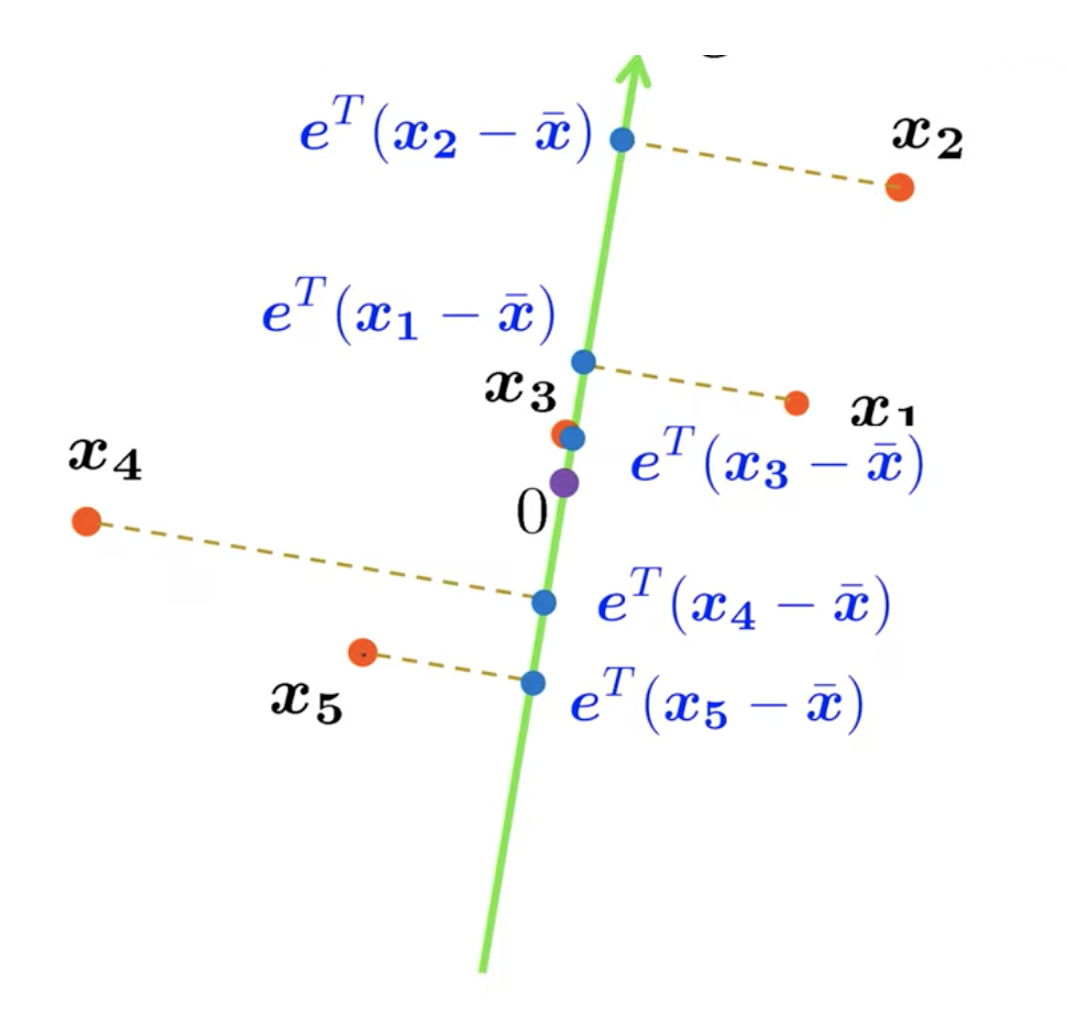
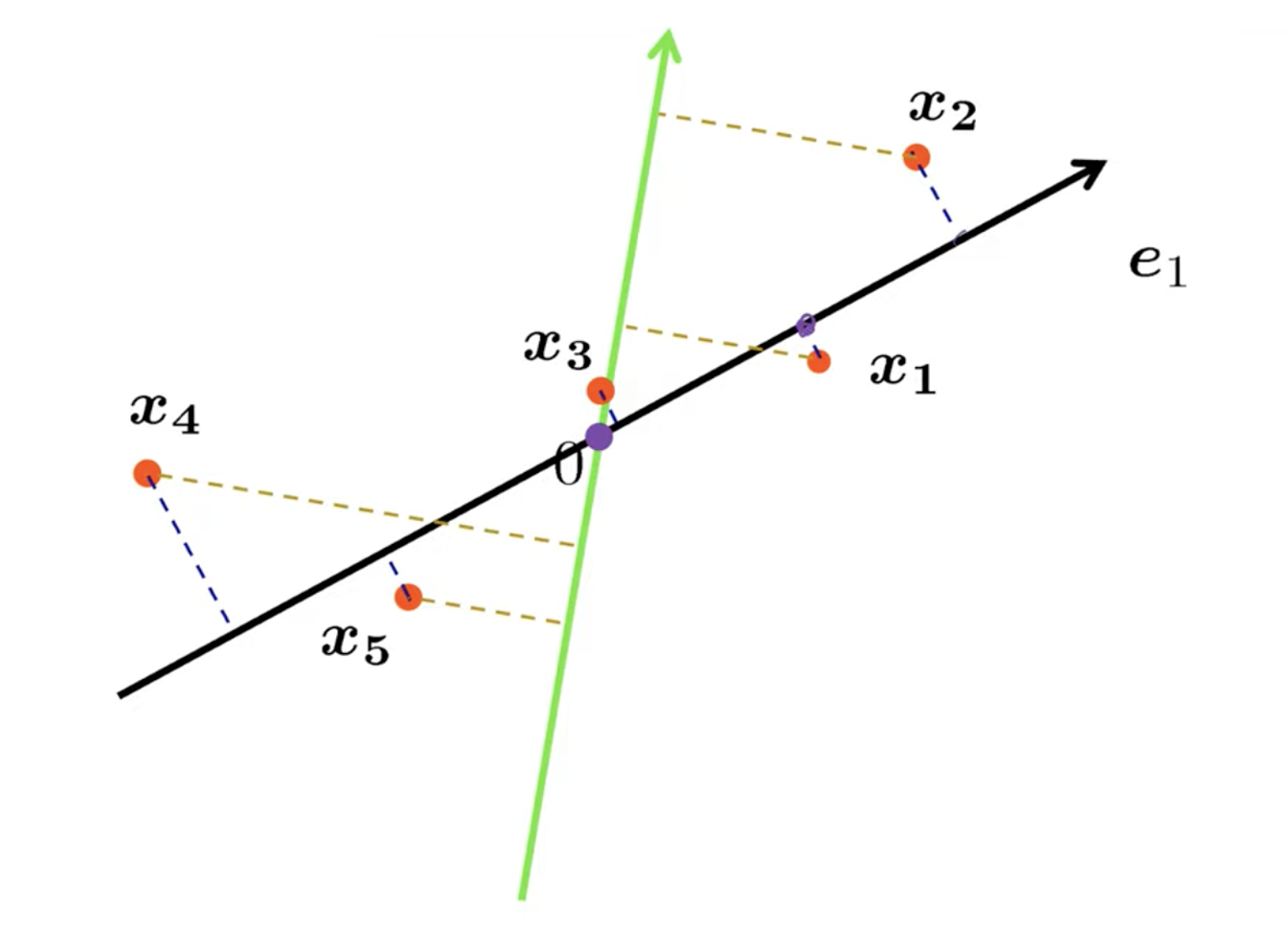
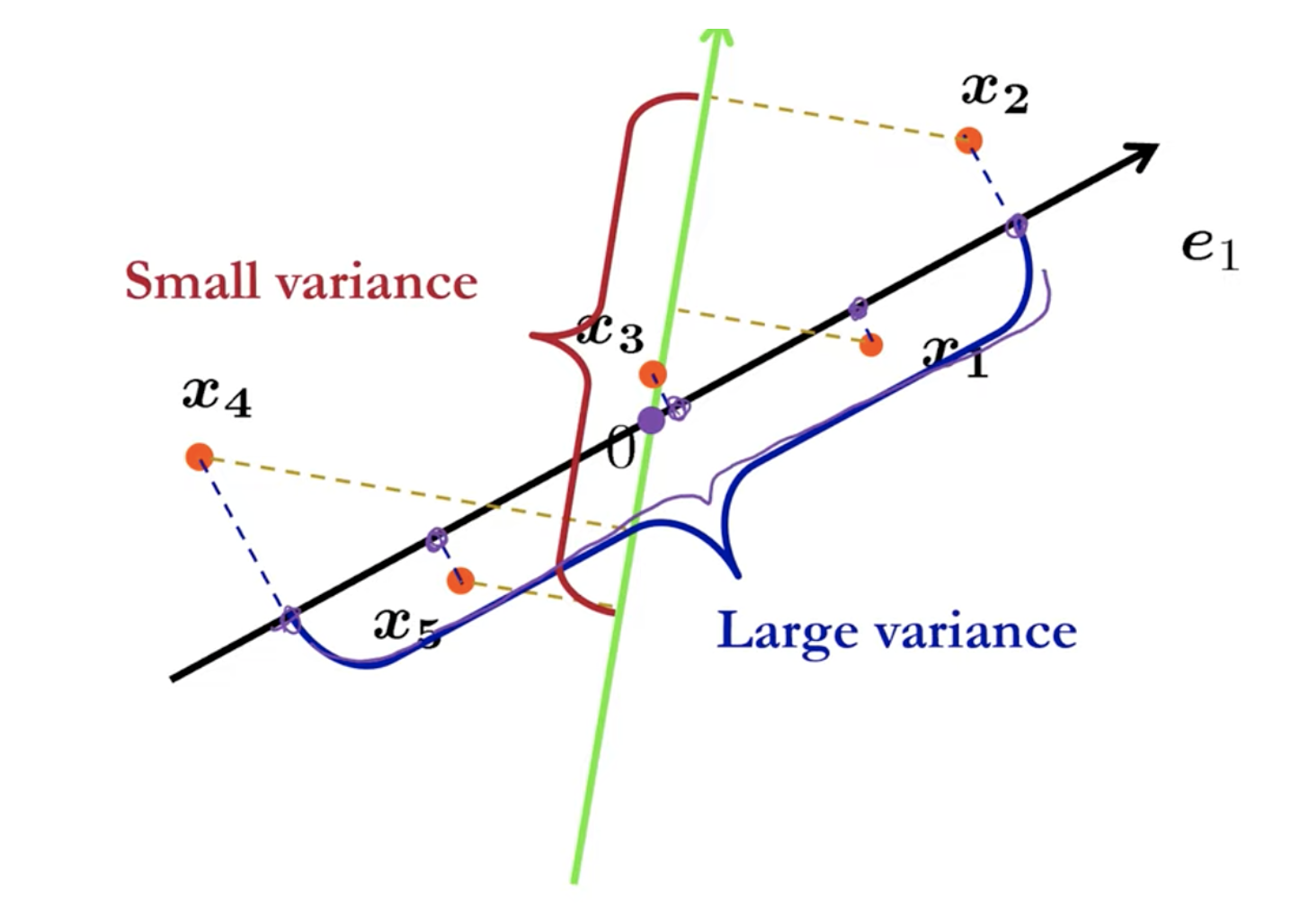
• 最大方差：样本投影到超平面上的点应该尽可能彼此远离。

有趣的是，上述两个性质导致了PCA的两种等价推导。首先，让我们通过最小化重构误差来推导PCA。

• 最终公式： 协方差矩阵的特征分解：

​ $\mathbf{X}{\mathbf{X}}^{\mathrm{\top }}{\mathbf{w}}_i={\lambda }_i{\mathbf{w}}_i$

其中 ${\lambda }_i$ 是特征值，${\mathbf{w}}_i$ 是对应的特征向量。

数学结论

2. 算法步骤

输入：

• 数据集 $D=\{x_1,x_2,\dots ,x_m\}$
• 降维目标维度 $d\prime$

过程：

1. 数据中心化：计算数据均值 $\overline{x}$，并将每个样本点减去均值。
2. 计算协方差矩阵 $\mathrm{\Sigma }=\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T$。
3. 对协方差矩阵进行特征值分解，得到特征值和特征向量。
4. 选择前 $d\prime$ 个最大特征值对应的特征向量 $w_1,w_2,\dots ,w_{d^{\prime }}$ 组成投影矩阵 $W^{\ast }$。

输出： 投影矩阵 $W^{\ast }$，用于将数据从高维投影到低维空间

3. 举例 2D-1D 降维

VS MDS

特性	PCA	MDS
核心侧重点	保留数据的方差信息（主成分）	保留点对之间的距离关系
输入数据类型	样本特征矩阵 X	距离矩阵或样本间的相似度
假设	数据是线性的，使用欧几里得距离	可以处理非线性关系，支持非欧几里得距离
输出解释	主成分是原始特征的线性组合，可解释为特征权重	输出的低维坐标是点间关系的表示，缺乏明确的特征含义
主要用途	降维、特征提取、数据压缩	可视化、非线性数据的关系保持
复杂性	相对简单	经典 MDS 较简单，非线性 MDS 计算复杂

Kernelized PCA

线性降维方法假设从高维空间到低维空间的函数映射是线性的。然而，在许多实际任务中，可能需要非线性映射来找到合适的低维嵌入：

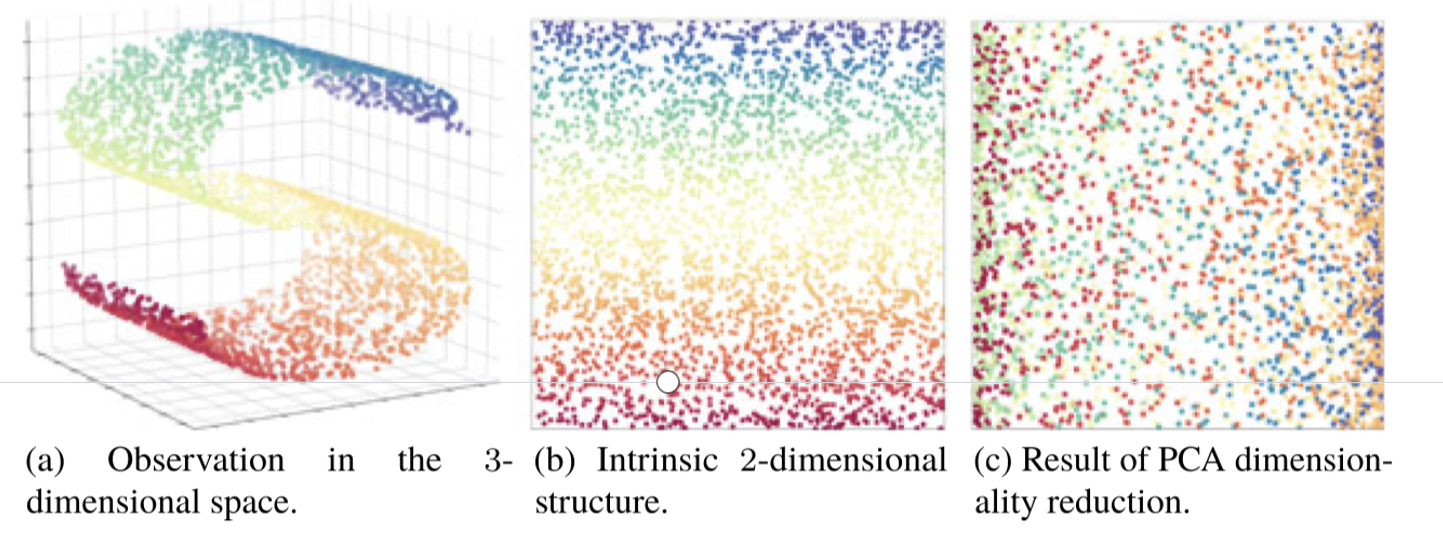
1. 想象一个复杂的二维平面： 比如一个二维的“月牙形”数据集，在原始二维平面中，数据看起来很复杂，没法用一条直线将它们分开或理解。
2. 核函数的魔术： 核函数并不是直接在原始平面里工作，而是“偷偷”将这个数据映射到一个更高维的空间。例如，它可能把二维的“月牙形”拉伸成三维空间中的一个“球形”。
3. 在高维空间做简单的事： 在这个三维空间里，原本复杂的“月牙形”现在变成了“简单的球形”，这时我们可以轻松找到一条直线（或者一个平面）来分开数据点，或者提取主成分。
4. 神奇之处：只用核函数计算： 核函数不需要我们显式地知道高维空间是什么样子，它直接在原始空间中，通过计算数据点之间的“相似性”（用核函数表示，比如高斯核、线性核等），就能完成高维空间的处理。

例子：

• 假设你有两个数据点 $x_1=(1,2)$ 和 $x_2=(3,4)$，它们在二维平面上看起来关系很复杂。
• 核函数（比如高斯核）可以隐式地把它们映射到高维空间，而在这个高维空间中，它们可能看起来是两个更容易区分或分析的点。
• 我们不用明确知道它们高维的具体坐标，而是通过核函数直接比较点与点的关系。

Manifold Learning

• 流形学习就像在地图上表示地球。虽然地球表面很复杂，但地图通过局部平面化来呈现地球的核心信息。

• 欧几里得距离相当于“开直升机飞越大洋”，地质距离则相当于“沿着道路步行到达目的地”，更符合现实。

1. Isometric Mapping

传统的降维方法（如 PCA）是基于线性假设的，即数据可以通过线性变换映射到低维空间。然而，对于复杂的非线性结构数据，这些方法往往无法保留数据的内在几何结构。

Isomap 则通过考虑数据的非线性结构，基于流形假设（数据分布在一个非线性低维流形上）设计出保留全局几何关系的降维方法。

2. Locally Linear Embedding

局部线性嵌入试图保持邻域内的线性关系，并使其在降维空间中继续保持。

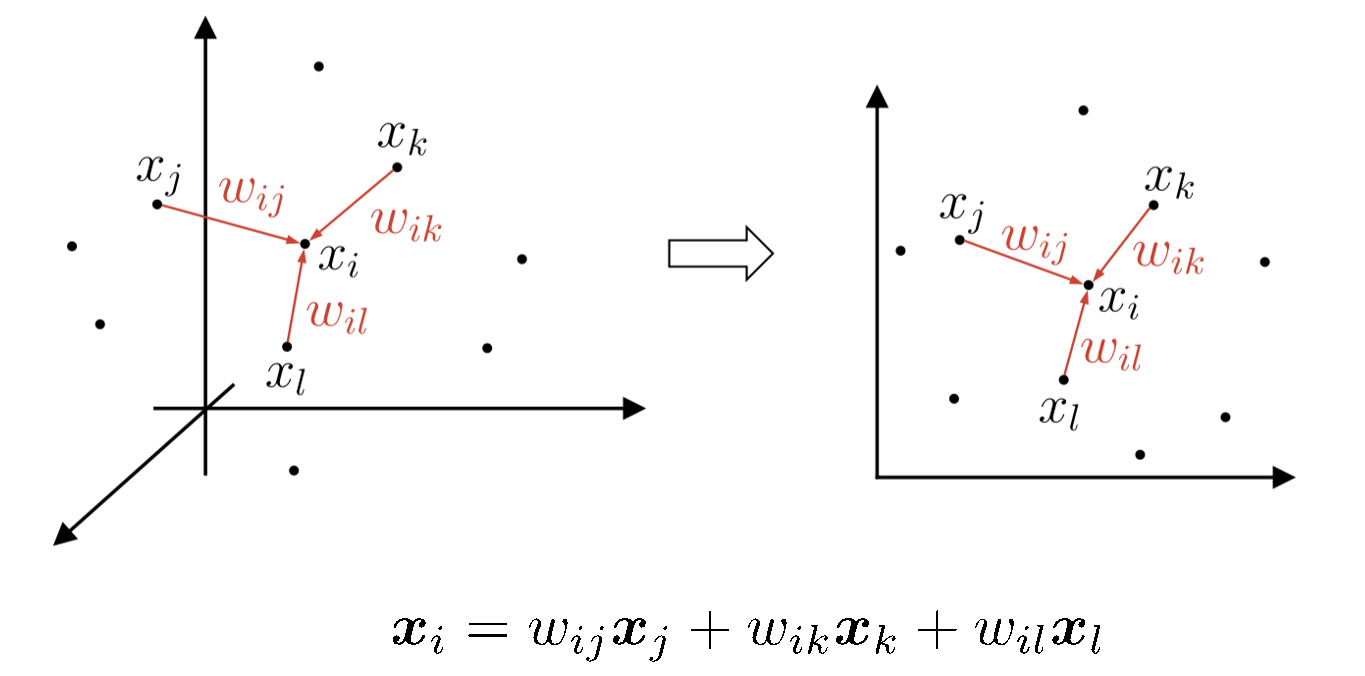
LLE 的关键在于它利用了数据的 局部线性结构，而忽略了全局流形结构的建模。这使得 LLE 在某些非线性问题中表现出色，尤其是当数据局部线性假设较强时。例如：

• 图像中的姿态变化（局部特征通常呈现线性关系）。
• 社交网络中相似用户的行为模式。

与其他方法的对比：

1. 与 Isomap 的对比：
   • Isomap 是一种基于全局测地距离的流形学习方法，它尝试找到数据点之间的全局流形结构，保留的是测地距离。
   • LLE 则专注于局部线性关系，忽略全局测地结构。
   • 总体来说，Isomap 更适合流形结构较为平滑的数据，而 LLE 更适合局部线性假设成立的数据。
2. 与 PCA 的对比：
   • PCA 假设数据是全局线性分布的，目标是找到高维空间中能够解释最大方差的线性投影。
   • LLE 不要求全局线性，能处理更复杂的非线性分布。
3. 与 Kernel PCA 的对比：
   • Kernel PCA 使用核函数将非线性数据映射到高维空间，再在该高维空间中寻找主成分。
   • LLE 直接在原始空间中通过邻域构建局部线性模型。

Metric Learning

通俗解释这个算法的机理和作用：

这个算法是 度量学习——Metric Learning 的一种方法，目标是学习一个优化的距离度量（通过矩阵 M 或 P），使得在这种度量下，数据点的距离更能反映其类别或标签的分布。这种优化的度量可以提升分类器（尤其是最近邻分类器）的性能。

1. 基本机理：
   • 通常使用欧几里得距离来衡量数据点之间的相似性，但这种距离未必能很好地反映数据的特性（例如某些维度更重要）。
   • 通过度量学习，定义了一个可学习的距离矩阵 M，它可以为不同维度分配不同的权重或进行维度变换，捕捉特定的结构。
   • 优化目标是让相似的点在新的度量下更接近，不相似的点更远离。
2. 公式分析：
   • 距离定义：${\text{dist}}_{\text{mah}}(x_i,x_j)=(x_i-x_j{)}^{\mathrm{\top }}M(x_i-x_j)$ 通过矩阵 M 将欧几里得距离推广。
   • 目标函数：最大化最近邻分类器的性能。具体来说：
     • 定义 $p_{ij}$ 表示点 $x_i$ 与其邻近点 $x_j$ 的相似性概率，优化 M 使 $p_{ij}$ 正确分类的概率最大。
3. 优化过程：
   • 优化问题最终转换为一个矩阵 $M=P^{\mathrm{\top }}P$，同时优化矩阵 P。
   • 算法通过优化 P 来调整原始数据空间，学习出一个投影矩阵或变换。

和其他功能一致的算法的区别：

1. 与 PCA 的区别：
   • PCA 是线性降维方法，通过最大化方差找到主成分，而度量学习关注距离定义，通过调整度量优化分类性能。
   • PCA 的降维目标和分类无关，而度量学习直接与分类目标相关联。
2. 与 LLE 的区别：
   • LLE 保留局部线性关系，用于非线性降维，但不直接针对分类任务。
   • 度量学习强调学习一个度量空间，优化分类准确性，与降维不是直接目标。
3. 核心特点：
   • 度量学习直接结合分类任务，学习出的距离度量在分类或聚类中更有效。
   • 可嵌入到最近邻分类器中，提升其性能。

总之，度量学习的核心是：通过学习优化的距离定义，使数据在新的度量空间中更利于分类或聚类。