机器学习第11章

XiaoXianYue原创2024年12月26日大约 10 分钟

Clustering Problem

它是 “无监督学习 ”任务中研究最多、应用最广泛的一种方法。
聚类目标：将数据集中的样本分成几个通常互不相交的子集（簇）。
聚类可以作为一个单独的过程（发现数据的内在分布结构），也可以作为分类等其他学习任务的前奏。

应用场景：

用户画像：根据行为或特征对用户进行分组，以提供个性化服务。
新闻聚类：将相似的新闻归为一类，便于内容管理或推荐。
基因分析：根据基因数据寻找潜在模式或结构，推动生物医学研究。

Performance Measure

聚类性能的直觉：好的聚类应该做到“类内相似度高，类间相似度低”，即：

同一聚类中的样本应该尽可能相似。
不同聚类中的样本应该尽可能不同。

聚类性能指标（Validity Index）：

外部指标（External Index）：将聚类结果与参考模型（例如预先给定的分类标签）进行比较。
内部指标（Internal Index）：直接评估聚类结果的质量，而不需要参考模型。

样本对的分类：

样本对可以按照是否属于同一类以及参考模型的结果，分为以下四类：
- SS：同一聚类且参考模型也认为它们是同一类。
- SD：同一聚类但参考模型认为它们不是同一类。
- DS：不同聚类但参考模型认为它们是同一类。
- DD：不同聚类且参考模型认为它们不是同一类。

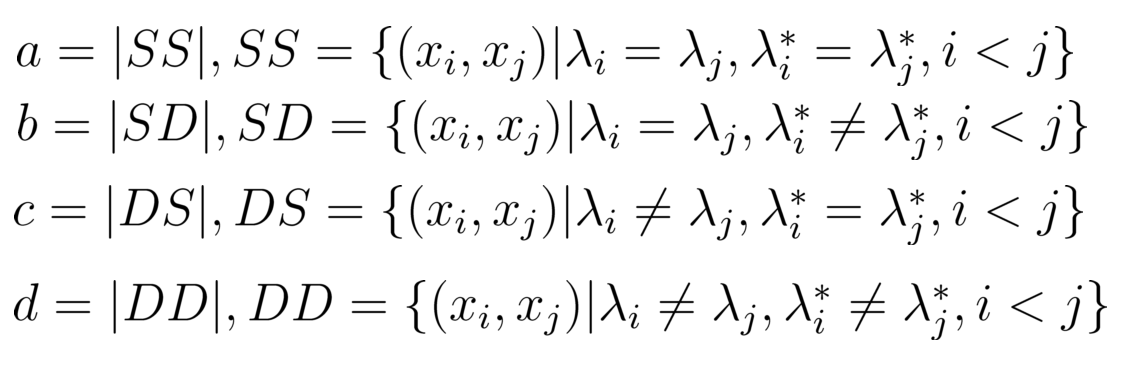
内外部衡量

*Distance calculation

距离度量的性质：

非负性：距离不可能是负数。
身份性：两个点相同时，距离为零。
对称性：点A到点B的距离等于点B到点A的距离。
三角不等式：从点A到点C的距离不超过通过点B的距离和。

属性分类与距离计算：

连续型属性：属性值可以取无限多种可能，例如温度、身高。
离散型属性：属性值有限，可以进一步分为：
- 有序属性：值之间有顺序，例如1, 2, 3。
- 无序属性：值没有顺序，例如飞机、火车、轮船。

三个公式

Distance Metrics

通俗举例：

VDM 示例：
- 属性 u：颜色，取值 {红，绿，蓝}。
- 类别分布：红 (80% 属于 A 类，20% 属于 B 类)；绿 (30% 属于 A 类，70% 属于 B 类)。
- 通过计算分布差异来衡量「红」和「绿」之间的距离。
MinkovDM 示例：
- 数据集包含连续属性「身高」和离散属性「城市」。
- 使用 Minkowski 距离计算身高差异，使用 VDM 衡量不同城市间的类别分布差异，然后综合计算总距离。
加权距离示例：
- 属性包括「收入」和「年龄」，收入更重要，权重为 0.7，年龄权重为 0.3。
- 根据权重调整距离贡献。

Prototype Clustering （原型聚类）

定义：基于原型的聚类算法，假设聚类结构可以通过一组原型（如均值向量）描述。
流程：
1. 初始化原型（簇中心）。
2. 根据样本分配最近的原型。
3. 更新原型为对应簇中样本的均值。
4. 重复以上步骤直到收敛。
目标函数：最小化平方误差：

$E = \sum_{i = 1}^{k} \sum_{x \in C_{i}} ∥ x - μ_{i} ∥^{2}$

代表算法：
- K-means
- 学习向量量化（LVQ）
- 高斯混合聚类（GMM）

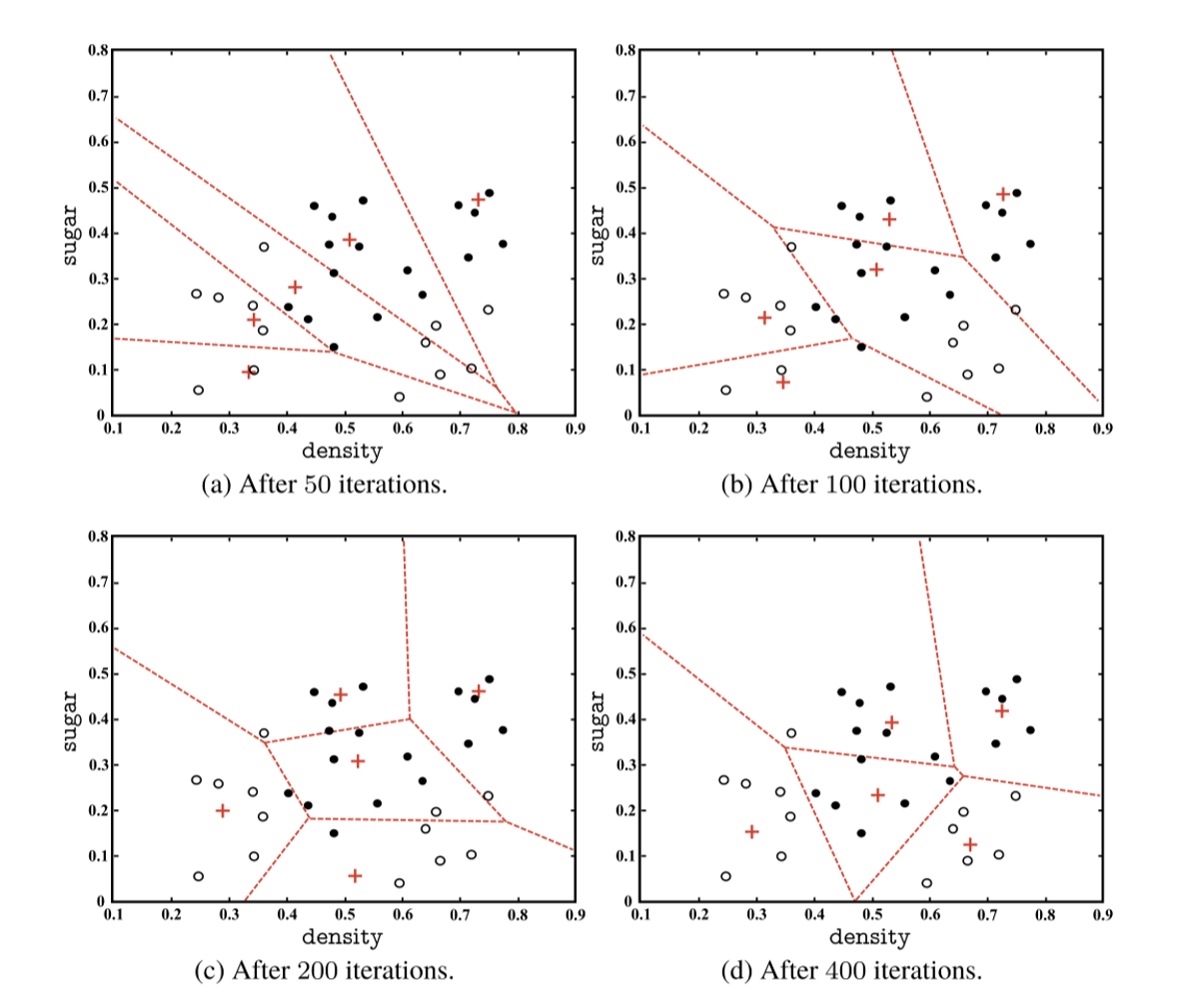
K-means —— 原型聚类

1. 介绍

2. 例子

3. 不同训练集

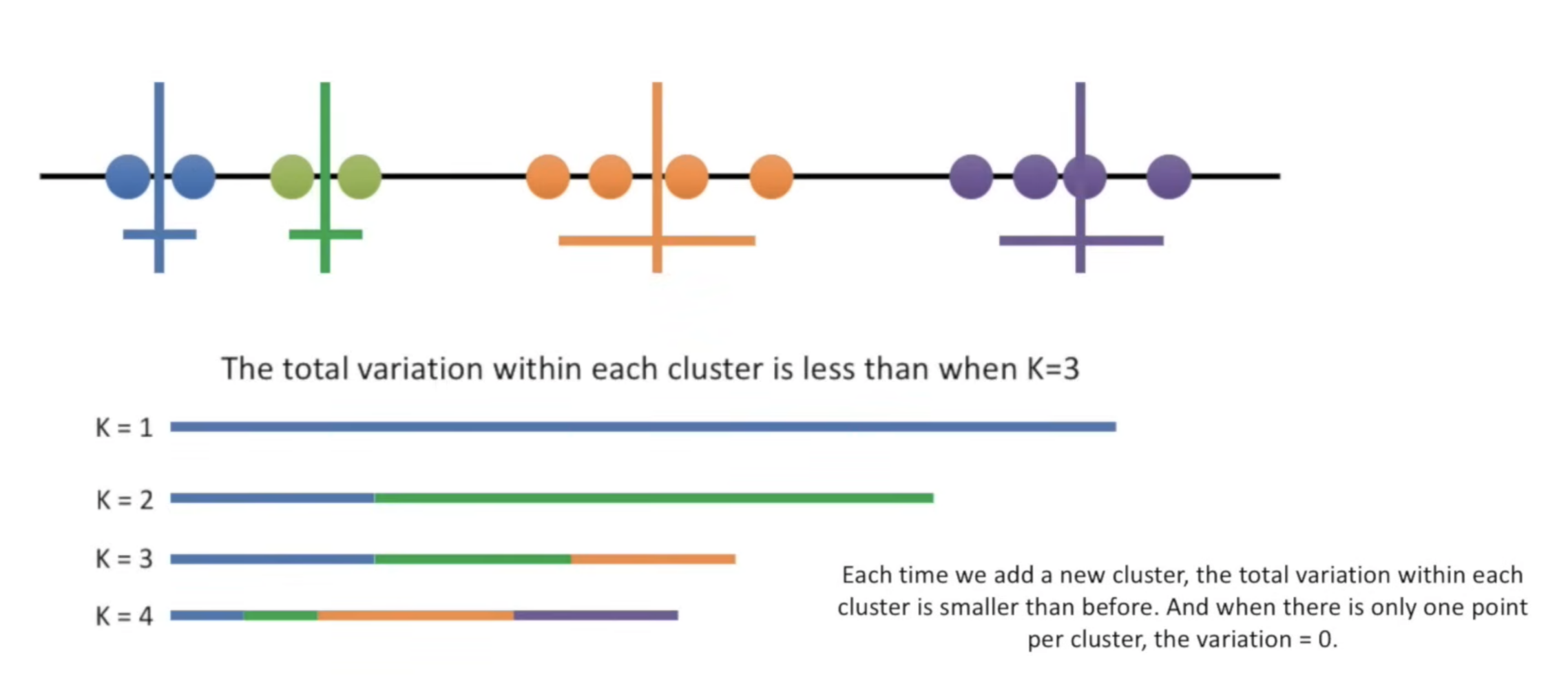
每当我们增加一个新的簇时，每个簇内的总变异都会比之前更小。当每个簇只有一个点时，变异值为 0。

初始时选择不同的点当做簇的中心，最后训练出来的分类结果也不一样。

4. 图示和例子

K值选择和肘部法则：

数据划分成多个簇，每个簇的内部差异随着增加的簇数逐渐减少。
绘制减少的差异与簇数的关系图，可以通过"肘部"点来选择最佳簇数K。
示例图中，当K=3时，差异减少显著，但继续增加簇数差异减少的幅度减小。

Learning Vector Quantization —— 原型聚类

区别于普通聚类算法：LVQ属于监督学习算法，假设数据样本带有类别标签，并利用这些标签信息辅助聚类过程。

目标：给定样本集 $D = {(x_{1}, y_{1}), (x_{2}, y_{2}), \dots, (x_{m}, y_{m})}$ ，（y 是标签）学习出一组 n-维原型向量 $p_{1}, p_{2}, \dots, p_{q}$ ，每个向量表示一个类别的中心。

过程：

初始化原型向量；
根据样本和原型向量之间的距离进行分类；
更新原型向量，使其更靠近正确分类样本，远离错误分类样本。

VS K-means

标签干啥使的

软硬聚类

Hard Clustering（硬聚类）

定义：每个数据点被明确分配到一个唯一的簇中。
特点：
- 数据点与某个簇的关系是“属于”或“不属于”。
- 没有模糊性。
算法示例：
- K-Means
- Hierarchical Clustering
应用：适用于明确分类的数据，比如用户群划分。

Soft Clustering（软聚类）

定义：每个数据点可以同时属于多个簇，但具有不同的隶属度（membership）。
特点：
- 数据点被赋予概率或权重来表示它属于不同簇的程度。
- 更灵活，能够处理边界模糊的数据。
算法示例：
- Gaussian Mixture Model (GMM)
- Fuzzy C-Means
应用：适用于模糊边界的任务，比如图像分割或文本主题分析。

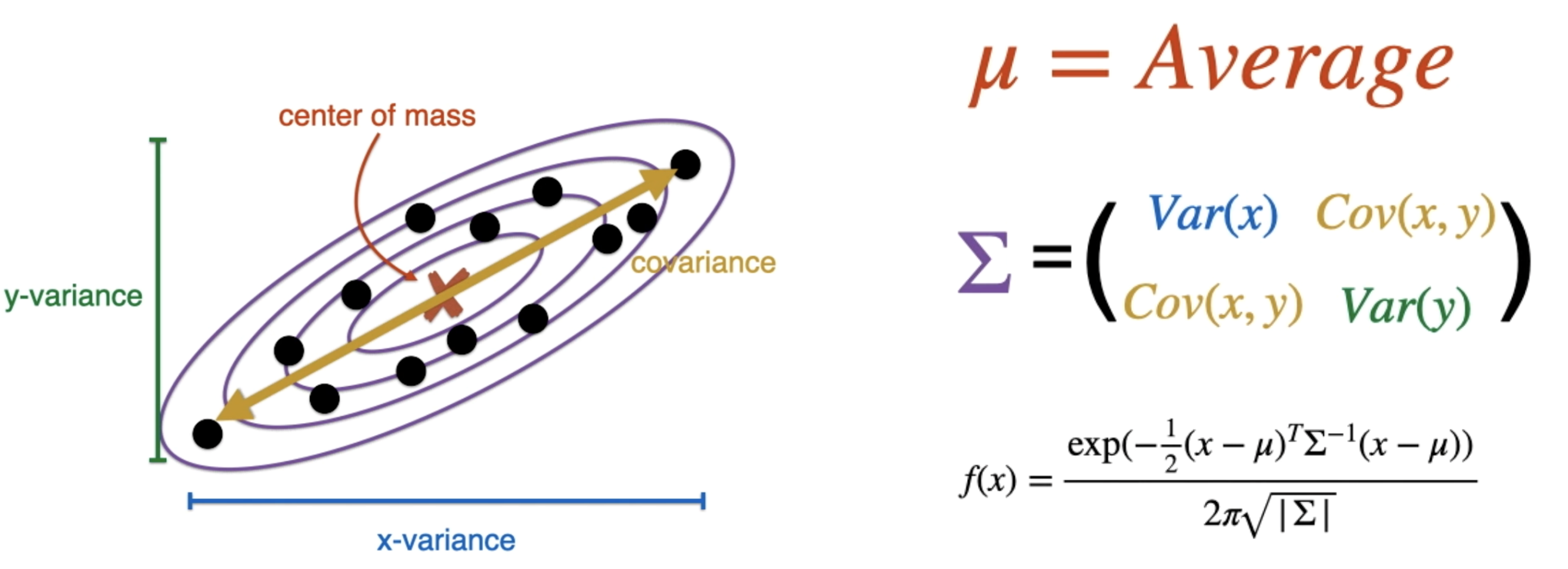
Gaussian Mixture Clustering

表示数据由 k 个高斯分布混合组成： $p_{M} (x) = \sum_{i = 1}^{k} α_{i} p (x | μ_{i}, Σ_{i})$

参数：

$α_{i}$ ：混合系数，满足 $\sum_{i = 1}^{k} α_{i} = 1$ ，且 $α_{i} > 0$ 。
$p (x | μ_{i}, Σ_{i})$ ：第 i 个高斯分布的密度函数。

步骤

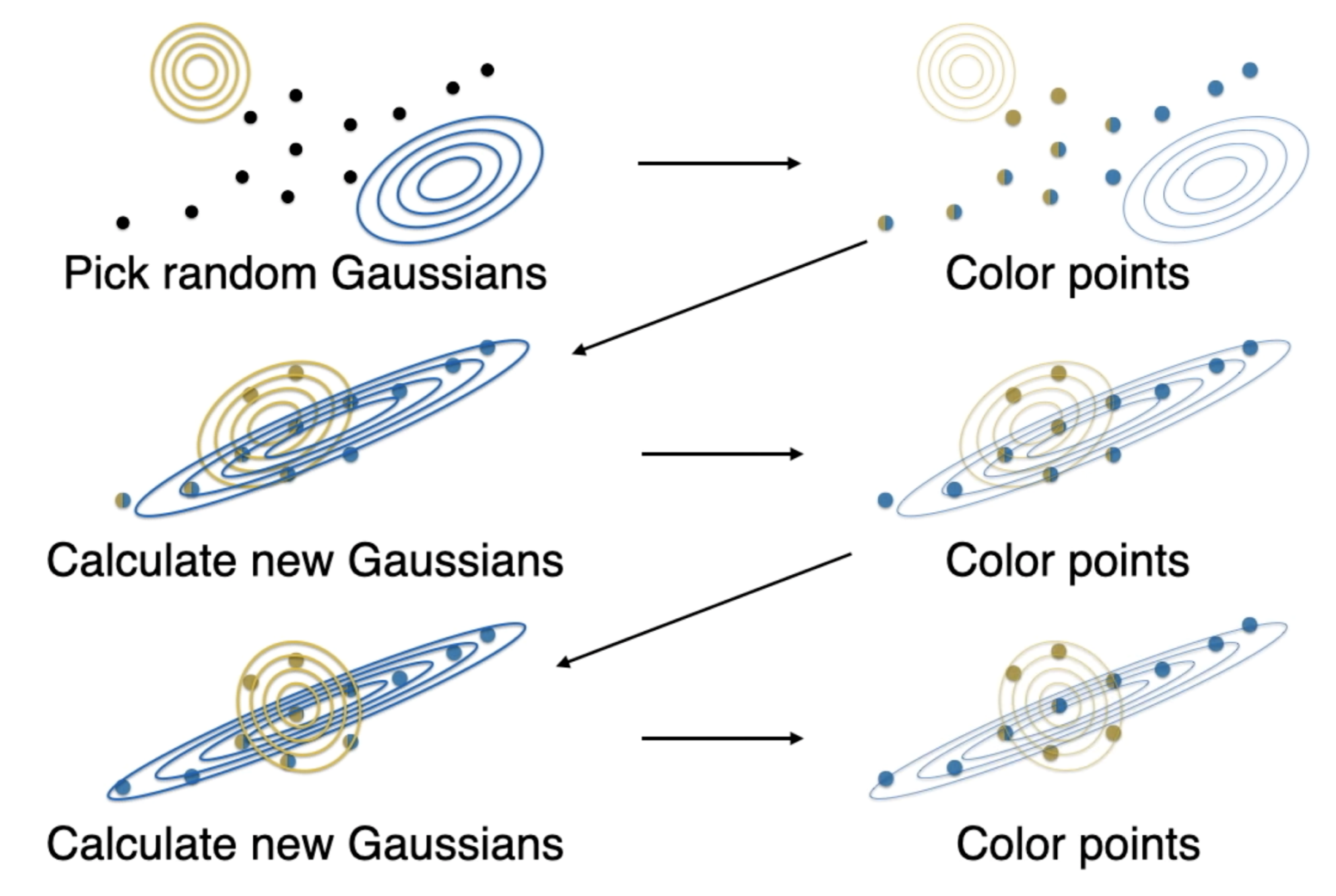
Step 1: Colouring points according to a Gaussian

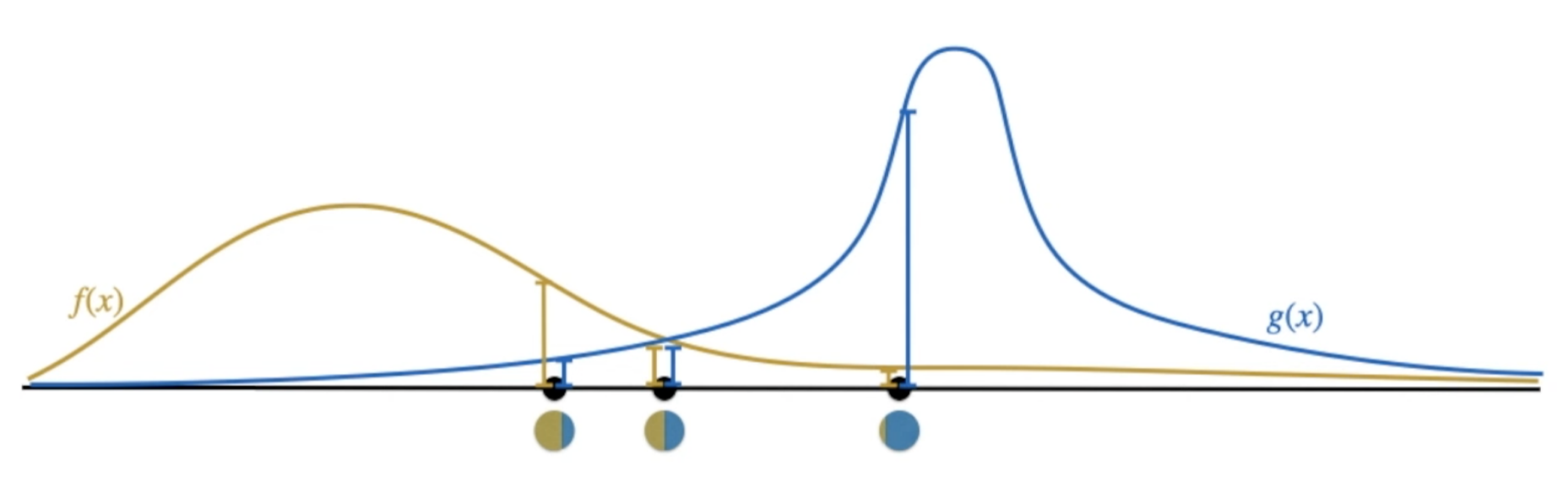
Step 2: Fitting a Gaussian

E步： 计算每个数据点对高斯分布的责任值（贡献概率）。

M步： 使用责任值更新均值、协方差矩阵和混合系数，使模型更好地拟合数据。

数据点不变，参数的更新源于模型对数据点归属的重新估计。第一步计算责任度，第二步更新均值等等。

过程图示：

Density Clustering

密度聚类定义

基于密度的聚类算法通过样本分布的紧密程度来确定聚类结构。
核心概念包括：
- 密度可达性（Density-reachable）： 样本点可以从核心点沿着高密度区域路径到达。
- 密度连通性（Density-connected）： 两个点通过密度可达的点互相连接。

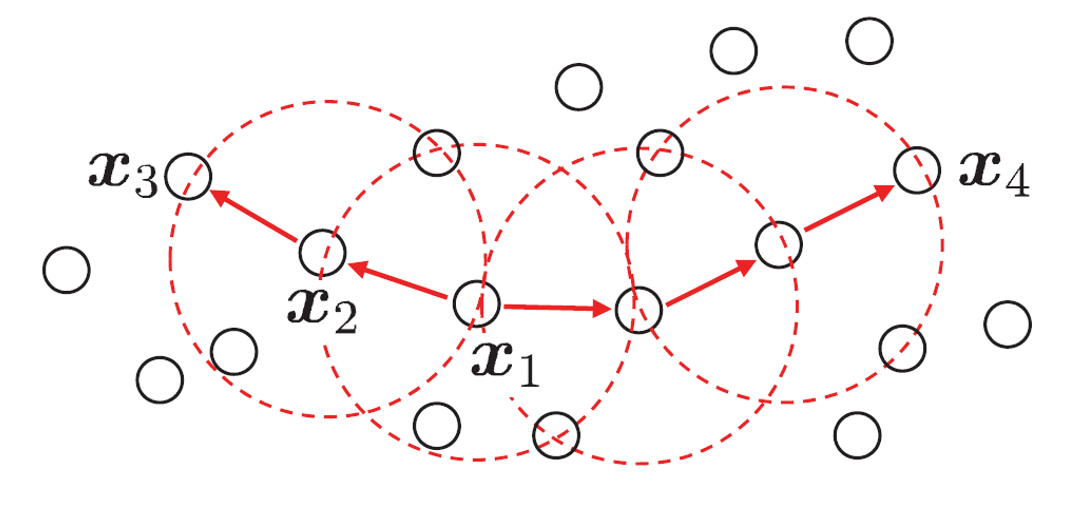
具体示例

示例中以 $M i n P t s = 3$ ，通过 $ϵ$ 范围内的点来确定核心点。
$x_{1}$ 是核心点， $x_{2}$ 和 $x_{3}$ 是密度可达点， $x_{4}$ 是密度连通点。
聚类定义为密度连通样本集。

图例

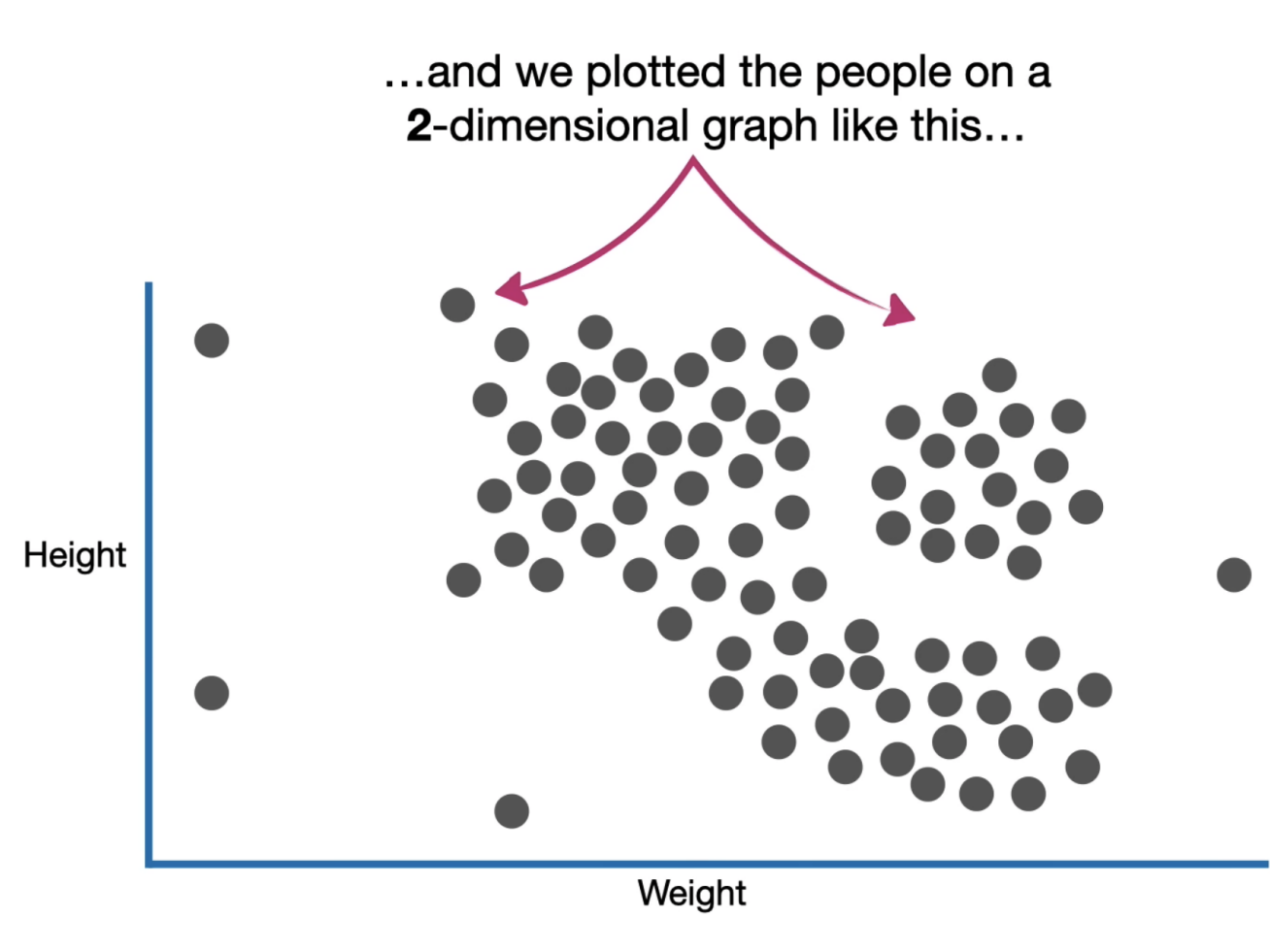
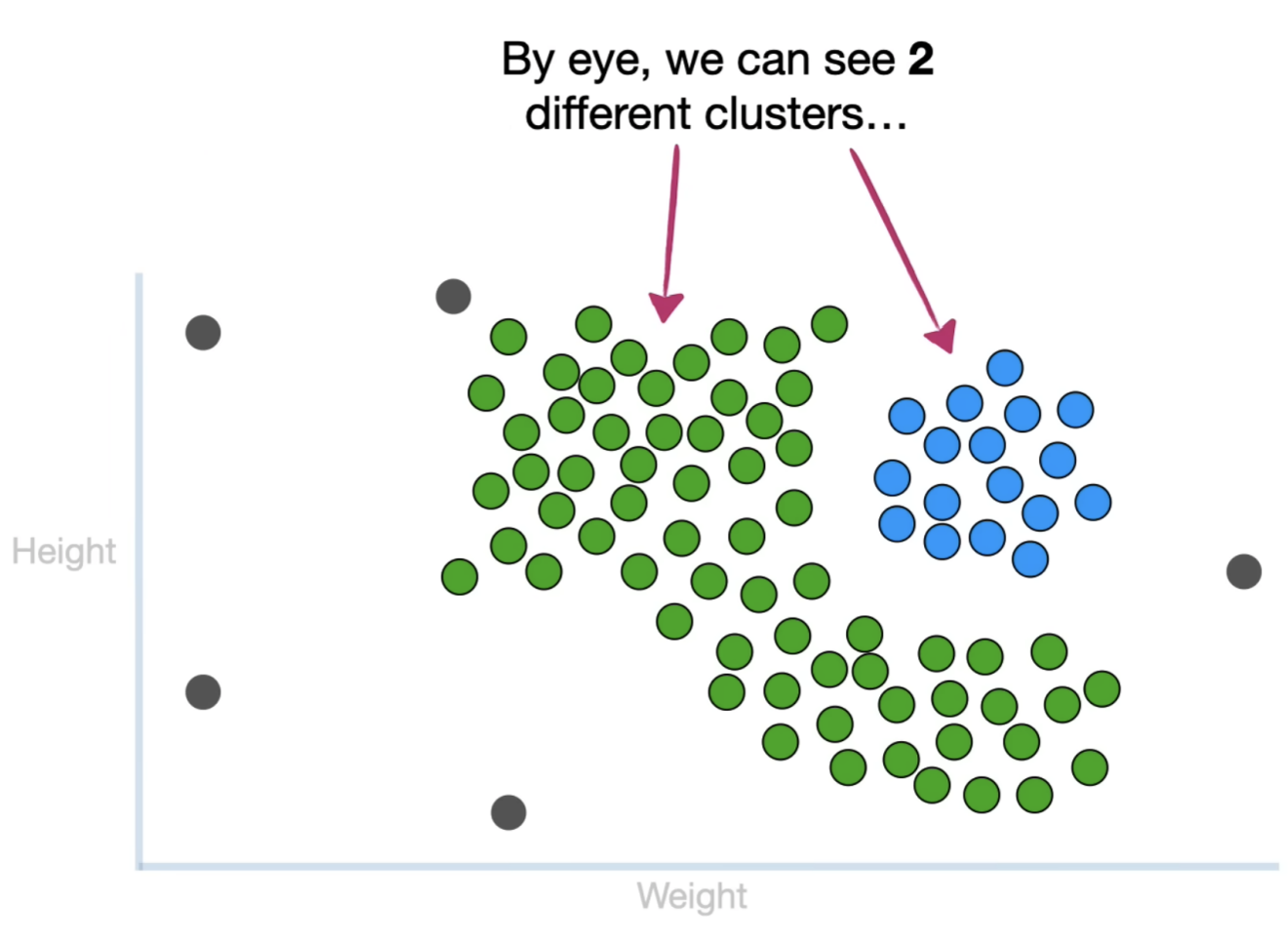
人眼可以大致分辨出数据中存在两个主要簇群（绿色和蓝色区域），说明数据点可能具有内在的分组结构。

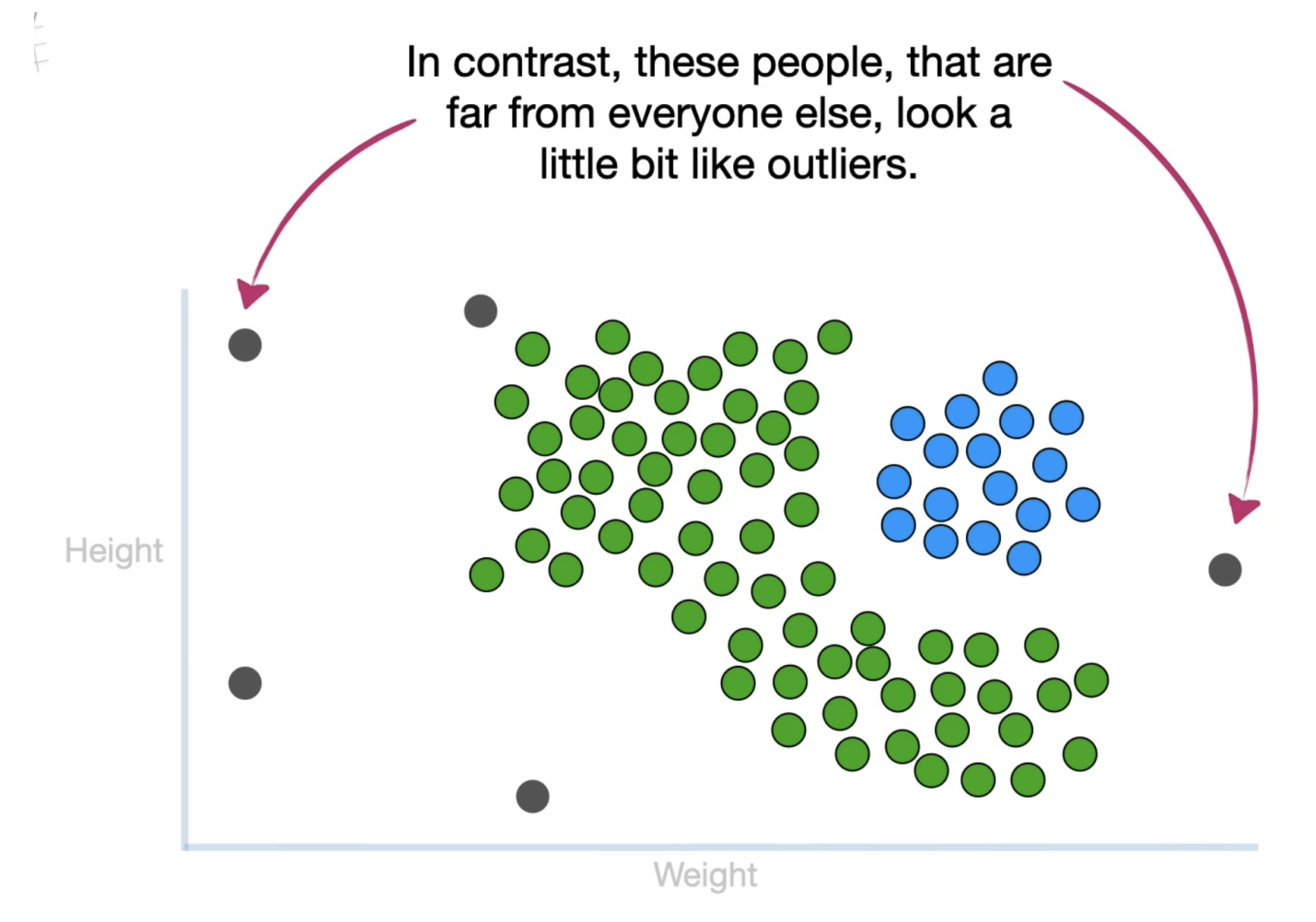
离簇群较远的灰色数据点可能是异常值或离群点，显示与其他数据点的分布存在较大偏差。

定义核心点：核心点被定义为周围至少有一定数量（如4个）其他点的点。图片中的橙色圈表示每个点的邻域范围。

识别核心点：第二张图片强调了一些点（红色点）是核心点，因为它们的邻域范围内包含了至少4个其他点。

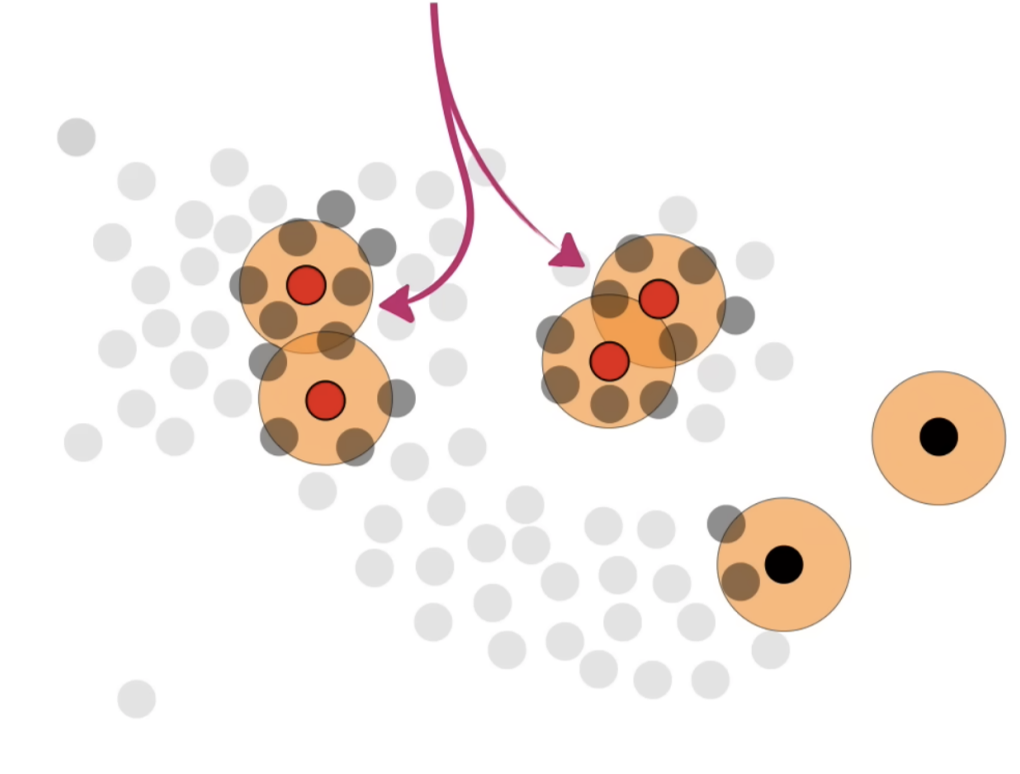
最终确定核心点集合：第三张图片显示了所有符合核心点条件的点，这些点都被标记为红色，它们构成了密度聚类中最核心的部分。

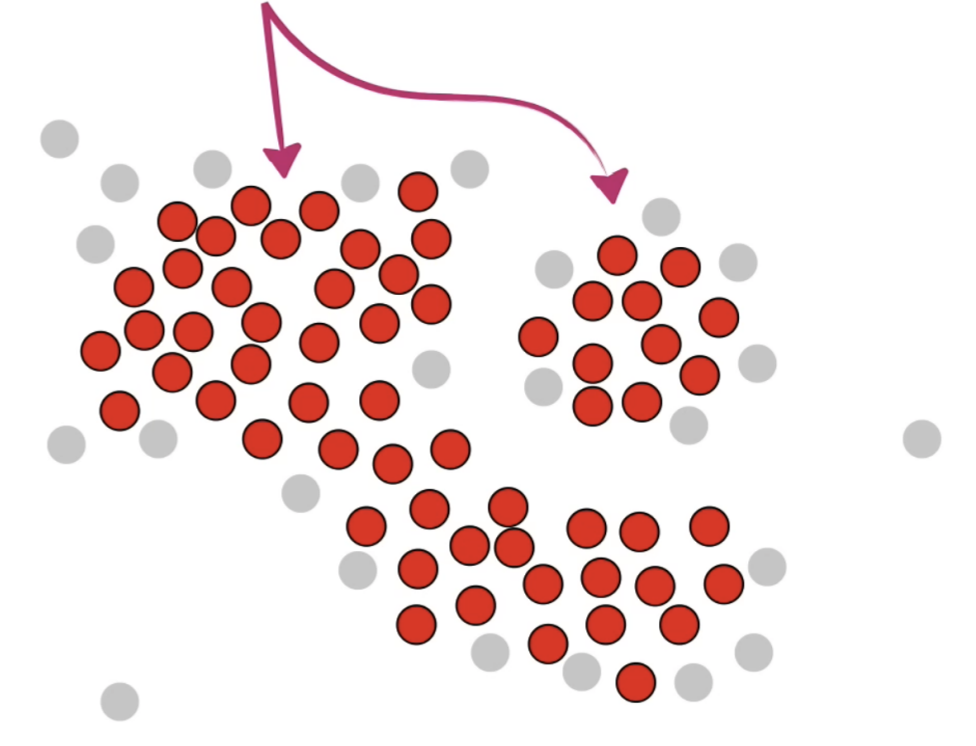
但是留下了一些六神无主的点。。。。

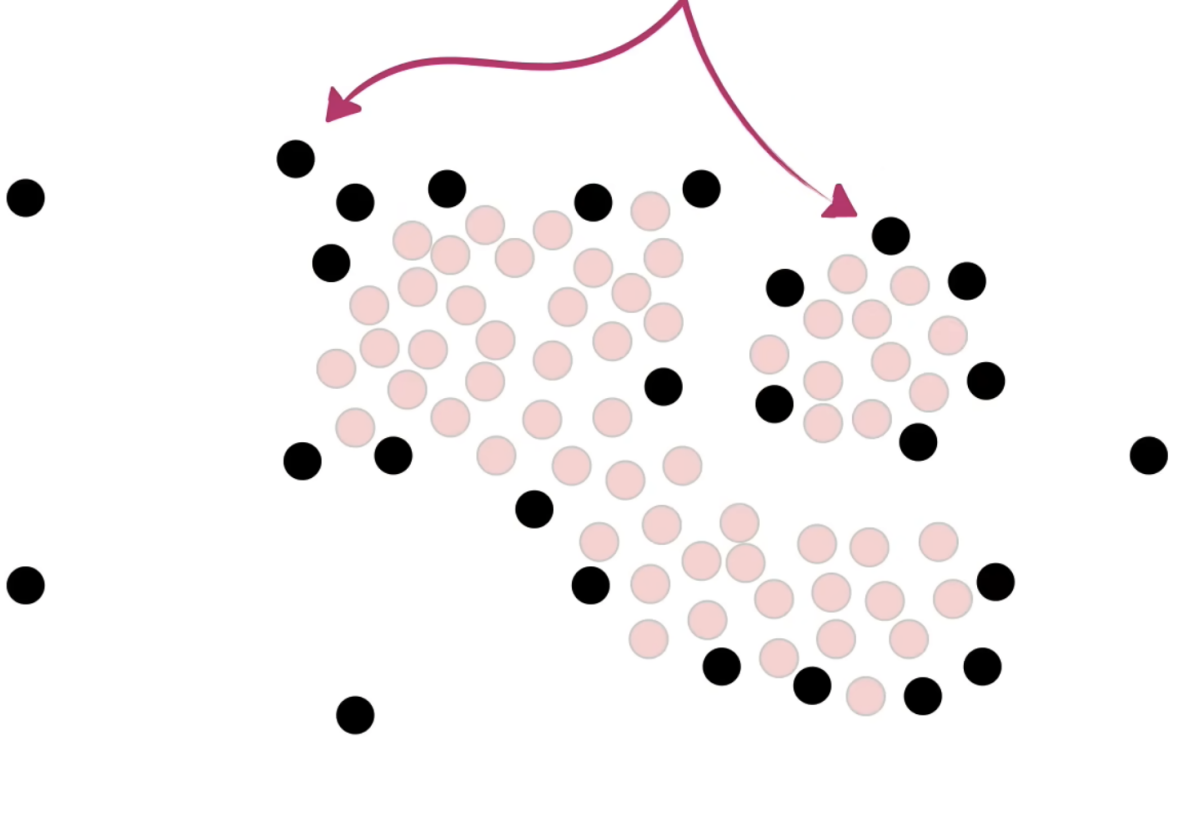
剩下的看ppt吧太多了！！

Hierarchical clustering（层次遍历）

1. 层次聚类方法：

采用树状结构表示数据的聚类过程，形成 "树状聚类结构"。
两种策略：
- 自底向上（AGNES）：从单个样本作为初始聚类，不断合并最相近的两个簇，直到达到预设的簇数。
- 自顶向下：从整体划分开始，逐步细化。

2. AGNES算法步骤：

初始时，每个样本单独作为一个簇。
每次找到两个最近的簇，合并为一个新簇。
重复以上过程，直到满足聚类停止条件。

簇间距离的计算方式：

最小距离 ( $d_{min}$ )：簇之间最短的样本点距离。
最大距离 ( $d_{max}$ )：簇之间最长的样本点距离。
平均距离 ( $d_{avg}$ )：簇之间所有样本点对距离的平均值。

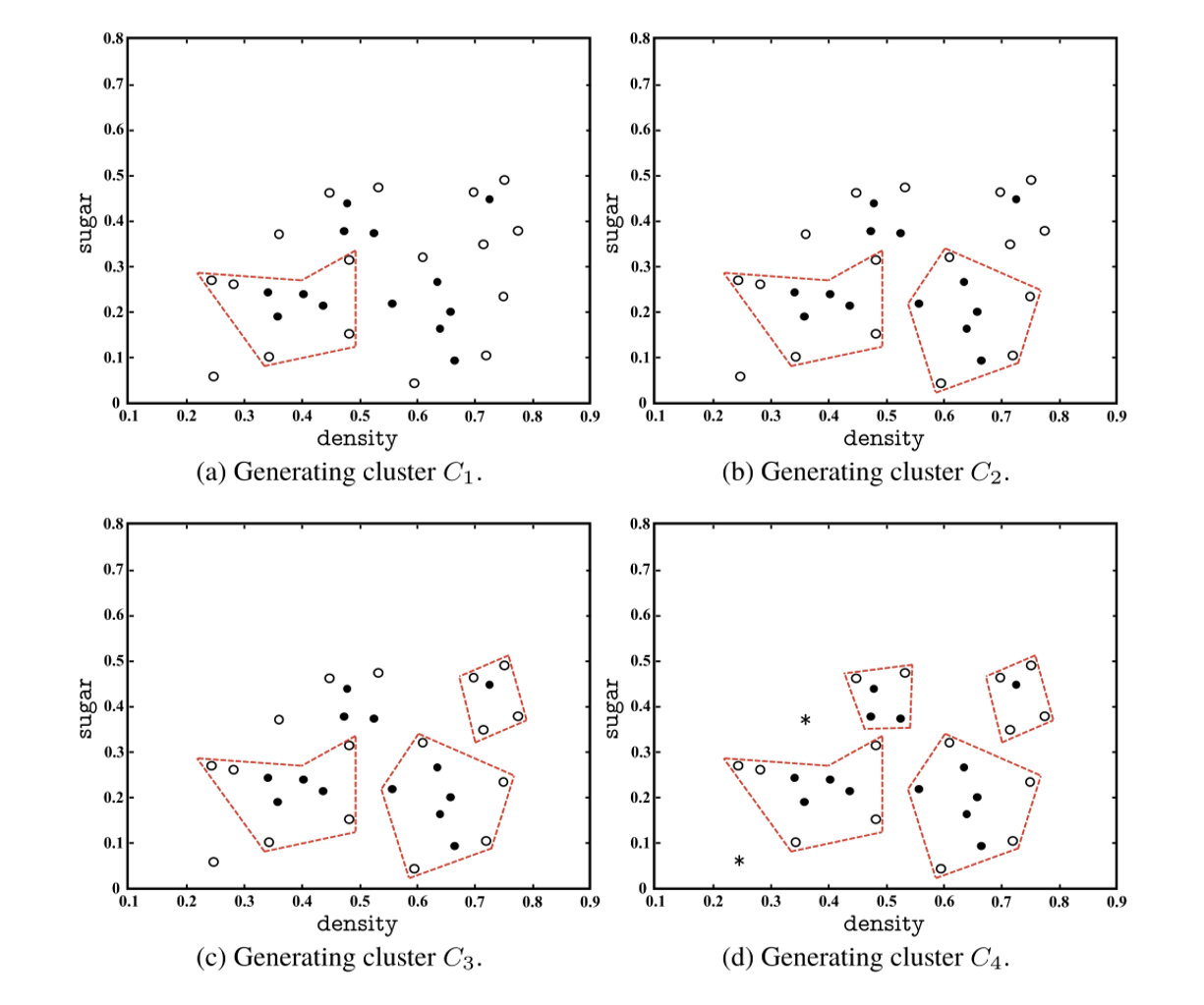
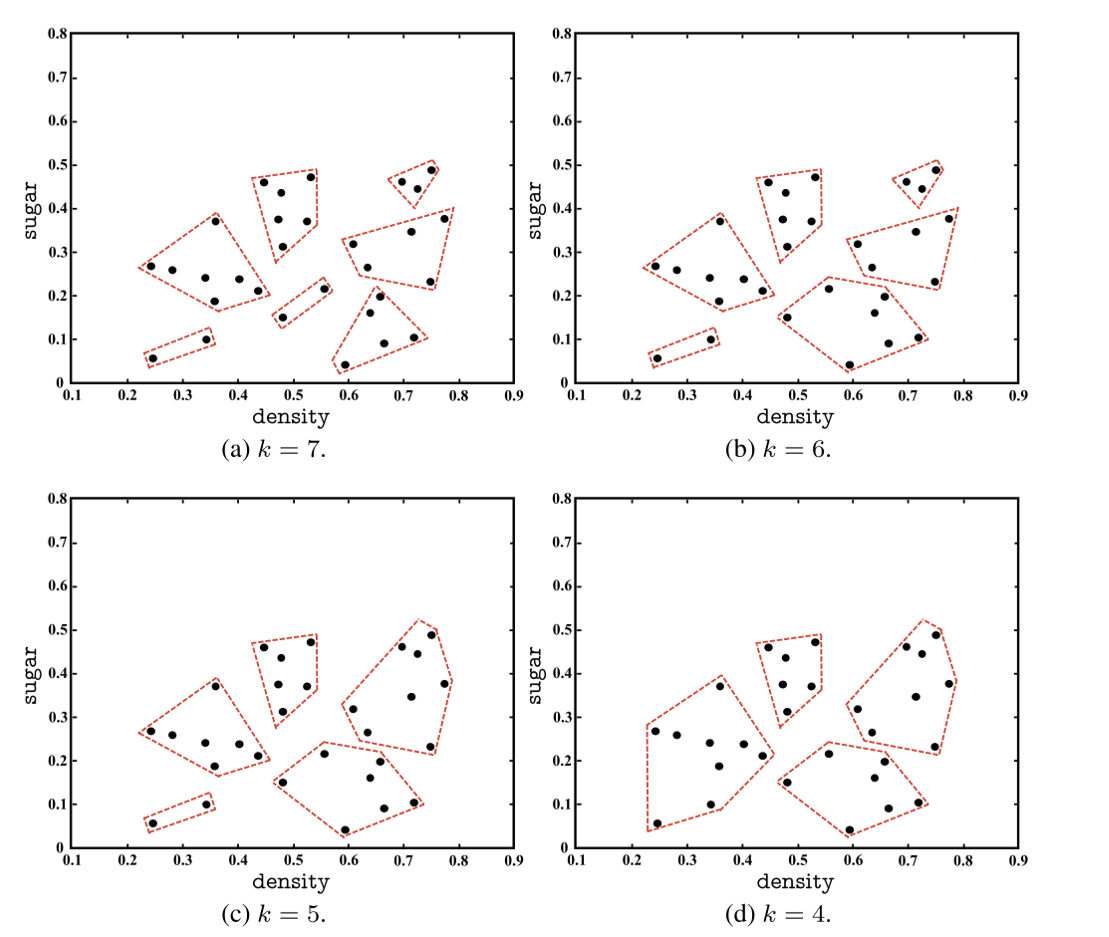
图展示了AGNES（基于层次的聚类算法）的聚类效果。通过不同的k值（即指定的最终簇的数量），展示了从细粒度的多个簇（如k=7）到更粗粒度的少数簇（如k=4）的变化。点的分组和边界的定义依赖于数据的密度和相似性。

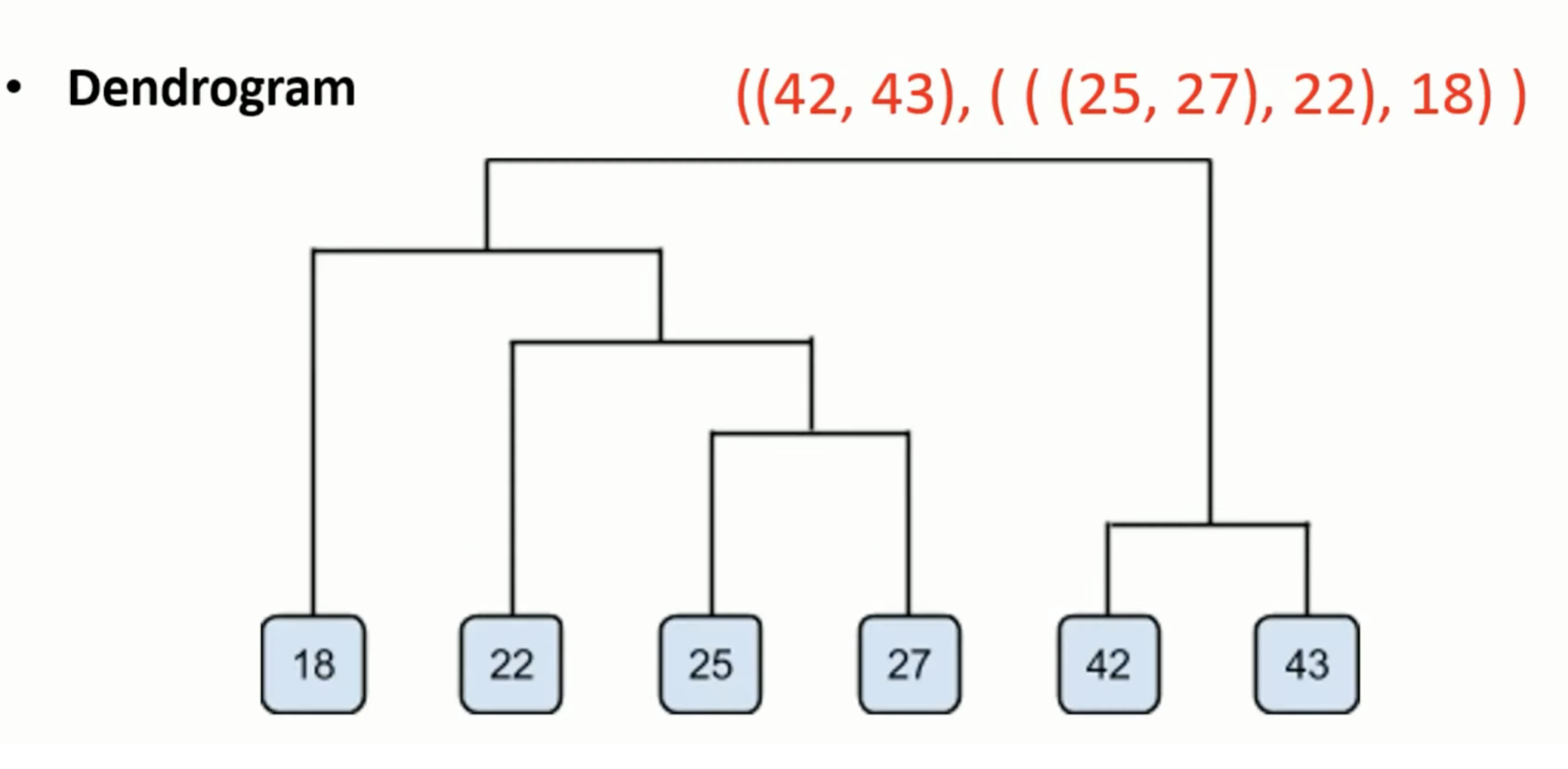
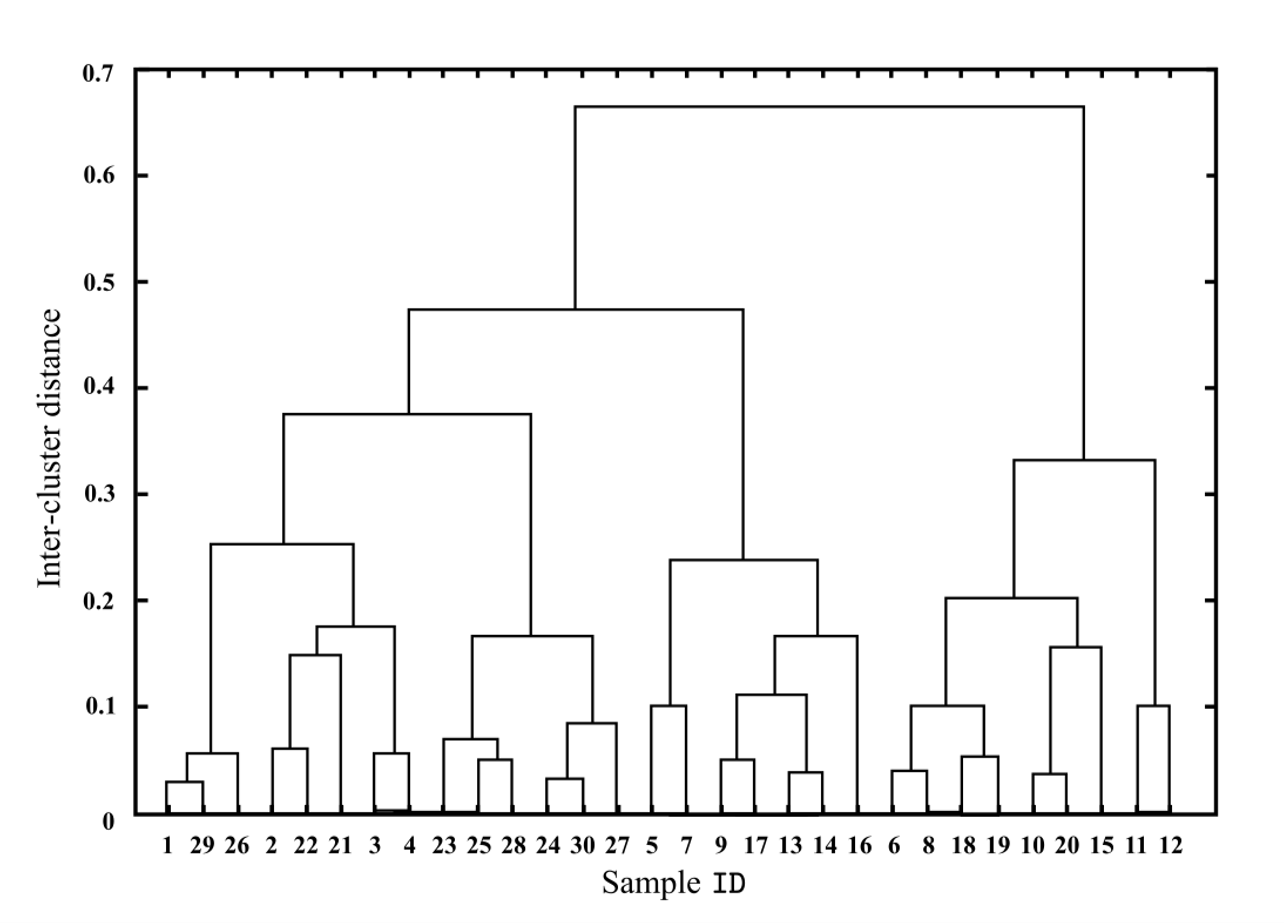
一个实例

数据点为一维值18, 22, 25, 42, 27, 43，使用了基于“最小距离”（Min Distance）的聚类方法。

初始化距离矩阵：

每个数据点被视为一个单独的簇。
矩阵中的值表示不同数据点之间的距离。

第1步：合并最接近的两个簇：

找到矩阵中最小的距离值（如42和43的距离）。
将这两个数据点合并为一个新的簇。
更新矩阵以反映新簇和其他数据点之间的距离。

第2步：继续合并最近的簇：

再次寻找矩阵中最小的距离值（如25和27）。
将其合并，并更新距离矩阵。

重复合并，直到…