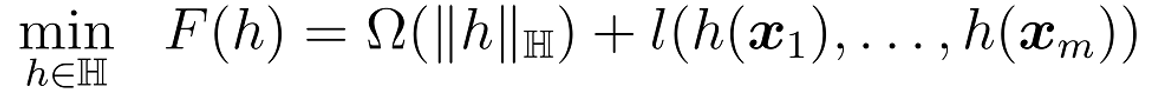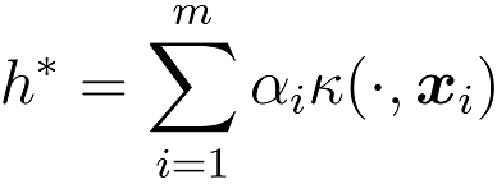机器学习第7章

Margin and Support Vector

在线性模型中，我们会发现很多个超平面可以分割两个类。如何选择这些超平面呢？

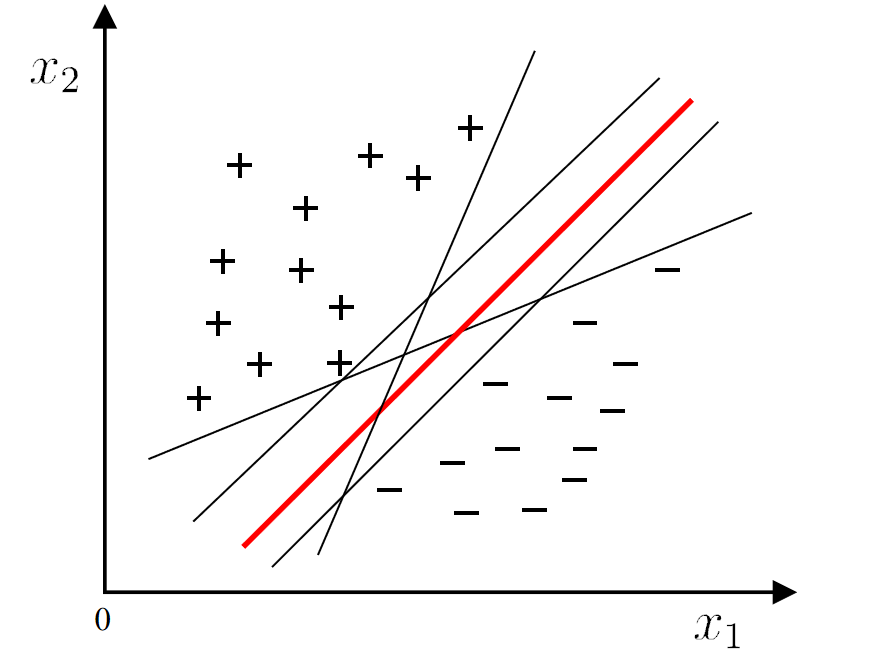
We should choose the "middle", which has good tolerance, high robustness, and the strongest generalization ability.

如何选择最优超平面

1. 超平面

超平面方程：

${\omega }^{T}x+b=0$

其中：

• $\omega$：超平面的法向量，决定超平面的方向。
• $b$：偏置项，决定超平面与原点的距离。

分类规则：

• 对于分类标签 $y_i=+1$，有 ${\omega }^T{x}_i+b>0$。
• 对于分类标签$y_i=-1$，有 ${\omega }^T{x}_i+b<0$。

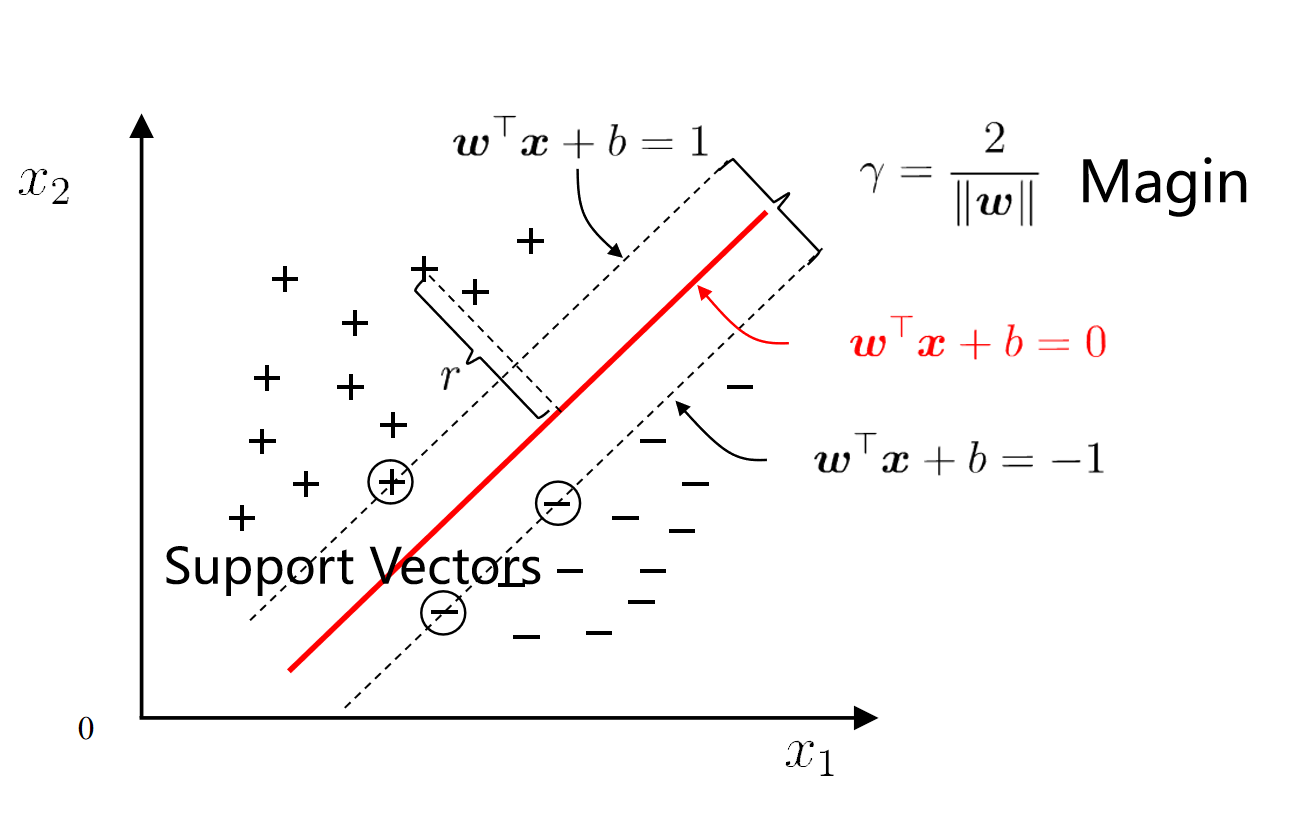
2. 间隔 (Margin)

• 定义：间隔是超平面与最近的训练样本（支持向量）之间的距离。
• 数学表达：$\gamma =\frac{2}{\parallel \omega \parallel }$ 其中 $|\omega \parallel$ 是法向量 $\omega$ 的范数。
• 最大间隔：
  • 支持向量机（SVM）的目标是找到一个超平面，使间隔 $\gamma$ 最大化。
  • 最大化间隔可以提高模型的泛化能力，减少分类错误。

3. 支持向量 (Support Vector)

• 定义：支持向量是距离超平面最近的那些数据点，它们决定了超平面的具体位置。
• 性质：
  • 支持向量位于边界线上，对应的方程为： ${\omega }^T{x}_i+b=\pm 1$
  • 这些点对超平面的定义起到关键作用，删除或修改这些点会导致超平面发生变化。

4. SVM 中的优化目标

• 最大化间隔： 为了找到最佳超平面，SVM 将间隔最大化，同时满足所有训练样本的分类约束。 原始优化问题：

  ${\text{arg max}}_{\omega ,b}\frac{2}{\parallel \omega \parallel }\text{s.t.}{y}_i({\omega }^T{x}_i+b)\ge 1,i=1,2,...,$

• 等价形式：

  转化为最小化

  $\frac{1}{2}\parallel \omega {\parallel }^2$：

  ${\text{arg min}}_{\omega ,b}\frac{1}{2}\parallel \omega {\parallel }^2\text{s.t.}{y}_i({\omega }^T{x}_i+b)\ge 1,i=1,2,...,m.$通过约束条件确保正确分类。

  • 目标函数 $\frac{1}{2}\parallel \omega {\parallel }^2$ 最小化可以最大化间隔。

Soft Margin and Regularization

1. soft margin

实际中，很难找到一个合适的核函数，使得训练样本在特征空间中线性可分。即使找到这样的核函数，也很难确定是否是过拟合导致的。

引入**软间隔（Soft Margin）**的概念，允许支持向量机对某些样本不满足约束或出现错误。

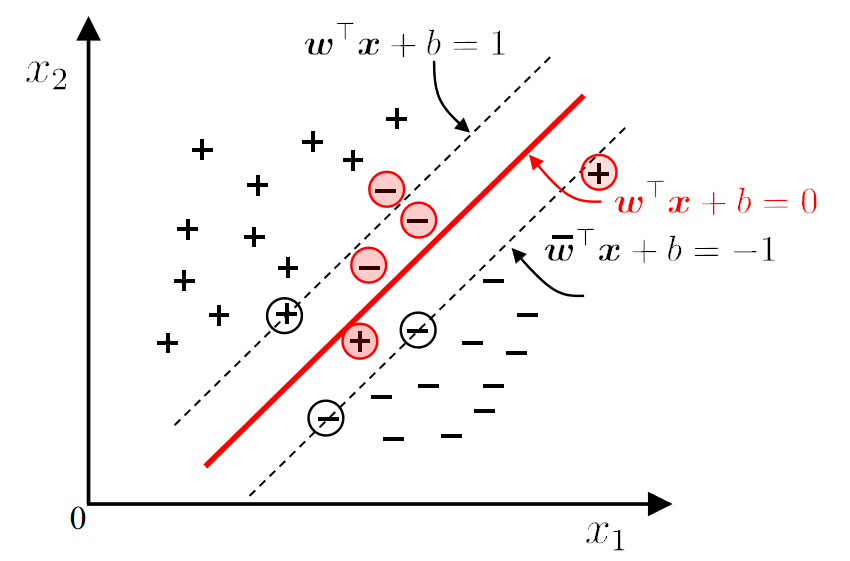
基本思想：在最大化间隔的同时，尽量减少不满足约束的样本数量。

目标函数： $\underset{w,b}{min}\frac{1}{2}\parallel w{\parallel }^2+C\sum _{i=1}^m{l}_{0/1}(y_i(w^T\varphi (x_i)+b)-1)$

其中$C>0$ 是常数，$l_{0/1}$ 为0/1损失函数。

注

• C是超参数，决定正则化项和误分类损失之间的权衡：
  • C 大时：模型更关注分类准确率（可能会过拟合）。
  • C 小时：模型更关注间隔最大化（可能会欠拟合）。

问题：0/1损失函数是非凸、不连续的，难以优化。

2. replacement

$l_{0/1}$

z 表示样本点是否满足约束条件，例如 $z=y_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b)-1$。

0/1 损失的作用：

• $z<0$：样本点未满足 $y_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b)\ge 1$ 的间隔约束（即分类错误或违反硬间隔），此时损失为 1。
• $z\ge 0$：样本点满足分类约束，损失为 0。

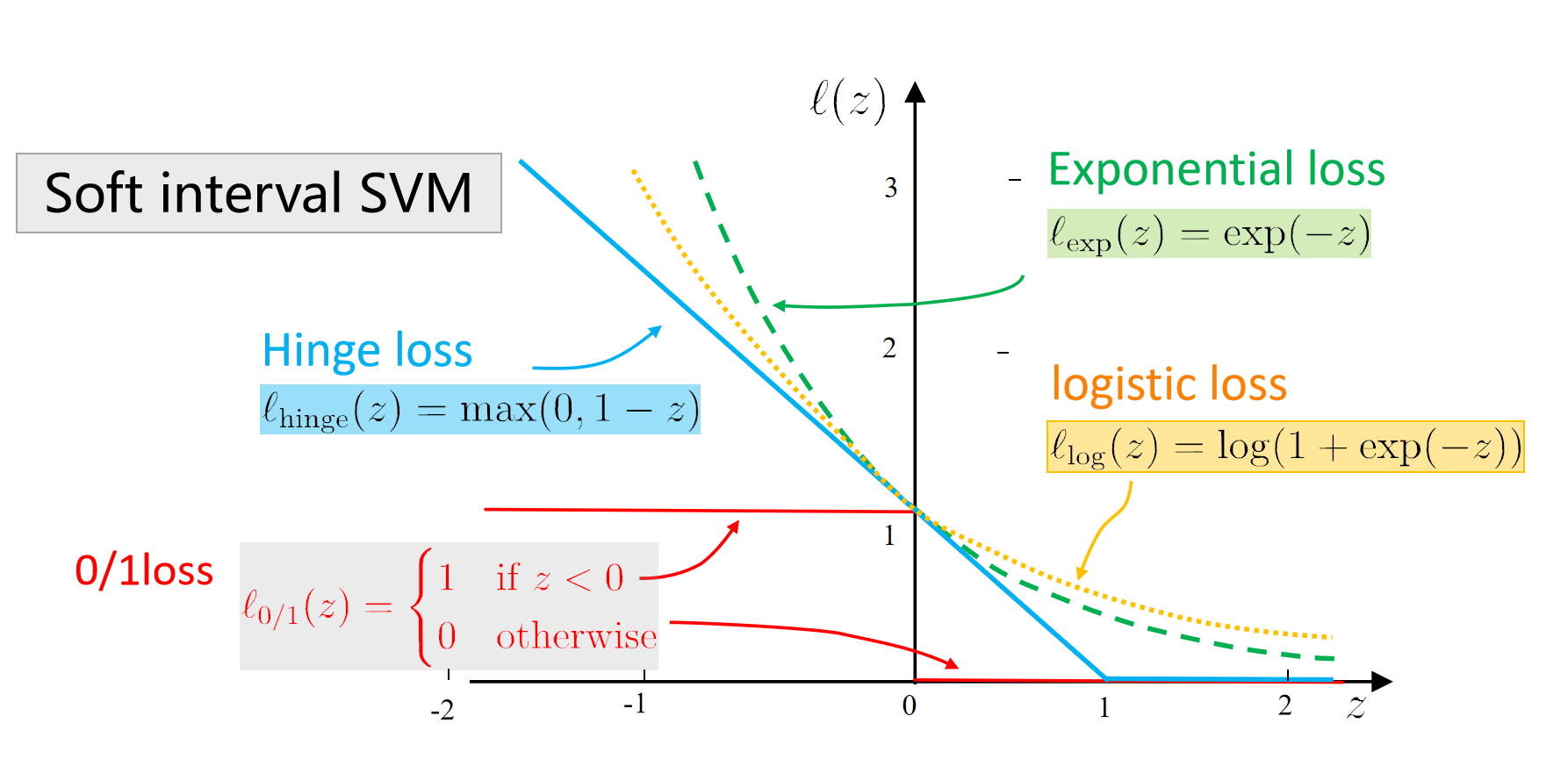
替代损失函数在数学性质上更好，且通常是0/1损失函数的上界。

3. 松弛变量

$y_i$：标签，用于保证样本的分类正确：

• 当 $y_i=+1$，约束变为 ${\omega }^T{x}_i+b\ge 1-{\xi }_i$。
• 当$y_i=-1$，约束变为 ${\omega }^T{x}_i+b\le -1+{\xi }_i$。

新的优化目标变为：

$\underset{\omega ,b,{\xi }_i}{min}\frac{1}{2}\parallel \omega {\parallel }^2+C\sum _{i=1}^m{\xi }_i$

$s.t.y_i({\omega }^T{x}_i+b)\ge 1-{\xi }_i,{\xi }_i\ge 0$

• 第一项：$\frac{1}{2}\parallel \omega {\parallel }^2$ 用于最大化超平面间隔。
• 第二项：$\sum {\xi }_i$ 表示违反约束的惩罚项（误分类或在间隔内的样本）。
• C：超参数，用于平衡间隔大小和违反约束的惩罚之间的权重。

${\xi }_i$：松弛变量，允许少量样本违反间隔约束。

如果没有松弛变量就是硬间隔。

4. Regularization

$\underset{f}{min}\mathrm{\Omega }(f)+C\sum _{i=1}^{m}l(f(x_i),y_i)$

1. $\mathrm{\Omega }(f)$ - 结构风险（Structural Risk）：
   • 表示模型的复杂度，用来描述模型的一些特性。
   • 目标：限制模型复杂度，防止过拟合。
   • 例如：L2正则项（权重平方和）、L1正则项（权重绝对值和）。
2. $\sum _{i=1}^{m}l(f(x_i),y_i)$ - 经验风险（Empirical Risk）：
   • 通过损失函数 lll 衡量模型在训练数据上的误差。
   • 目标：确保模型能够很好地拟合训练数据。
   • 例如：
     • 逻辑回归的对数损失
     • SVM 的 Hinge 损失
3. C - 平衡系数：
   • 调整结构风险和经验风险之间的权衡。
   • C 越大，模型更注重拟合数据（降低经验风险）；C 越小，模型更注重简单性（降低结构风险）。

公式目的：

目标：最小化结构风险 + 经验风险。

平衡两者的关系（通过 C 控制）：

• 如果 C 很大，模型会更注重拟合数据，减少误差，但可能导致过拟合。
• 如果 C 很小，模型会更注重简单性，可能导致欠拟合。

Kernel function

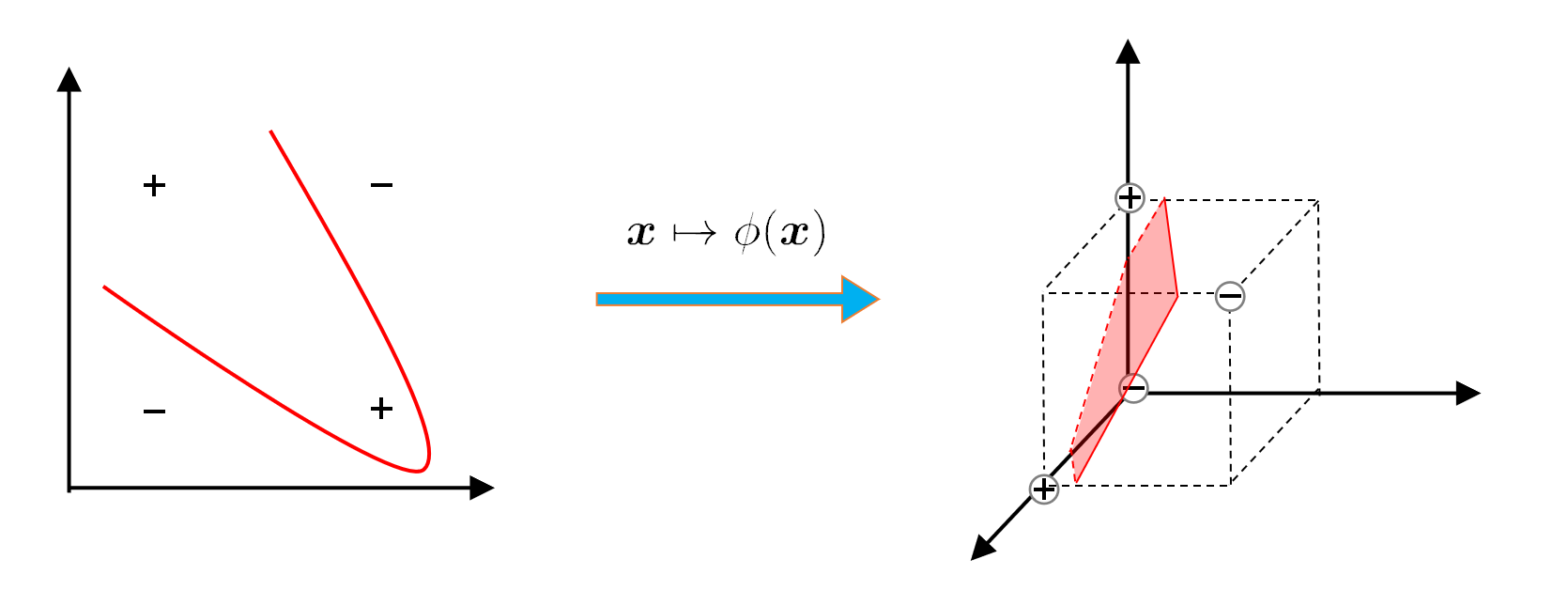
• Q: What if there is no hyperplane that can correctly divide the two types of samples??
• A: Map the samples from the original space to a higher-dimensional feature space so that the samples are linearly separable in this feature space.

1. 核函数的作用

核函数的主要作用是将数据从低维空间映射到高维空间，从而使得在高维空间中找到一个线性可分的超平面进行分类。

• 原始问题中，样本 x 通过映射函数 $\varphi (x)$ 映射到高维空间。
• 核技巧：直接使用核函数 $\kappa (x_i,x_j)$，避免显式计算映射后的向量 $\varphi (x)$。 $\kappa (x_i,x_j)=⟨\varphi (x_i),\varphi (x_j)⟩=\varphi (x_i{)}^T\varphi (x_j)$

2. Mercer 定理与核函数选择

• Mercer 定理：如果核函数对应的核矩阵是半正定的（semi-positive definite），那么该函数可以作为合法的核函数。
• 原因：核矩阵的半正定性保证了在高维空间中定义的内积是有效的。

简单理解： 一个核函数能够确保映射到高维空间的计算是合理且有效的。

3. 常见的核函数

Dual Problem

拉格朗日到对偶问题

拉格朗日

简化计算： 原始问题需要直接优化 $\omega$ 和 b，而对偶问题仅涉及拉格朗日乘子 ${\alpha }_i$​，简化了计算。

相关信息

约束条件的引入：$-\sum _{i=1}^n{\alpha }_i(y_i({\mathbf{w}}^{\mathrm{\top }}{\mathbf{x}}_i+b)-1)$

• 这一项通过拉格朗日乘子 ${\alpha }_i$ 将间隔条件 $y_i({\mathbf{w}}^{\mathrm{\top }}{\mathbf{x}}_i+b)\ge 1$ 融入目标函数。
• 物理意义：
  • 拉格朗日乘子 αi\alpha_iαi 用于衡量每个样本点对最终分类超平面约束的贡献。
  • 当 $y_i({\mathbf{w}}^{\mathrm{\top }}{\mathbf{x}}_i+b)\ge 1$ 成立时，样本点位于正确分类区域，${\alpha }_i$ 可以取零（不影响目标函数）。
  • 如果约束不满足，${\alpha }_i$ 会增大，从而使目标函数的值受到惩罚，迫使模型调整 $\mathbf{w}$ 和 b 以满足约束条件。

对偶问题

简化求解：将复杂的带约束问题转化为对偶形式，降低求解难度。

引入核函数： 在对偶问题中，输入向量 $x_i$​ 和 $x_j$ 之间的内积$x_i^T{x}_j$可以用核函数替代，从而处理非线性数据。

稀疏性： 由于大部分拉格朗日乘子 ${\alpha }_i$​ 等于0，只有支持向量对应的 ${\alpha }_i$​ 不为0，这使得计算高效。

解决对偶问题：

Support Vector Regression

允许模型输出与实际输出之间存在一个 $2ϵ$ 的偏差。

Loss function

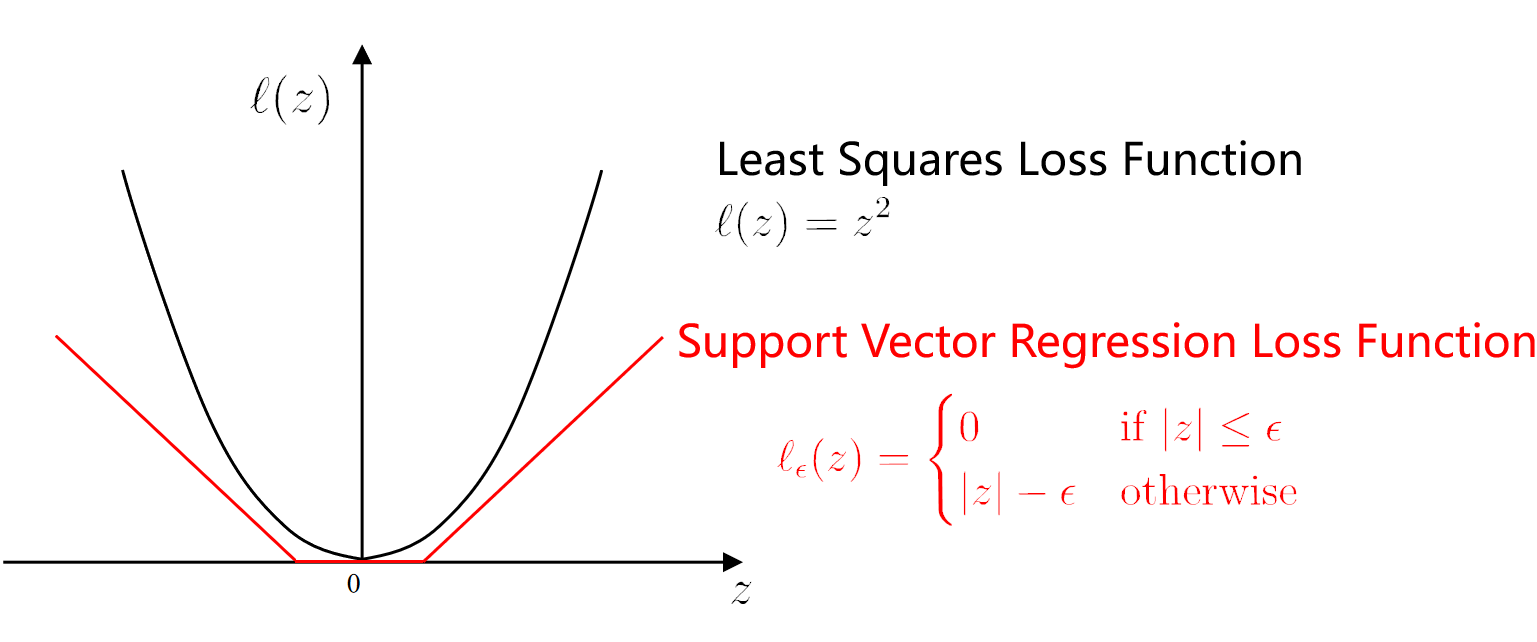
1. 最小二乘损失函数 (Least Squares Loss Function)

• 公式：$\ell (z)=z^2$
• 特点：
  • 对所有偏差都计算平方损失。
  • 在训练过程中，所有误差都会被考虑。
  • 对异常值（Outliers）较敏感，因为较大的偏差会导致损失剧增。
  • 损失函数曲线是二次函数，对称且无阈值。

2. 支持向量回归的 $ϵ$-不敏感损失函数

• 公式：

  ${\ell }_{ϵ}(z)=\{\begin{array}{ll}0& \text{if }|z|\le ϵ\\ |z|-ϵ& \text{otherwise}\end{array}$

  • 其中 $ϵ$ 是一个设定的阈值。

• 特点：

  • 当误差 $|z|$ 在 $[-ϵ,ϵ]$ 区间内时，不计算损失
  • 当误差超过 $ϵ$ 时，损失是 $|z|-ϵ$，线性增加。
  • 2$ϵ$ 间隔带：使得一部分样本点的误差被忽略，有助于模型的稀疏性和泛化能力。

• 优势：

  • 忽略小偏差，使得模型对细小的误差不敏感。
  • 通过调整 $ϵ$，可以控制模型的拟合程度和复杂度。
  • 使支持向量回归在保证准确度的同时，模型解具有稀疏性（少数支持向量决定模型）。

原始问题

函数

约束条件

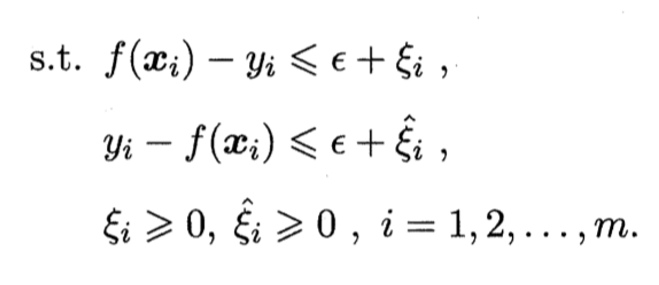
• 松弛变量 ${\xi }_i$ 和 ${\hat{\xi }}_i$：
  • 用于处理超出 $ϵ-$不敏感区间的数据点。
  • 几何意义：这些变量允许一定程度的误差存在，使得模型对异常值具有一定的鲁棒性。

拉格朗日，增加稀疏性

image-20241217153227633

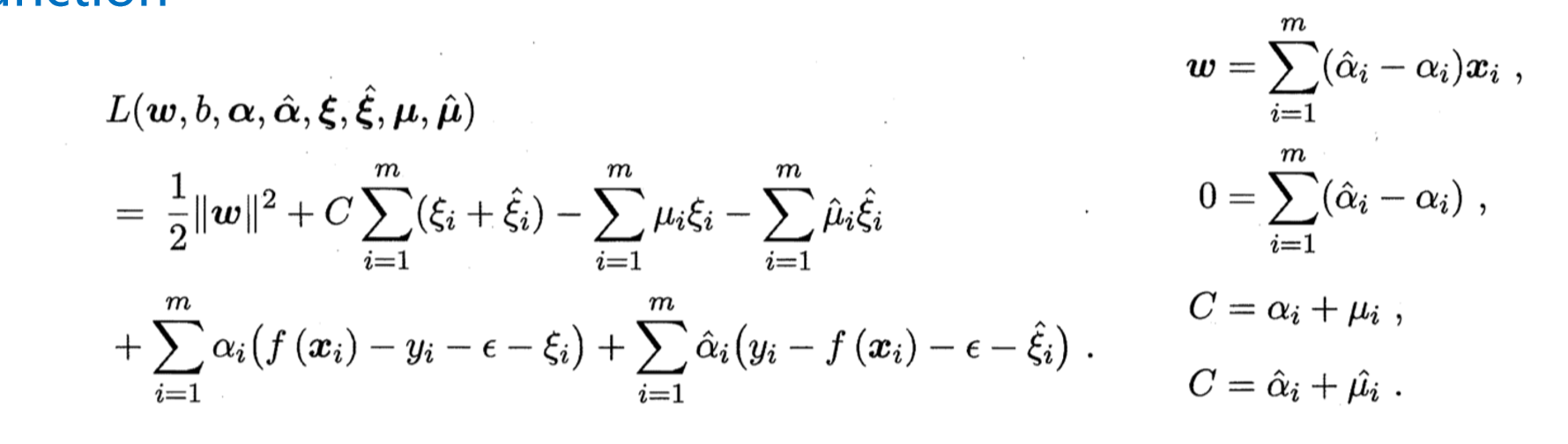
对偶，简单化

最终回归模型

通过对偶问题的解 ${\alpha }_i,{\hat{\alpha }}_i$，最终的回归模型可以表示为：

$f(x)=\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)x_i^{T}x+b$

• 支持向量：只有满足 ${\alpha }_i>0$ 或 ${\hat{\alpha }}_i>0$ 的样本点才参与最终模型计算。
• b：偏置项，由支持向量确定。
• 最终回归模型只依赖于支持向量，具有稀疏性，提高了计算效率。

Kernel Methods

The solution to the optimization function can always be written as