机器学习第8章

XiaoXianYue原创2024年12月17日大约 10 分钟

Basic Process

tree structure

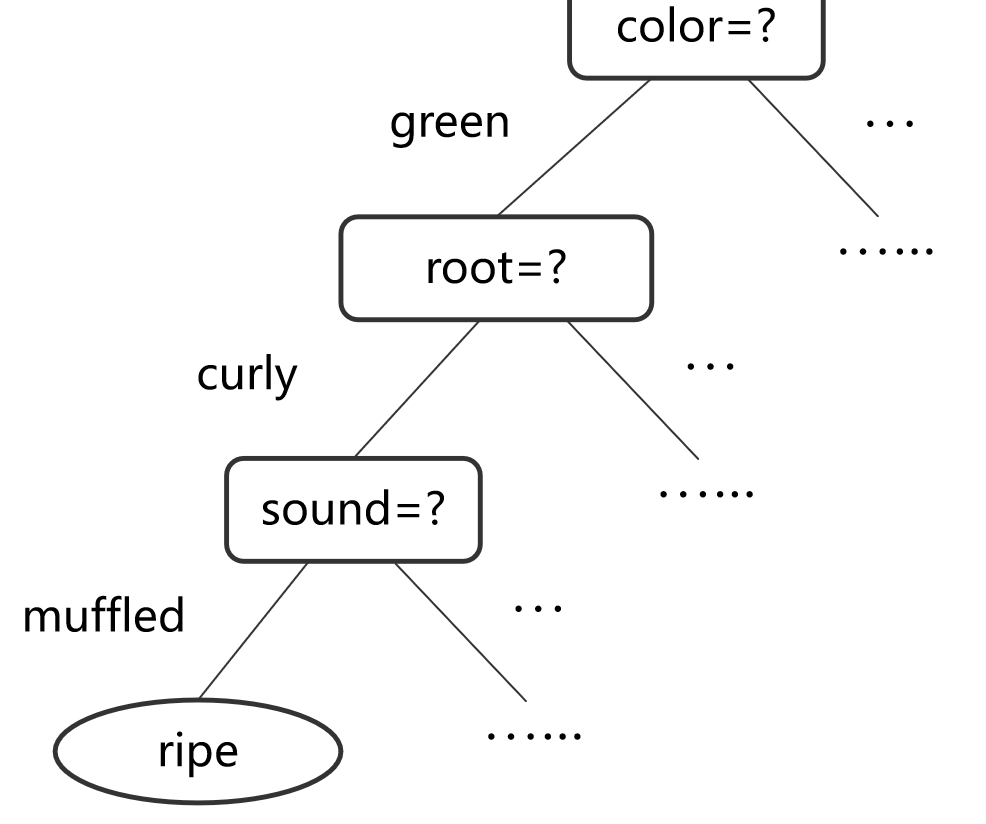
决策树的结构：

使用树形结构进行预测。
每个节点代表一个决策规则（如 "if-then-else" 规则），每个分支代表一个判断分支，叶节点给出最终的类别或数值预测。

流程：

从根节点开始，根据特征值进行分裂，按照“if-then-else”规则递归地进行决策。
通过分支（branching）将数据逐步分类或回归。

优缺点

优点（Pros）：

可解释性强：决策树简单直观，便于理解，易于解释。
特征适用广泛：可以处理数值型和分类型特征。
非线性模型：能够解决非线性问题。

缺点（Cons）：

不稳定性：决策树对数据噪声较敏感，容易导致模型不稳定（可通过集成学习方法如随机森林解决）。
过拟合问题：复杂树结构容易过拟合，需要进行剪枝（prune）。
计算复杂度：决策树训练过程中不易并行化，计算效率较低。

Split Selection

1. 如何选择最佳属性？

目标：选择最优的属性来生成最紧凑的分支，从而提高决策树的分类性能。
核心思想：希望决策树每个分支节点中的样本尽量属于同一类别，即节点的“纯度”尽量高。
常用的属性分裂方法：
- 信息增益（Information Gain）
- 增益率（Gain Ratio）
- 基尼指数（Gini Index）

2. 信息熵与纯度的关系

信息熵（Information Entropy）是衡量数据纯度的指标：
$E n t (D) = - \sum_{k = 1}^{| Y |} p_{k} \log_{2} p_{k}$
其中：
- $p_{k}$ ：类别 $k$ 的概率。
- $Ent (D)$ ：数据集 $D$ 的信息熵。
熵的性质：
- 熵越小，数据集的纯度越高。
- 当熵为 0 时，数据集完全纯净（所有样本属于同一类别）。
- 熵的最大值为 $\log_{2} | Y |$ （均匀分布时）。

3. 信息增益的计算

信息增益衡量了分裂前后数据集的“纯度提升”：
$Gain (D, a) = Ent (D) - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} Ent (D^{v})$
其中：
- $Ent (D)$ ：分裂前数据集 D 的信息熵。
- $\frac{| D^{v} |}{| D |}$ ：分裂后每个分支节点 $D^{v}$ 的权重（占整体样本的比例）。
- $Ent (D^{v})$ ：分裂后节点 $D^{v}$ 的信息熵。
信息增益的直观意义：
- 信息增益越大，表示分裂后节点纯度提升越明显，该属性越适合用于分裂。
- 决策树算法如 ID3 使用信息增益作为分裂标准。
问题：信息增益会偏向选择取值数量较多的属性作为分裂标准。
- 例如，若有一个属性 "编号"（如1-17）用于分裂，每个值都唯一，信息增益会很高，但这样的分裂缺乏泛化能力，无法有效预测新样本。

4. 增益率

增益率 通过引入 固有值（Intrinsic Value, IV） 来调整信息增益，公式为：

$Gain_ratio (D, a) = \frac{Gain (D, a)}{IV (a)}$

其中固有值：

$IV (a) = - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} \log_{2} \frac{| D^{v} |}{| D |}$

$IV (a)$ ：反映了属性 a 的取值数量。
V：属性 a 的不同取值数量。

优点：增益率可以解决信息增益偏好取值数量多的属性的问题。

问题：增益率会偏向选择取值数量较少的属性，这同样可能导致分裂不合理。

例子

5. 基尼指数

定义

最小基尼

实例

Pruning

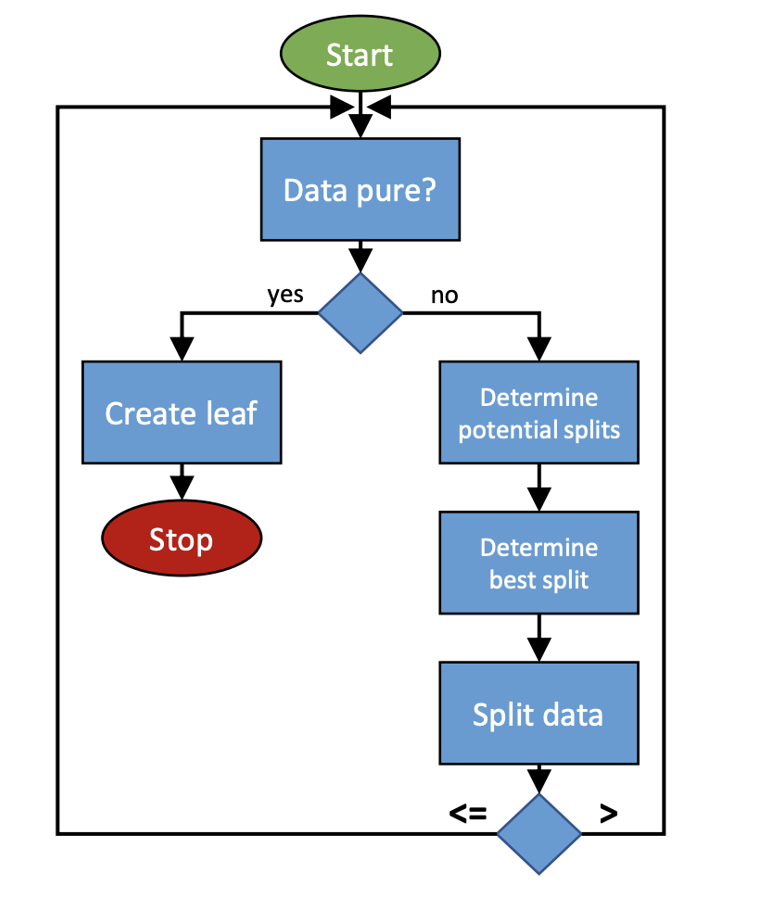
流程图：

先检查数据是否纯净，如果纯净则生成叶节点；
如果不纯净，则继续分裂数据，直到满足停止条件。

Basic pruning strategies

（1）预剪枝（Pre-pruning）

定义：在构建决策树的过程中，提前停止分裂，防止树生长过深。
方法：在每次分裂时，通过评估分裂的效果（如信息增益、基尼指数）与验证集性能，决定是否继续分裂。
优点：能够有效防止树过度生长，减少过拟合。
缺点：可能会过早停止，导致决策树欠拟合（Underfitting）。

（2）后剪枝（Post-pruning）

定义：先完全构建决策树（包括所有分裂），然后通过回溯的方式去掉不必要的分支。
方法：
1. 评估子树与叶节点的性能（如基于验证集的误差率）。
2. 如果替换子树为叶节点后性能提升或没有显著下降，则进行剪枝。
优点：可以最大程度地利用训练数据，减少欠拟合的风险。
缺点：需要额外的计算开销

如何评估剪枝效果？

评估方法：使用验证集（Validation Set）来评估决策树的泛化性能。
- 将数据分为训练集和验证集。
- 比较剪枝前后决策树在验证集上的表现。
目标：通过剪枝使决策树的泛化性能提高，减少过拟合现象。

Pre-pruning

预剪枝决策过程

核心逻辑：在决策树分裂前，判断分裂是否可以显著提高验证集的泛化性能.
- 如果分裂后的验证集准确率提高，则继续分裂；
- 如果分裂后的验证集准确率不提高或下降，则停止分裂，将当前节点设为叶节点。

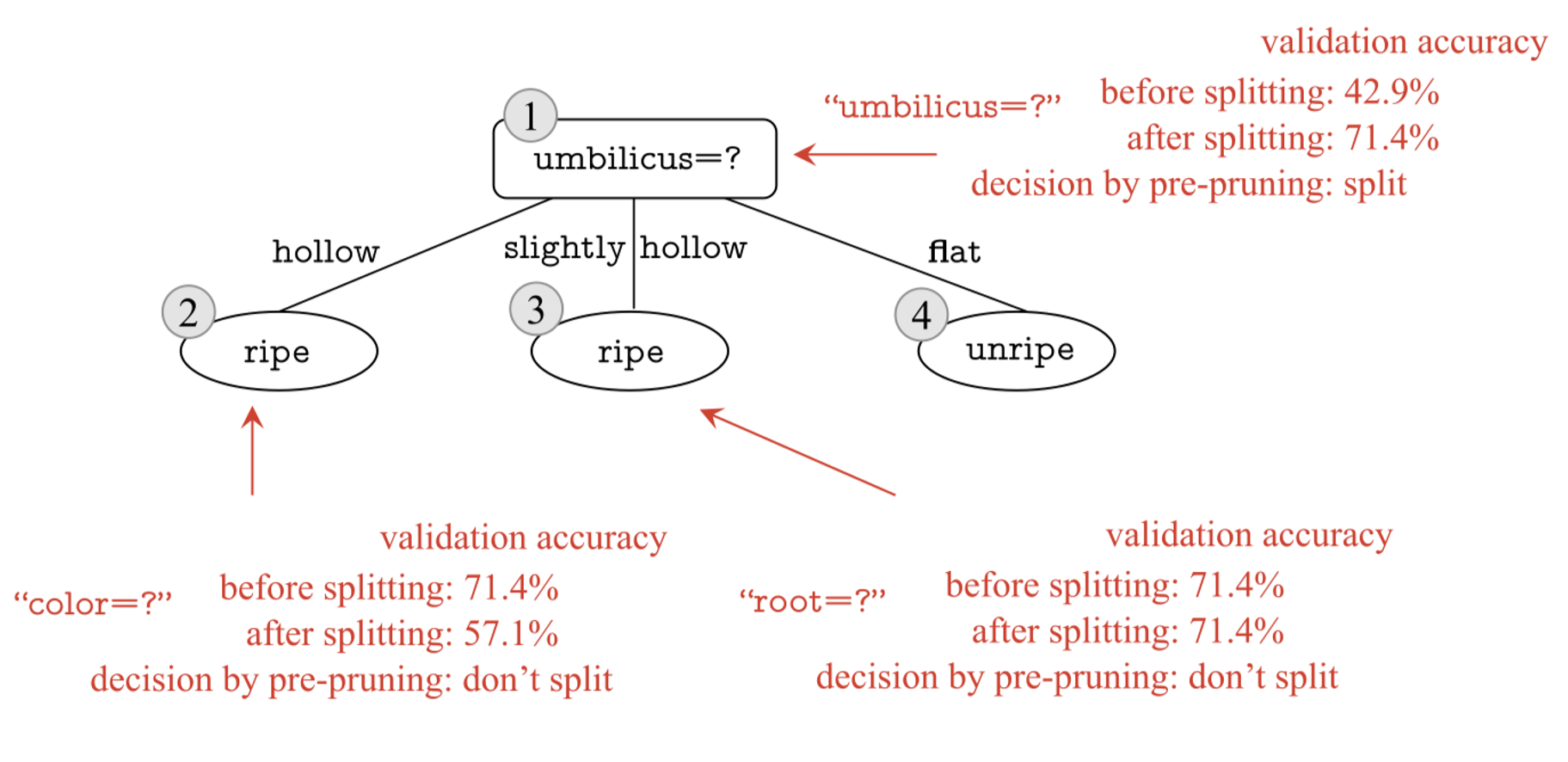
预剪枝的具体优缺点

优势（Advantages）：

减少过拟合：
- 通过提前停止树的分裂，限制决策树的复杂度，防止其过于拟合训练数据中的噪声。
减少计算开销：
- 预剪枝在生成过程中就提前停止分裂，减少了决策树构建的时间和测试阶段的计算开销。

劣势（Shortcomings）：

欠拟合的风险：
- 由于预剪枝过于“贪心”（Greedy），可能过早停止分裂，导致一些有价值的特征未被利用。
- 后续分裂虽然无法立即提高当前验证集性能，但可能对整体性能有正向影响。
过于依赖验证集：
- 验证集的表现受数据分布和样本量影响，如果验证集数据不足或不均匀，预剪枝效果可能不佳。

Post-pruning

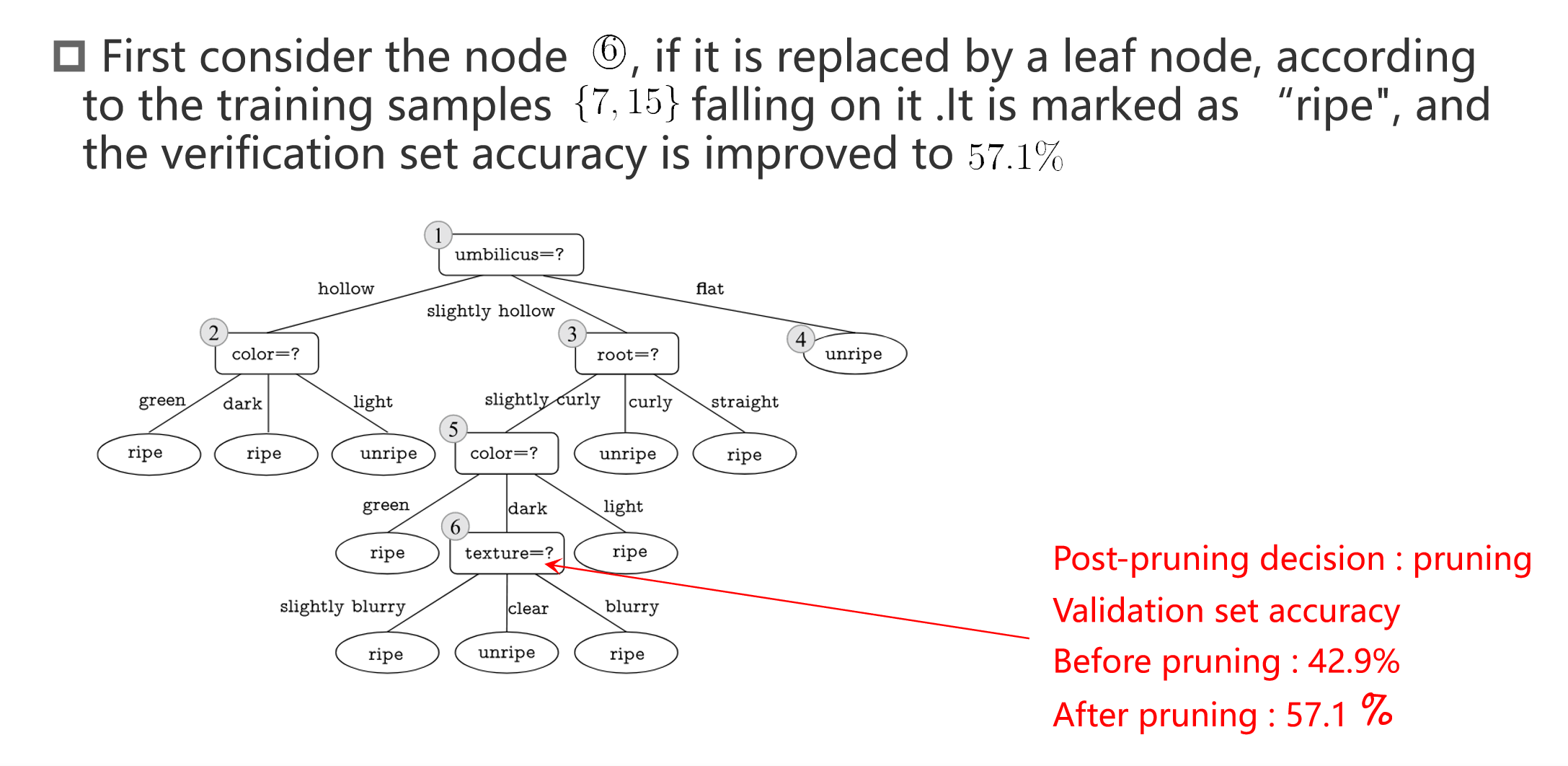
如果剪能够提高验证集分类的正确率，就 pruning。反之若不能就不剪。

后剪枝的优缺点

优点：保留更多分支，减少欠拟合风险，泛化性能较好。
缺点：训练时间较长，需要从下到上逐步检查所有非叶子节点。

Continuous and Missing Values

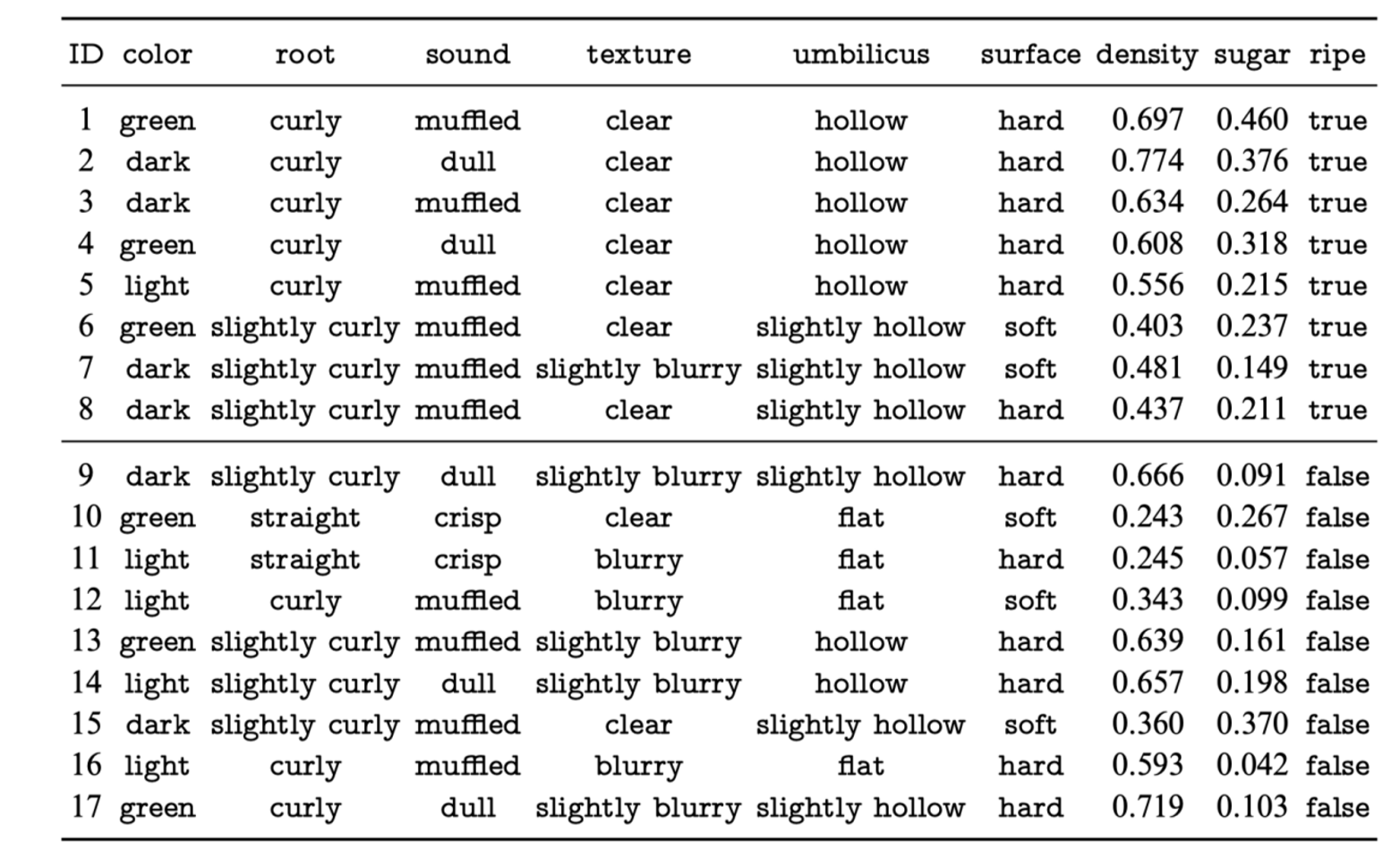
数据说明：包含连续特征（surface density 和 sugar）和分类特征。目标变量为 ripe（是否成熟）。

处理方式：

连续特征：
- surface density 和 sugar 是连续特征，通常需要进行分箱（Binning）或者标准化处理（Normalization）。
- 可以通过设定阈值将连续特征转换为离散值，比如“高”、“低”。
标签（目标值）：
- ripe 作为分类标签（布尔值）不需要特殊处理

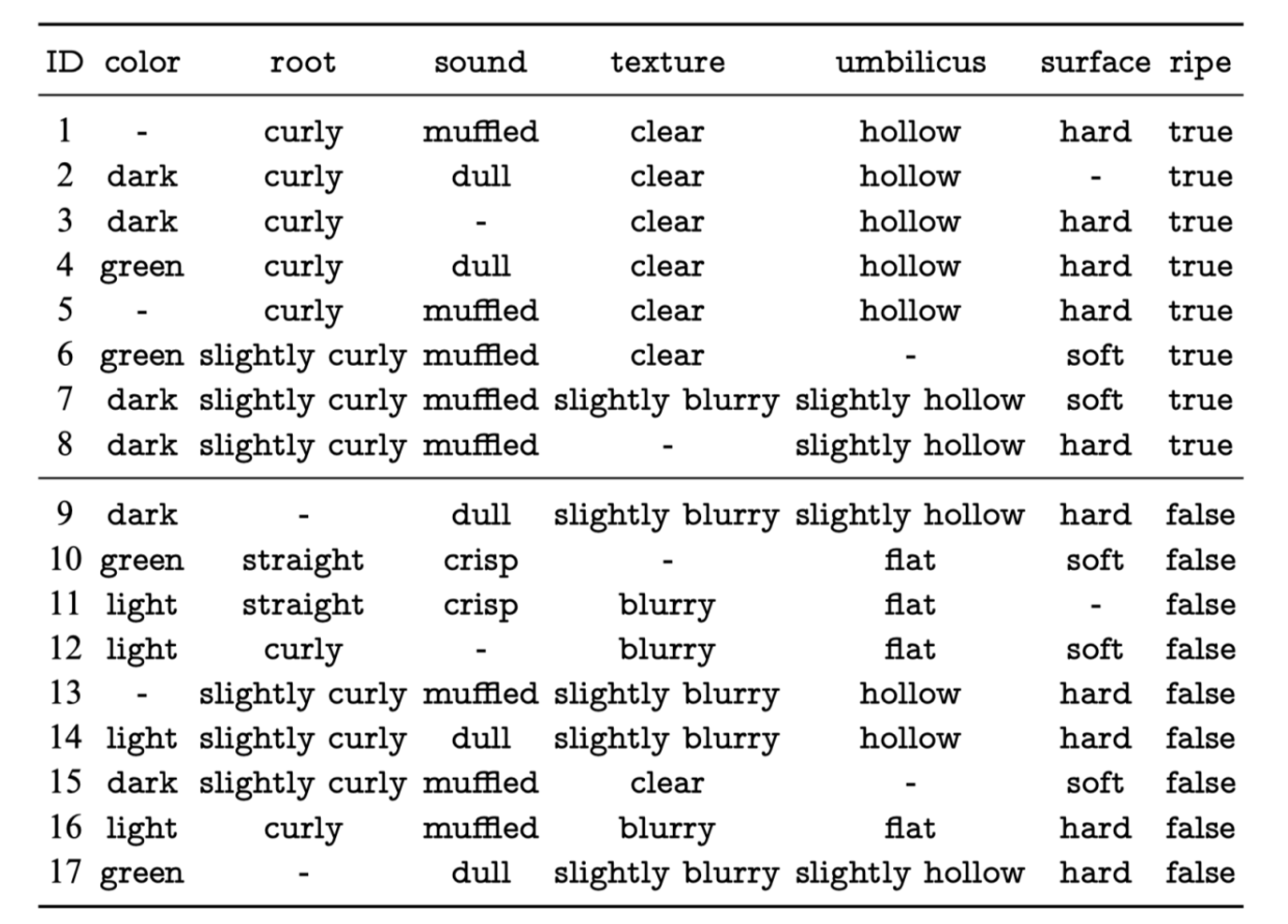
缺失值处理方法：

删除缺失值：如果缺失值比例较小，可以直接删除含缺失值的行或列。
填充缺失值：
- 数值型特征：用均值、中位数或众数填充缺失值。
- 分类型特征：用众数（最频繁出现的类别）或添加新类别（如 missing）填充。
预测缺失值：使用机器学习模型（如 KNN 或回归）预测缺失值。
标记缺失：添加二元特征标记缺失情况，帮助模型学习缺失值的影响。

Multivariate Decision Trees

下图清晰的展示了多变量决策树的优势：

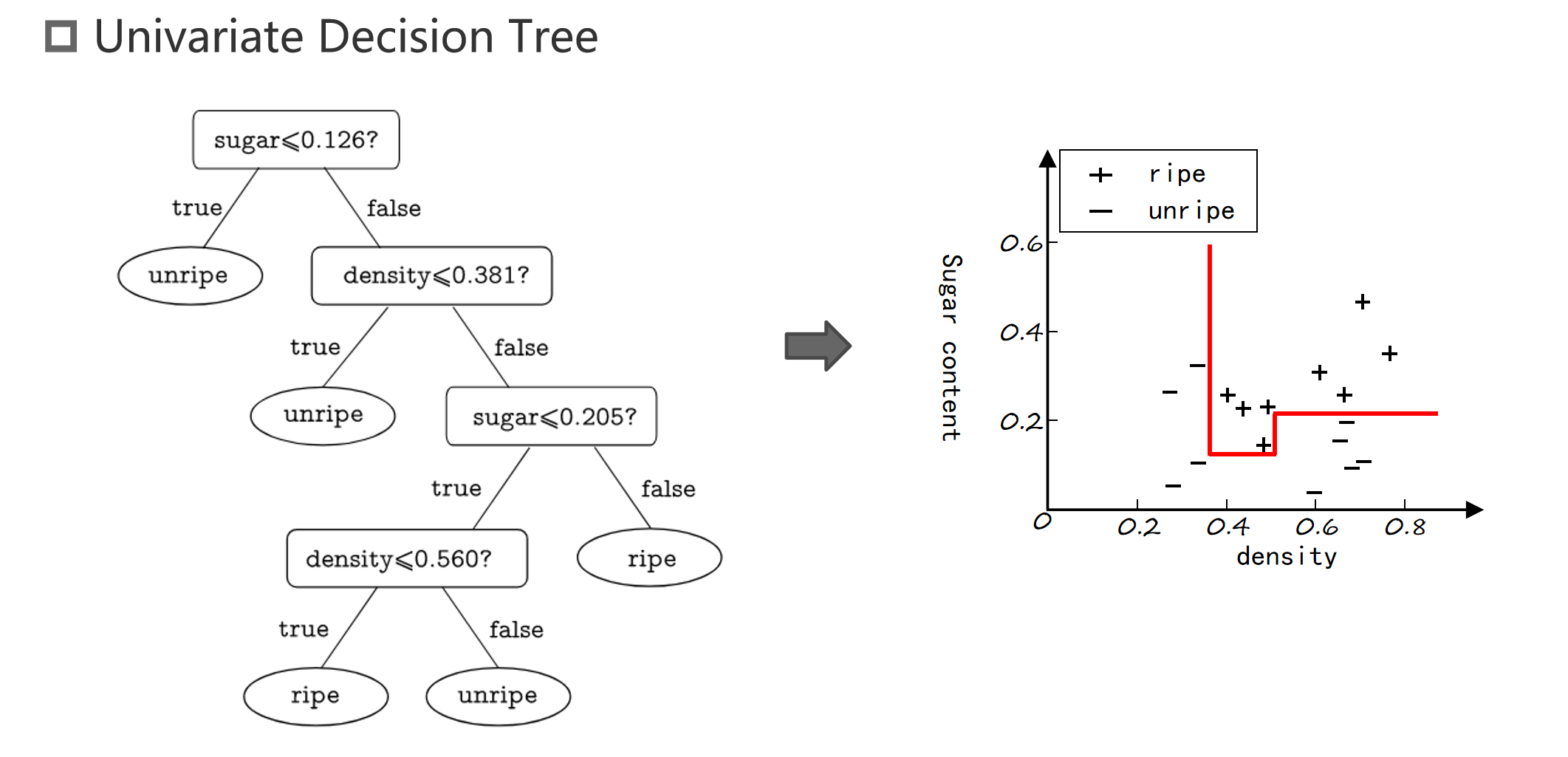
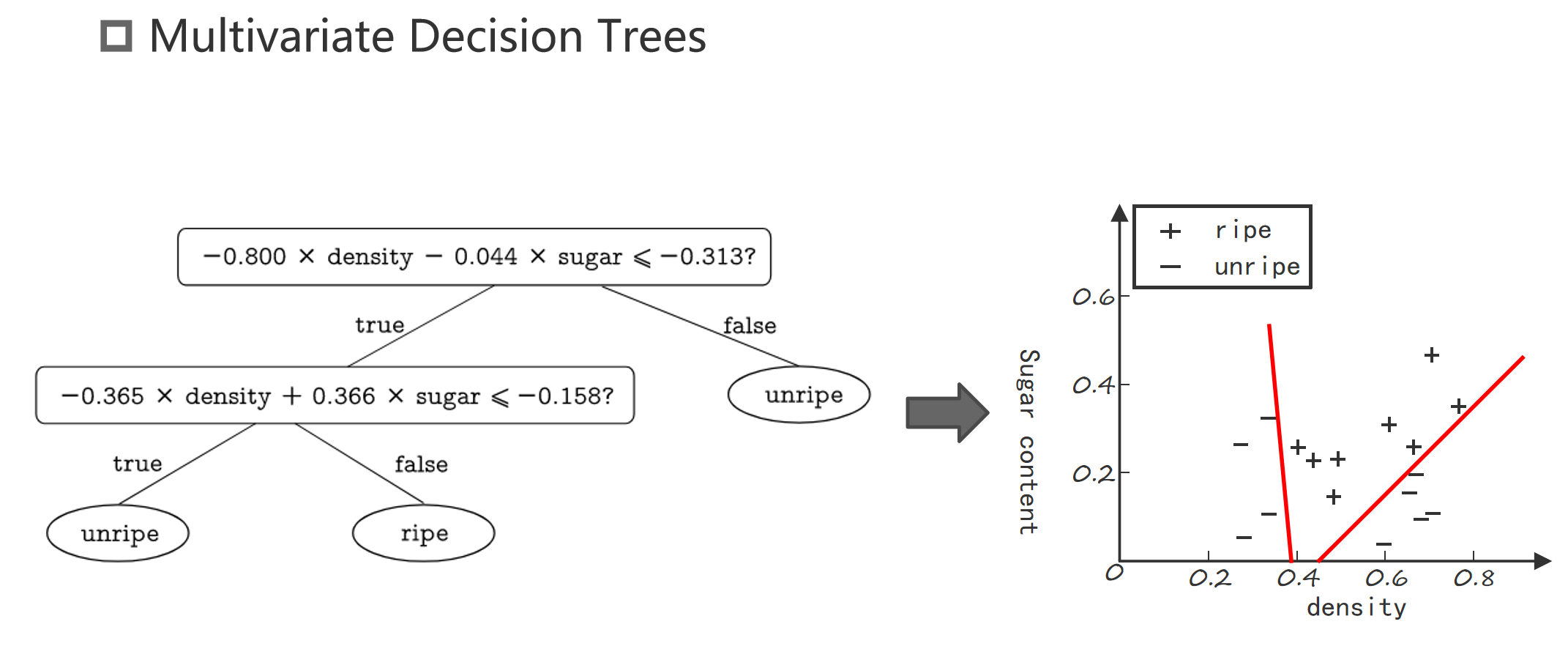
图例

总体

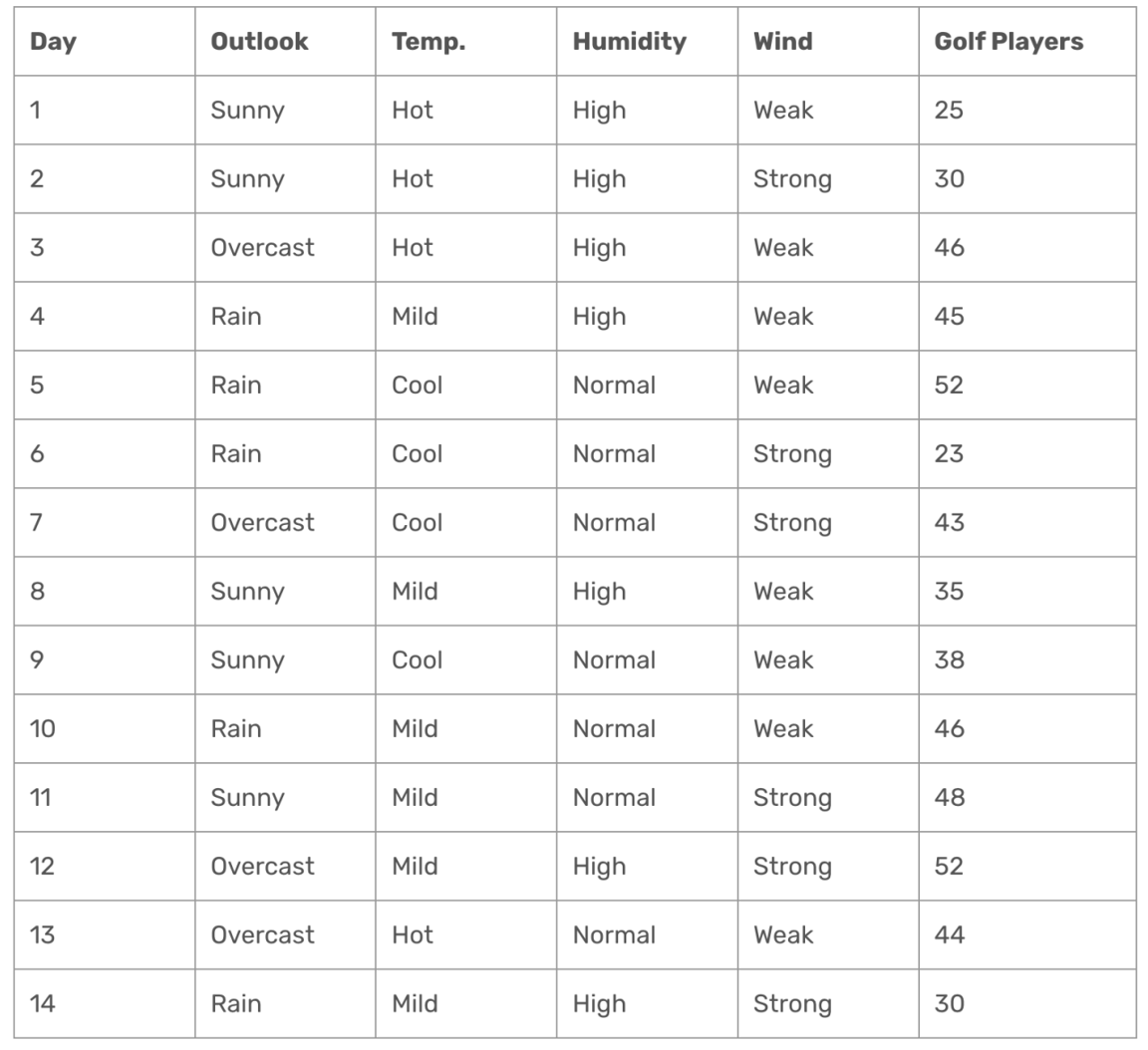
目标：使用 Outlook、Temp.、Humidity 和 Wind 预测 Golf Players（高尔夫球员人数）。

过程：

初始数据集的平均值 = 39.78。
初始数据集的标准差 = 9.32。
通过分裂特征，逐步减少标准差，找到最佳划分节点。

分组条件：Outlook = Sunny。

统计结果：

平均值 = 35.2：Sunny 分组的预测值。
标准差 = 7.78：表示数据波动性。

解释：

将 Outlook = Sunny 单独分为一组，标准差从整体的 9.32 降到 7.78，误差减小。
分裂后的预测结果更加准确，因为组内数据更集中。

Outlook = Overcast。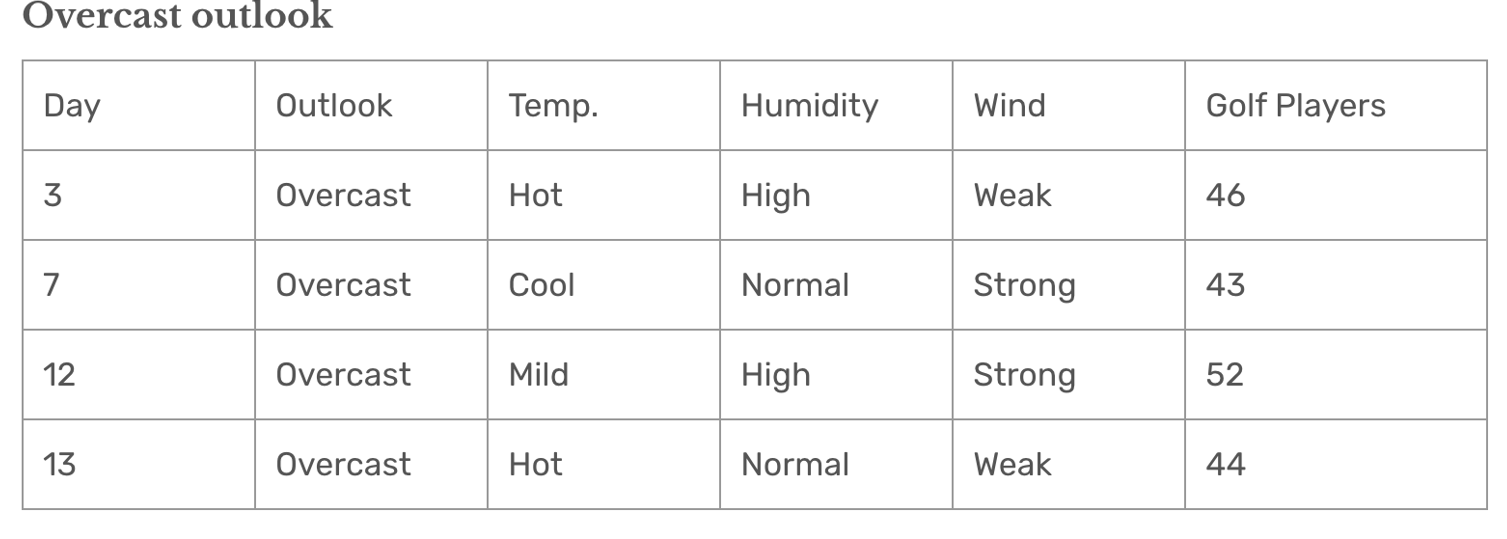

统计结果：

平均值 = 46.25：Overcast 分组的预测值。
标准差 = 3.49：比 Sunny 组的标准差（7.78）更小。

解释：

Overcast 组的数据更加集中，标准差最小，说明这一组的预测误差最低。
对于 Outlook = Overcast 的天数，使用平均值 46.25 进行预测是合理的。

Outlook = Rain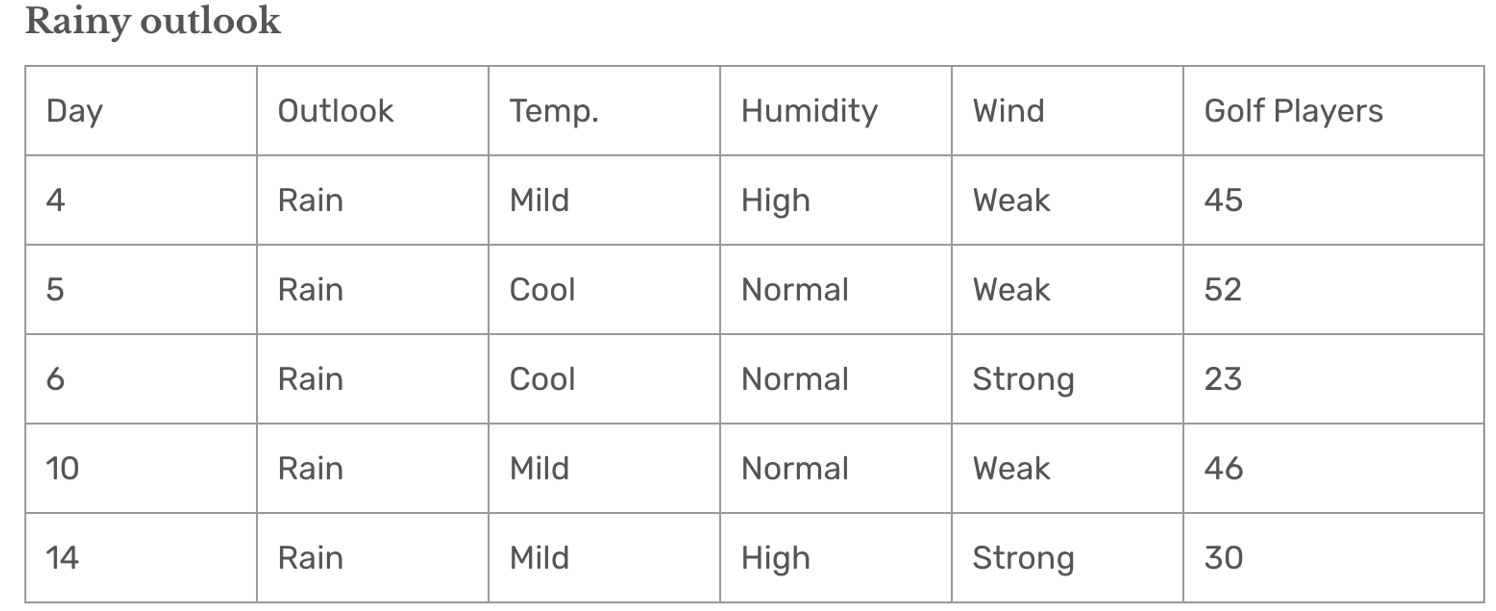

统计计算：

平均值 = 39.2。
标准差 = 10.87。

解释：

Rain 分组的标准差较大（10.87），说明数据分布较为分散，预测误差相对较高。

总结

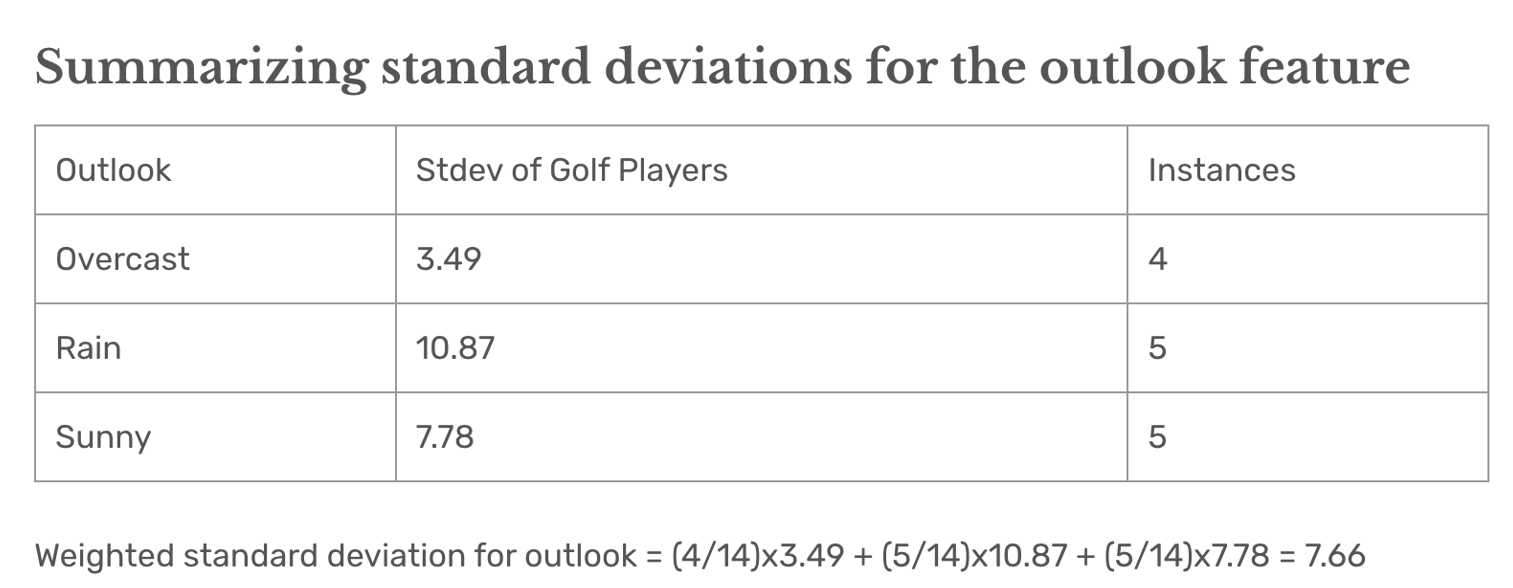
方差总共下降了 1.66，在回归树中，标准差减少量越大，说明分裂带来的数据纯度提升越高。因此，Outlook 特征被选为最佳分裂特征。

sum

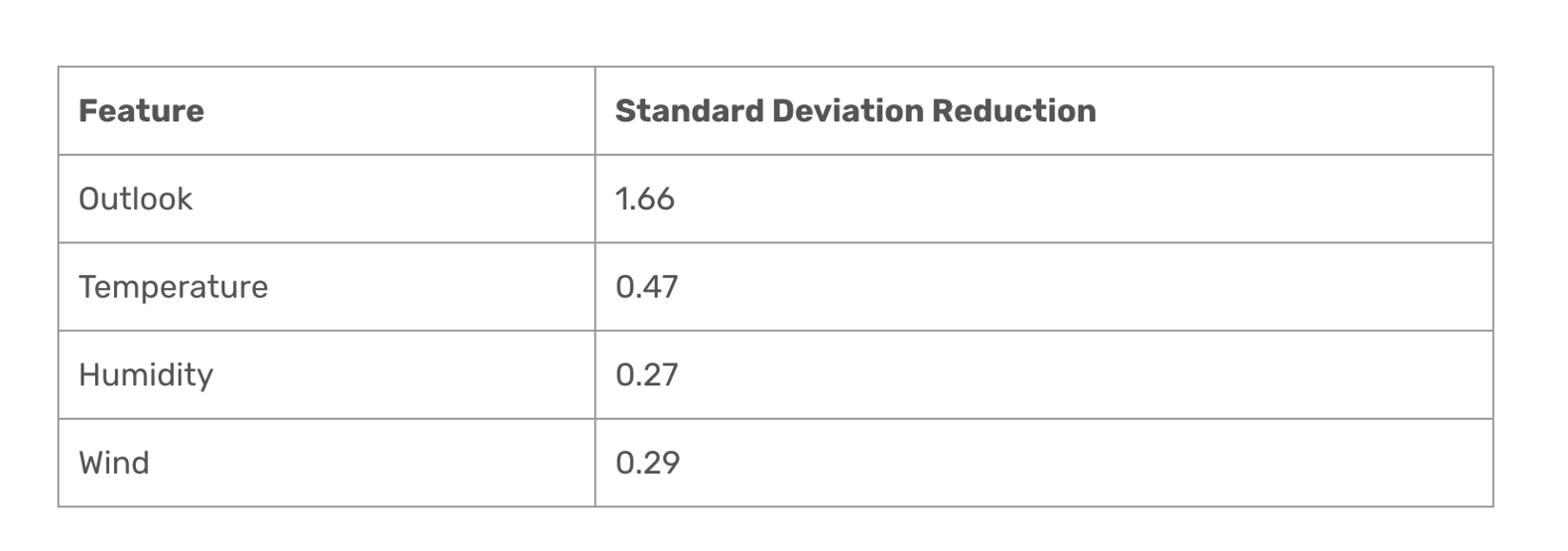
这是所有特征分类后方差下降的量。可以看到 outlook 是下降最多的，所以选择 outlook 特征分类：

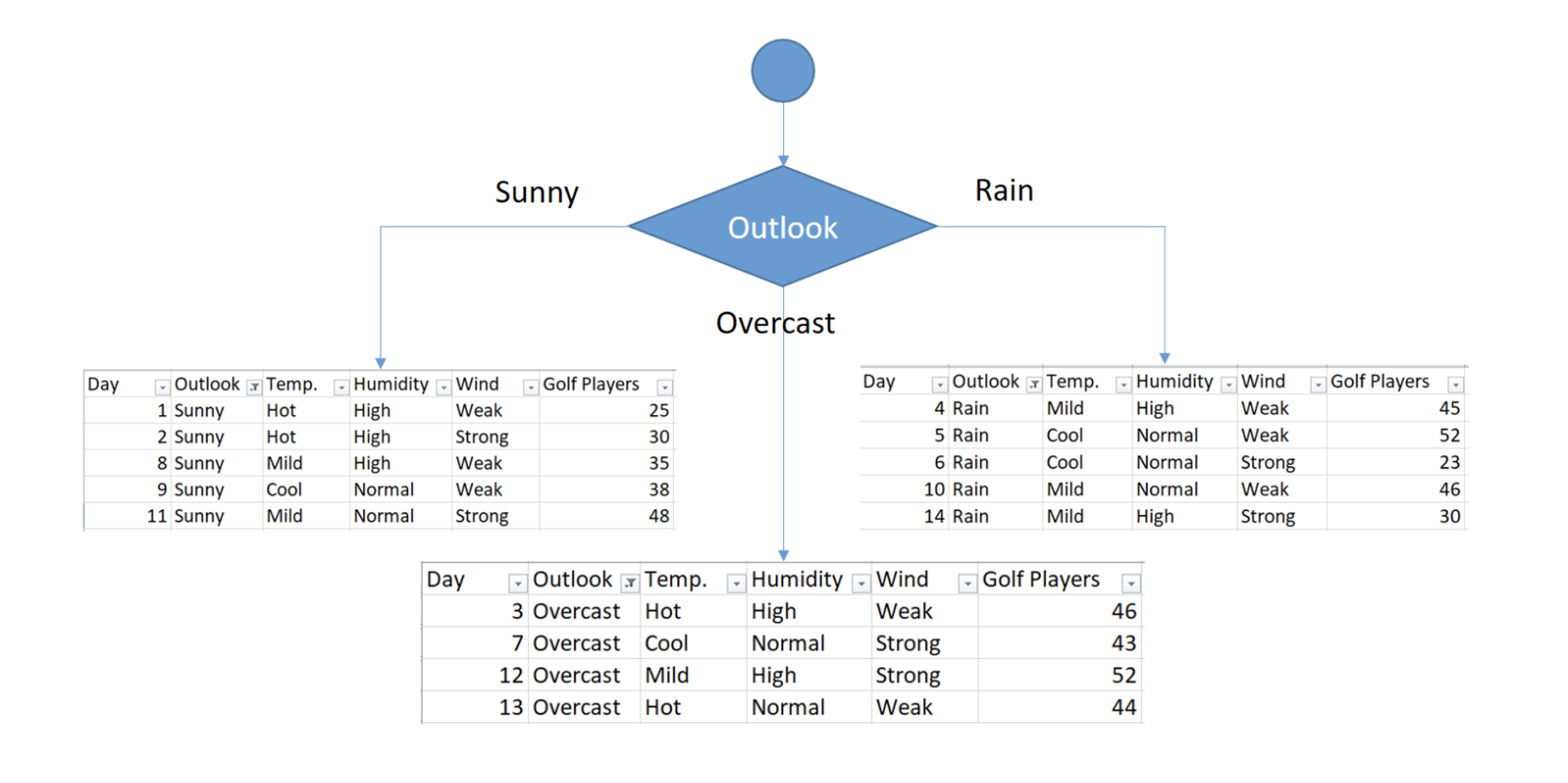
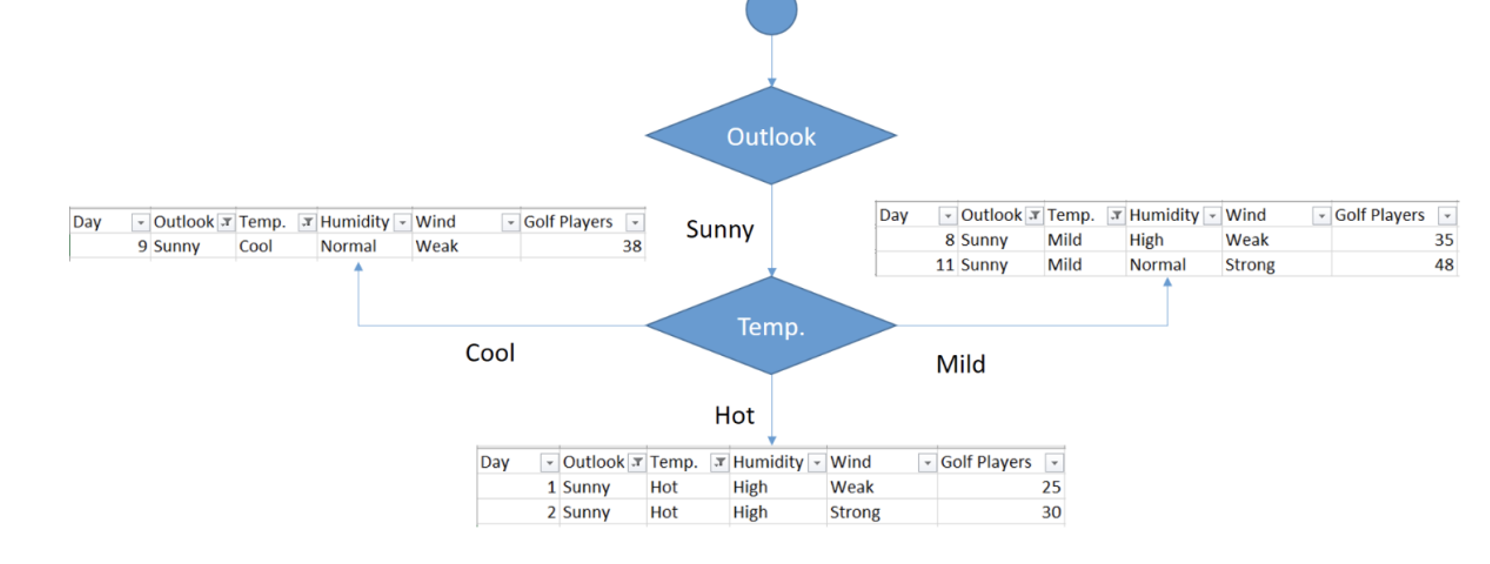
进一步分裂

1. Sunny Outlook 和 Temperature 分组分析

在 Sunny 分组下，根据 Temperature 特征将数据进一步细分：

（1）Sunny + Hot Temperature

Day	Temp.	Humidity	Wind	Golf Players
1	Hot	High	Weak	25
2	Hot	High	Strong	30

标准差：2.5
数据较集中，波动较小。

（2）Sunny + Cool Temperature

Day	Temp.	Humidity	Wind	Golf Players
9	Cool	Normal	Weak	38

标准差：0
只有一条数据，标准差为 0，代表数据完全集中。

（3）Sunny + Mild Temperature

Day	Temp.	Humidity	Wind	Golf Players
8	Mild	High	Weak	35
11	Mild	Normal	Strong	48

标准差：6.5
数据波动较大。

2. Sunny 分组下 Temperature 特征的加权标准差

通过加权平均计算 Sunny 分组下的 Temperature 标准差：

$Weighted Stdev = (\frac{2}{5} \times 2.5) + (\frac{1}{5} \times 0) + (\frac{2}{5} \times 6.5) = 3.6$

解释：温度特征将 Sunny 分组进一步划分后，整体加权标准差降到 3.6。

3. 标准差减少量

原始 Sunny 分组的标准差为 7.78。分裂后：

$标准差减少 = 7.78 - 3.6 = 4.18$

4. 其他特征的标准差减少量

特征	标准差减少量
Temperature	4.18
Humidity	3.33
Wind	0.85

结论：
- Temperature 特征的标准差减少量最大（4.18），因此被选为 Sunny 分组下的最佳分裂特征。

最后

1. Overcast 分组

数据：
Day Outlook Temp. Humidity Wind Golf Players
3 Overcast Hot High Weak 46
7 Overcast Cool Normal Strong 43
12 Overcast Mild High Strong 52
13 Overcast Hot Normal Weak 44
平均值：
$Average = \frac{46 + 43 + 52 + 44}{4} = 46.25$
标准差：标准差较小（3.49，见前面计算），表示数据非常集中，进一步分裂的必要性较低。

Day	Outlook	Temp.	Humidity	Wind	Golf Players
3	Overcast	Hot	High	Weak	46
7	Overcast	Cool	Normal	Strong	43
12	Overcast	Mild	High	Strong	52
13	Overcast	Hot	Normal	Weak	44

2. Rainy Outlook 分组

数据：
Day Temp. Humidity Wind Golf Players
4 Mild High Weak 45
5 Cool Normal Weak 52
6 Cool Normal Strong 23
10 Mild Normal Weak 46
14 Mild High Strong 30
最佳分裂特征：Wind
- 标准差减少量：7.62（最大）。
分裂结果：
- Weak 风力：平均值 = 47.7（包含较大值 45、52、46）。
- Strong 风力：平均值 = 26.5（包含较小值 23 和 30）。

Day	Temp.	Humidity	Wind	Golf Players
4	Mild	High	Weak	45
5	Cool	Normal	Weak	52
6	Cool	Normal	Strong	23
10	Mild	Normal	Weak	46
14	Mild	High	Strong	30

3. Sunny Outlook 分组

分裂特征：Temperature
分裂结果：
Temp. Golf Players 平均值
Cool 38
Hot 27.5
Mild 41.5
标准差减少量：4.18，效果显著。