所有知识点总结
week 02
Bogosort
时间复杂度:最坏情况是 O(n! * n),预期情况是 O(n!)。
【平均情况下,需要尝试 n! 次打乱才能生成一个正确排序。每次尝试包括:调用
is_sorted:复杂度为 O(n)。调用shuffle:复杂度为 O(n)。每次尝试的复杂度为 O(n+n)=O(n)】
空间复杂度:O(1),因为该算法是原地排序。代码见课件
Insertion Sort
时间复杂度:最优情况:O(n) 最坏情况:O(n²) 平均情况:O(n²) 空间复杂度:O(1) 对于小数据算法友好。 代码见课件
bubble sort
时间复杂度:最优情况:O(n) 最坏情况:O(n²) 平均情况:O(n²)
空间复杂度:O(1) 不太高效的一个排序方法。实现简单,但一般实际不会选择。

Quick Sort
时间复杂度: 最优情况:O(n log n) 最坏情况:O(n²) 平均情况:O(n log n)
最差情况发生在列表本身已经有序(升序或降序),选定的基准值总是列表中的最小值或最大值。此时,每次分区都会导致一个子列表为空,另一个子列表包含剩余的所有元素。递归深度为 n,每层分区的时间复杂度为 O(n)
空间复杂度:O(log n)(递归栈深度)最差情况下,是 O(n)
适合大规模数据排序。实际中基本是首选。虽然在最坏情况下时间复杂度可能退化为 O(n²),但通过选择合适的基准元素,可以避免最坏情况,通常其表现会非常优秀。
**pivot 值的选择:**如果数组数据完全随机并且数据较少,选择第一个或最后一个元素作为基准元素是简单且足够的。如果数组已经有部分排序并且数据较多,选择中值(最大值加最小值除以2)作为基准元素可以提高效率,避免最坏情况。中间值策略能更有效地分割数组,减少递归的深度,因此在大多数情况下,它能提升快速排序的性能
Merge sort
时间复杂度:最优情况:O(n log n) 最坏情况:O(n log n) 平均情况:O(n log n) 空间复杂度:O(n)

归并排序是一种 稳定 排序算法,它的时间复杂度稳定在 O(n log n),在处理大规模数据时效率较高。然而,由于它需要额外的空间来存储临时数组,因此它的空间复杂度为 O(n),这在某些内存有限的环境中可能是一个缺点。尽管如此,归并排序仍然是一个非常可靠和常用的排序算法,尤其在数据量大或数据需要稳定排序的场合。
每次合并时,需要遍历两个子数组的所有元素。对于大小为 n 的数组,合并每一层的总时间为 O(n)(因为每个元素只会被访问一次)。由于合并操作在每一层都进行,总共有 log2(n) 层,因此合并过程的时间复杂度为: O(n⋅logn)
分解的总复杂度为 O(logn)(递归树的高度)。合并的总复杂度为 O(n⋅logn)。因此,合并排序的总时间复杂度是: O(n⋅logn)
week 03
Binary Search
只能在排序好[sorted]的数据里查询。
时间复杂度:最优情况:O(1) 最坏情况:O(log n) 平均情况:O(log n) 空间复杂度:O(1):迭代版本 O(n):递归版本

Interpolation search
查找的数据是排序[sorted]好的,(均匀[uniform distribution]地,就是元素之间的间隔相同)
最优时间复杂度:O(log log n)(数据均匀分布时,一次查找就过滤掉了 n 个元素,找到了给定元素)
最坏时间复杂度:O(n)(数据分布不均匀时,搜索了 n 次才找到)
平均时间复杂度:O(log n)(数据分布均匀时, 有点类似于二分查找了) 空间复杂度:O(1)

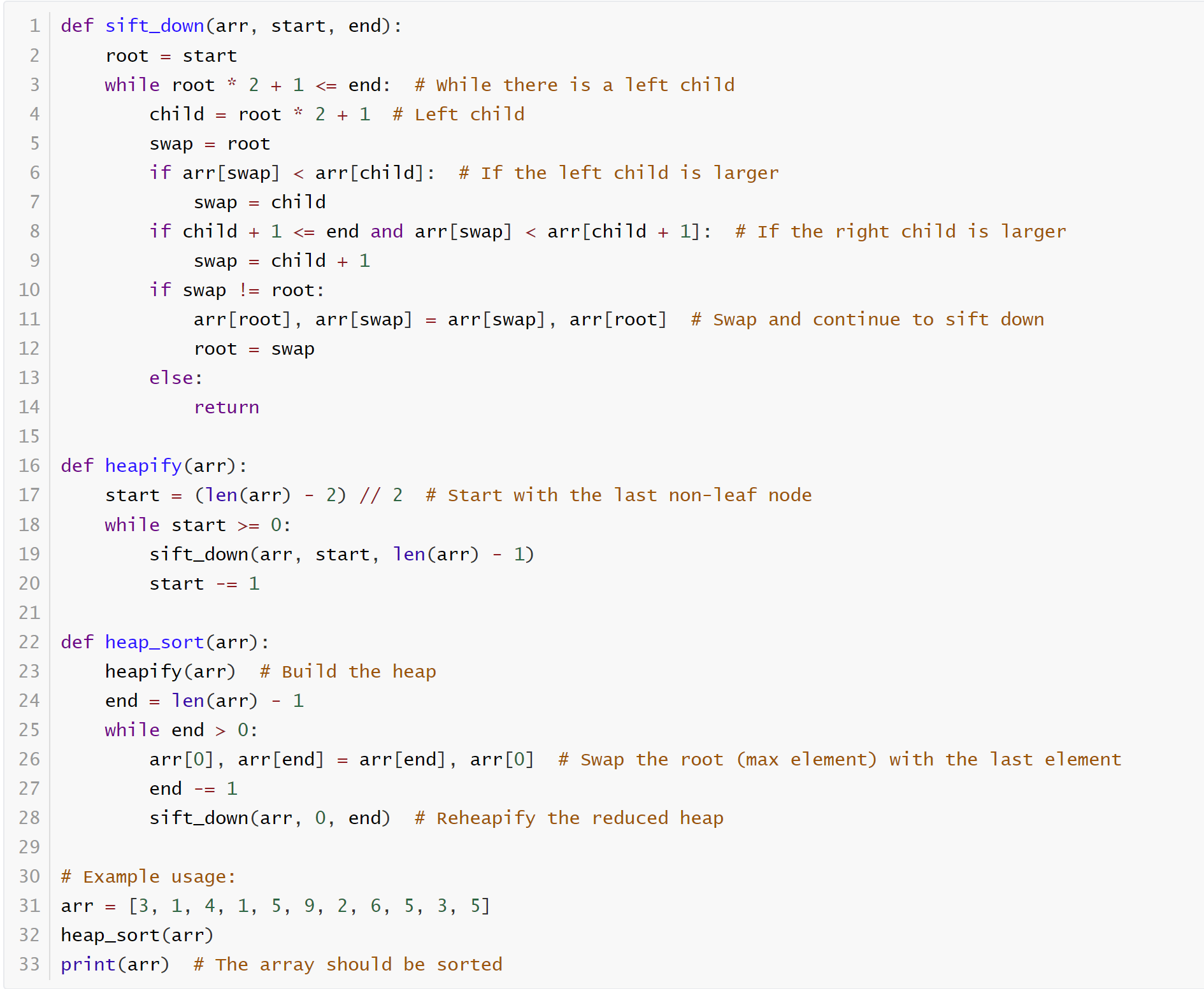
Heap sort
Arrangement of data as trees speeds up search by reducing the number of operations necessary to find a target
构建堆:构建最大堆或最小堆需要遍历堆的每一个节点,且调整每个节点的操作时间复杂度是O(log n)。因此,构建堆的时间复杂度是 O(n)。
堆排序:每次将根节点(最大值或最小值)与最后一个元素交换,然后调整堆的结构。每次调整的时间复杂度是 O(log n),共需要进行 n 次交换,因此堆排序的时间复杂度是 O(n log n)。一次 sift-down 的时间复杂度是
,因为树的深度是 ,最坏的情况一个节点要向下交换树的深度的次数。
综合起来,堆排序的总时间复杂度是 O(n log n)。 空间复杂度是 O(1)[迭代] O(logn)[递归]。
堆化后并不是排序好的列表,但是满足父节点永远大于其子节点,树扁平化的列表也遵循这个规则。Heapify 完了我们还需要 Sort。Sort完了是一个递增的列表。
Use recursive heap sort for small datasets. Use iterative heap sort for large datasets to avoid stack overflow.

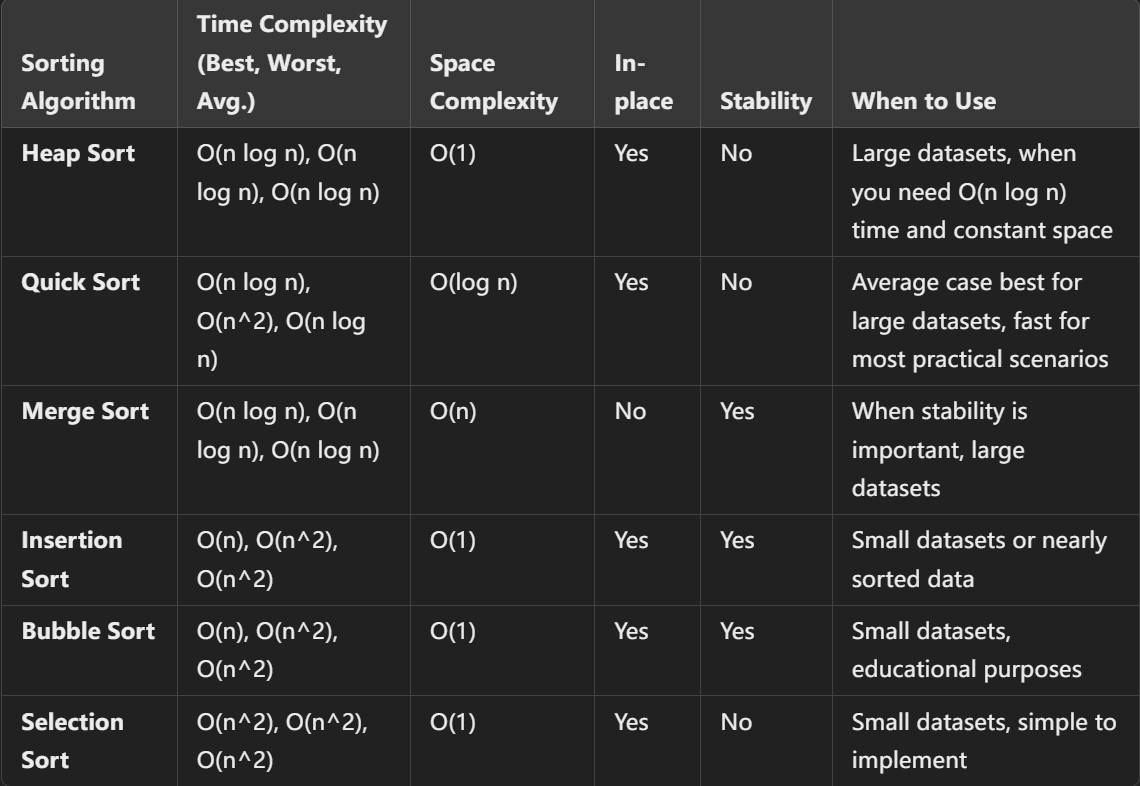
Heap Sort的主要优点是时间复杂度稳定为 O(n log n),即使在最坏情况下也是如此,适合处理大规模数据。缺点是其不稳定,并且在实际中比快速排序稍慢。在实际应用中,如果需要保证最坏情况的时间复杂度,堆排序是一个不错的选择;但如果数据规模适中且关注平均性能,快速排序通常会表现得更好因为快速排序只需要少量额外空间。快速排序 是较为高效的选择,特别是当数据集较小或数据接近随机分布时。但在处理非常大的数据集、要求稳定排序或对最坏情况性能要求较高时,合并排序 是一个更好的选择。
week 04
BSTs allow powerful, efficient search
在一个完全平衡的二叉树中,树的高度是 log n(n 是节点的数量),因此我们每向下遍历一层,就进行一次比较。所以在每一层都只需要做一次比较,而比较的层数和树的高度成正比。树的高度不受节点数量的影响,而是与树的结构(平衡)直接相关。 随着树越来越大,搜索所需要的比较次数相对于树的总节点数的比例越来越小。
Traversal
DFS —— search for unbalanced trees
BFS —— search for balanced trees

AVL
Insert (标红!!!)


delete
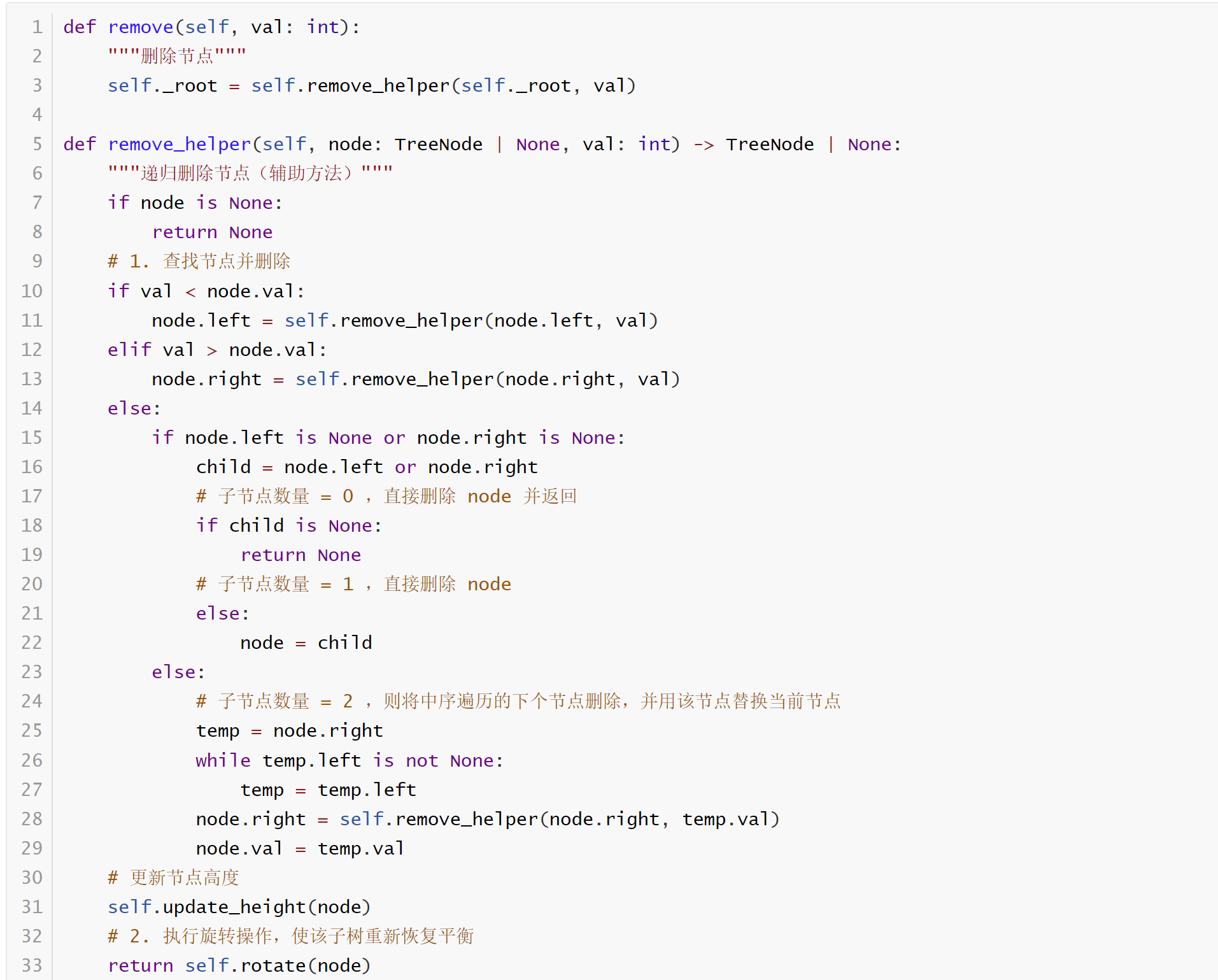
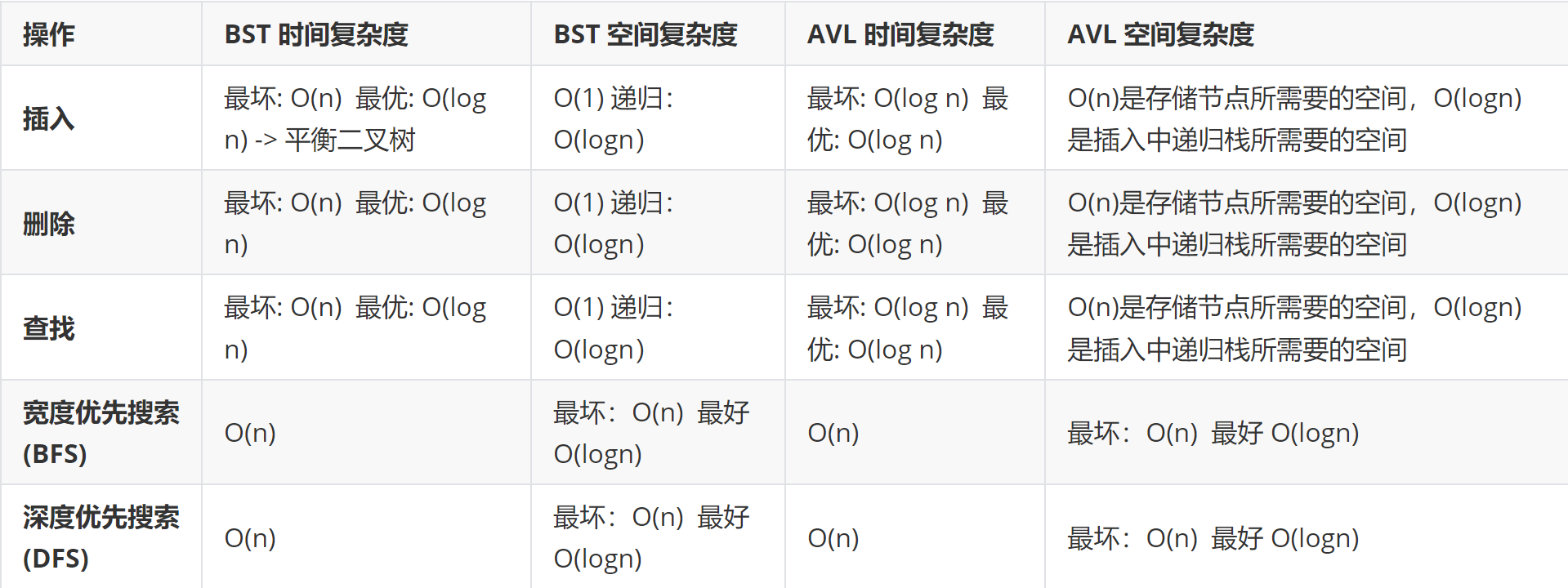
week 05
Hashing



Link list

Queue

Graph
DFS : 时间复杂度:O(V + E) 空间复杂度:O(V)

BFS : 时间复杂度:O(V + E) 空间复杂度:O(V)

week 06
Dijkstra’s algorithm : 时间复杂度:
寻找距离最小的节点:
min()函数的复杂度是 O(V),因为需要遍历所有未处理的节点Q。最多需要执行 V 次,因为每个节点都会被处理一次。
更新邻居的距离:O(E)
- 遍历每个节点的邻居对应图中的所有边,因此所有边的更新操作总计为 O(E)。每一次遍历一个节点都只遍历与它相连的边,而非所有边。遍历完所有节点后,所有边才被遍历了一遍。

如果用最小堆实现,时间复杂度:distances 字典和优先队列都占用 O(V) 的空间。
弹出最小元素的操作:每个节点最多被弹出一次,时间复杂度是 O(V log V)。更新邻接节点的操作:每条边都会被遍历并插入到优先队列中,时间复杂度是 O(E log V),其中
E是图中的边数。
Prim’s algorithm : 时间复杂度:O(V * E)
外层循环执行 V-1 次,每次执行时内层循环遍历所有邻接边,最坏情况下每条边都会被遍历一次
空间复杂度:O(V + E)
图
graph存储了所有节点及其邻接边,空间复杂度为 O(V + E)。

kruskal’s algorithm: 时间复杂度:
在 Kruskal 算法中,首先需要将所有边按权重升序排列。这一操作的时间复杂度是 O(E log E),其中 E 是图中的边数
空间复杂度:


Dijkstra’s algorithm: Single Source Shortest Path Problem
Given: directed graph G = (V, E) in which each edge has a non negative label and one vertex is specified as the source.Determine the cost of the shortest path from the source to every other vertex in V
Prim’s algorithm: An MST aims to connect ALL the nodes in a graph at minimum cost.
MST 是否包含所有可能的最短路径? 不包含。MST 的目标是覆盖所有节点,且总权重最小,但它不能保证任意两个节点之间的路径是最短的。
Prim 是否让 Dijkstra 算法多余? 不会。Prim 算法的目标是生成 MST,而 Dijkstra 的目标是找到单源最短路径。两者解决的问题完全不同,互不替代
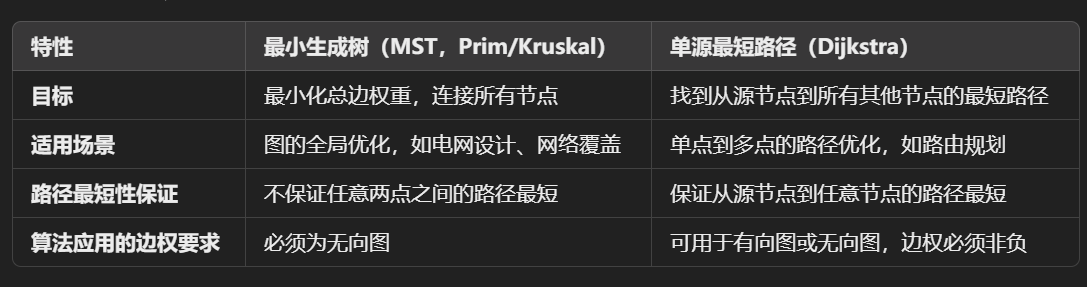
Kruskal’s algorithm:
Kruskal’s obviously avoids cycles. But how does Prim’s avoid cycles? : Prim avoids loops by connecting only new nodes and is naturally loop-free by design. Because it just chooses the lowest value unreached node; does not need to check for cycles. Cycles cannot happen in Prim’s as cycles involve already visited nodes…… and Prim’s will only consider unvisited nodes

Kruskal 算法通过对所有边进行排序,直接从排序后的边列表中按顺序选取最小的边,这避免了像 Prim 那样需要在当前的节点集合中搜索最小权值边。在稠密图中,边的数量接近
( 是节点数),排序所有边需要较高的时间成本。此外,Kruskal 算法还需要使用并查集频繁检测环路,稠密图中这一过程的开销会更大,降低效率。
week 07
When a greedy algorithm gives us an optimal solution, and why
最优子结构(Optimal Substructure): 定义:一个问题的解可以通过子问题的最优解合成,即每个子问题的最优解一定是整体问题的最优解的一部分。
无后效性(Greedy Choice Property): 定义:当前的贪婪选择不会影响后续的选择,也不会影响全局最优解的达成。
greedy algorithms can be optimal: this applies to Dijkstra. What about Prim / Kruskal?
都是最优的。前提是边是非负的。后俩需要图示联通的
When a greedy algorithm does not give us an optimal solution, and why
A greedy algorithm fails when the problem does not satisfy the "greedy-choice property" or the "optimal substructure". Specifically, the greedy algorithm's local optimal choices at each step may prevent it from achieving the global optimal solution.
为啥回溯对于最优解是必要的?
Backtracking explores all possibilities systematically, ensuring the optimal solution.But takes time to run.
week 08
NP-hard problems can exhibit different behaviours on different runs for the same input variables.
Heuristics
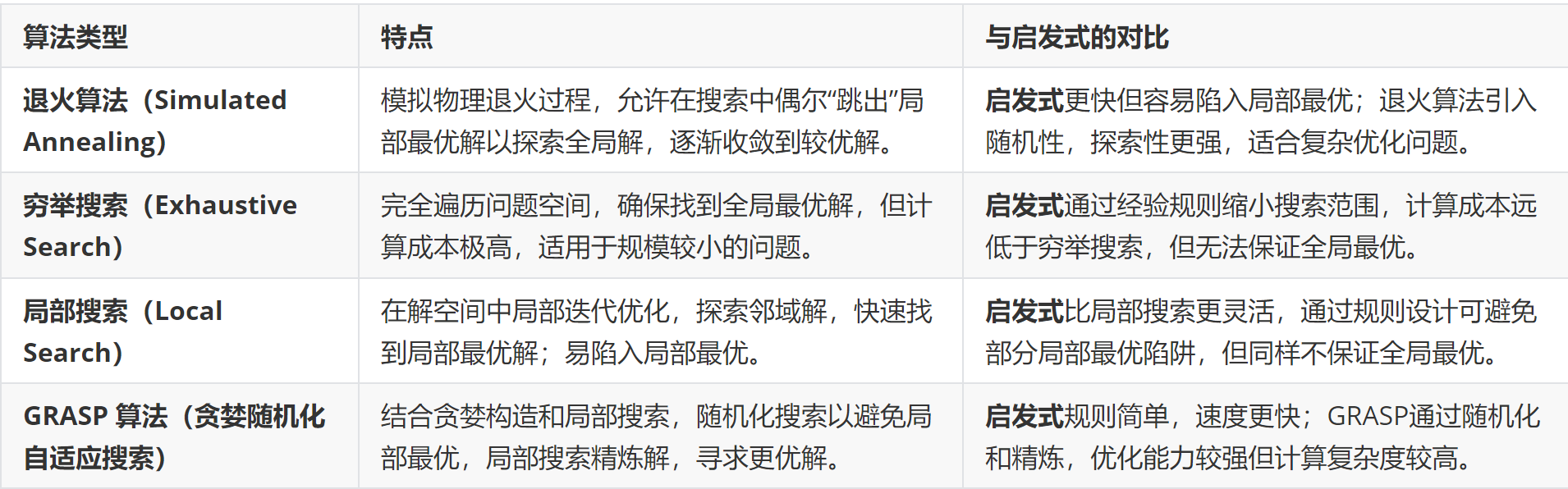

Local search

Simulated Annealing
退火算法的优点:能跳出局部最优。在温度较高时接受较差解,鼓励探索;在温度较低时专注于局部优化。
**怎么跳出局部最优解?**虽然初始解固定,但算法通过邻域搜索和随机接受较差解,可以有效探索更大范围的状态空间。

GRASP
GRASP 对退火算法的优化作用 :改进初始解的质量 增强解的多样性 减少退火算法的参数依赖性 提高全局最优解的搜索效率


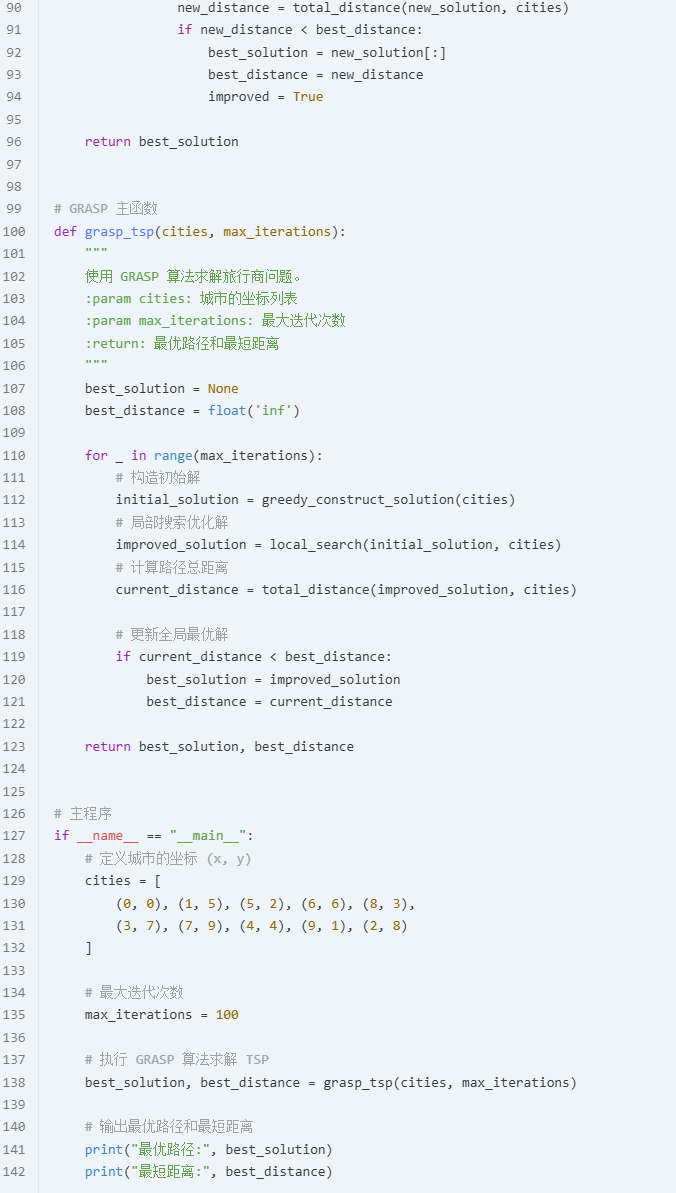
week 09
chat sever

data race
Thread 1 reads
my_var[0], gets1, and prepares to add1. 2. Thread 2 also readsmy_var[0], gets1, and prepares to add1. 3. Both threads compute the result2and write it back tomy_var[0].Result: Thread 2 started before Thread 1 finished. For instance,
my_var[0]only increases by1instead of2because both threads modify it simultaneously, causing one update to overwrite the other and resulting in a lost update. One element may have been incremented by2while its neighboring element may have only been incremented by1.
thread.setDaemon(True) # 可以把非守护线程设置为守护线程。不等待子线程结束主线程就会结束。多个线程是操作是公用内存的,即使放在线程池里也要加锁避免数据竞争。
lock
from concurrent.futures import ThreadPoolExecutor
from threading import Event, Lock
from time import time, sleep
# 初始化 Event 和 Lock
event = Event()
data_lock = Lock()
def modify_variable(var):
while True:
with data_lock:
for i in range(len(var)):
var[i] += 1
if event.is_set():
break
print('Stop printing')
# 要操作的共享变量
my_var = [1, 2, 3]
# 创建线程池
with ThreadPoolExecutor(max_workers=2) as executor:
# 提交任务到线程池
executor.submit(modify_variable, my_var)
executor.submit(modify_variable, my_var)
t0 = time()
while time() - t0 < 5:
try:
with data_lock:
print(my_var)
sleep(1)
except KeyboardInterrupt:
event.set()
break
# 设置 event 来停止线程
event.set()
# 打印最终结果
print(my_var)queue
from concurrent.futures import ThreadPoolExecutor
from threading import Event
from time import time, sleep
from queue import Queue
# 初始化 Event
event = Event()
def modify_variable(queue_in, queue_out):
while True:
if not queue_in.empty():
var = queue_in.get()
for i in range(len(var)):
var[i] += 1
queue_out.put(var)
if event.is_set():
break
print('Stop printing')
# 初始化变量和队列
my_var = [1, 2, 3]
queue1 = Queue()
queue1.put(my_var)
# 使用线程池
with ThreadPoolExecutor(max_workers=2) as executor:
executor.submit(modify_variable, queue1, queue1)
executor.submit(modify_variable, queue1, queue1)
t0 = time()
while time() - t0 < 5:
try:
print(my_var)
sleep(1)
except KeyboardInterrupt:
event.set()
break
# 设置事件以停止线程
event.set()
# 打印最终结果
if not queue1.empty():
print(queue1.get())week 10
什么时候需要用 await?有 I/O 操作的函数(如网络请求、文件读写)。需要等待的任务调度(如 asyncio.sleep)。依赖另一个异步任务的完成
IO & CPU
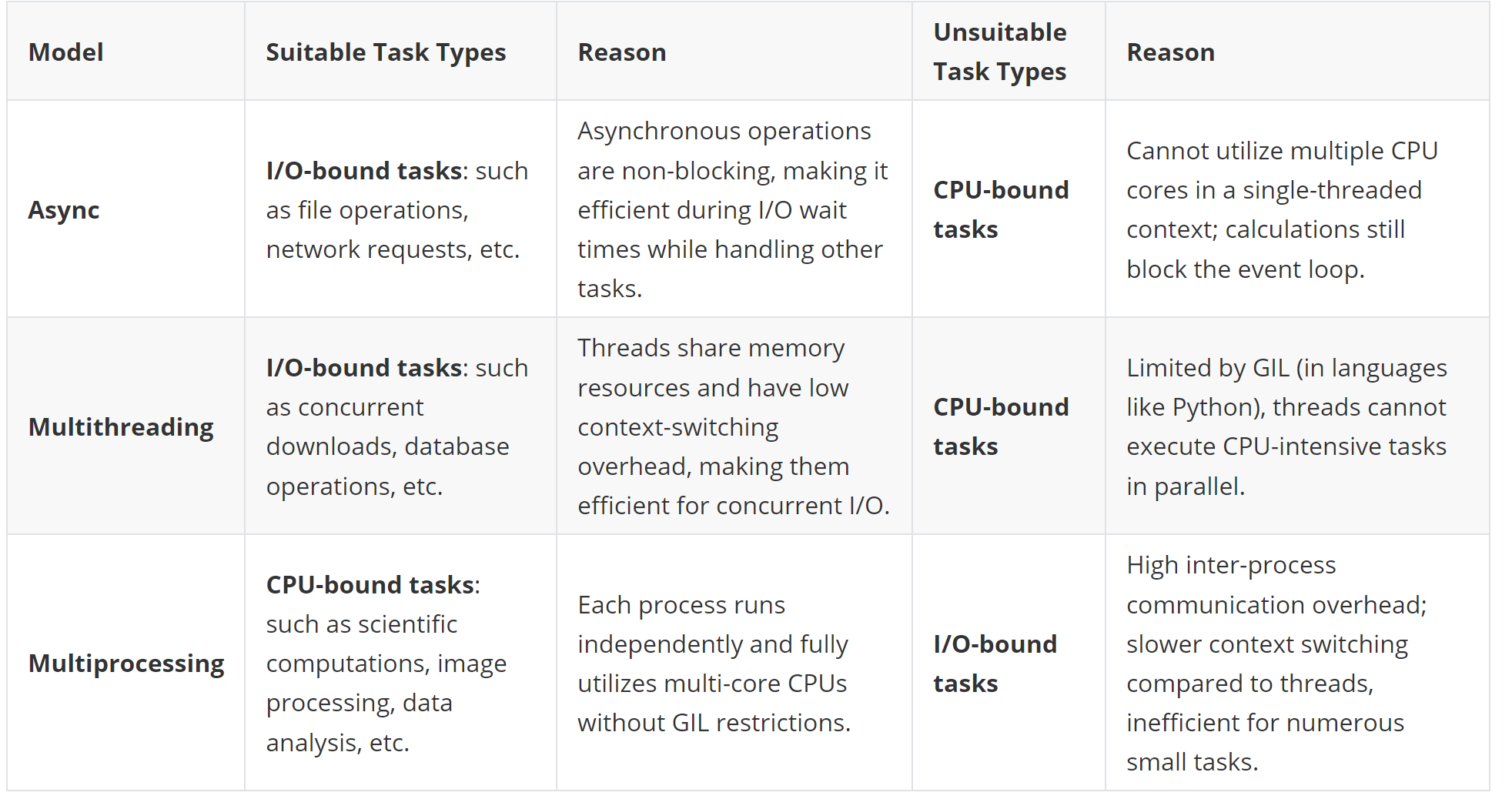
Async: Best for I/O-bound tasks, leveraging event-driven mechanisms to efficiently handle a large number of concurrent connections. Multithreading: Ideal for concurrent I/O-bound tasks that require shared resources but less suitable for CPU-intensive tasks due to GIL constraints.Multiprocessing: Optimal for CPU-bound tasks, offering independent execution and full multi-core utilization but less efficient for small, frequent task switches due to higher overhead.
chained_coroutines.py
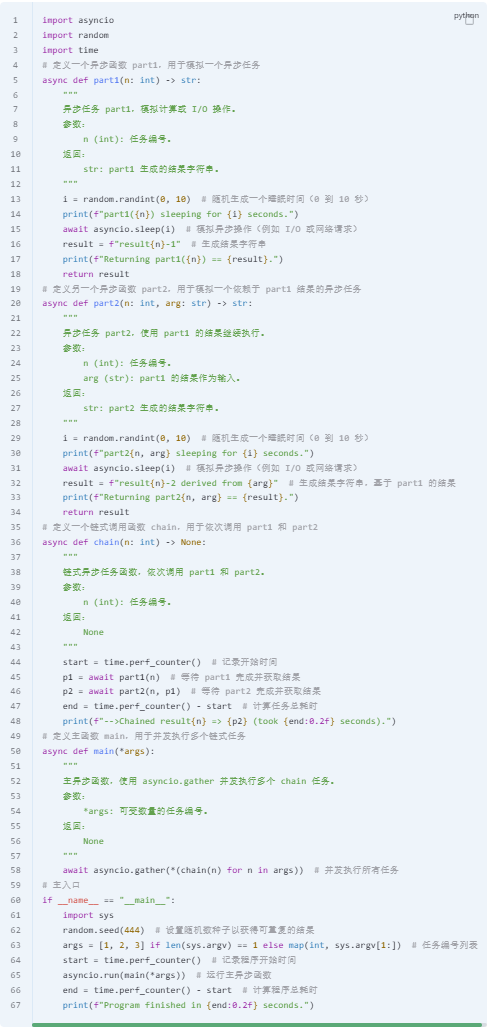
queue_producers_consumers.py

data_order.py

data_sharing queue

- 创建并发的
worker:
- 调用 ,同时启动了两个 协程。每个
worker会从队列中取出任务并执行,直到队列为空。
worker(queue)的执行:
worker循环运行:每次循环,调用queue.get()从队列中取出一个任务。执行 调用queue.task_done(),标记队列中的这个任务已完成。如果队列为空,worker循环结束。- 并发处理:因为有两个
worker,两个任务会并发运行,每个worker都在独立处理任务。当队列中有 3 个任务时,两个worker会同时取任务并运行,减少总处理时间。
- 任务完成与清理:
asyncio.gather()等待所有worker完成任务(即队列中的所有任务都被取出并处理)。当worker处理完所有任务,main()返回,asyncio.run()退出事件循环。
