高级算法——第6, 7周查漏补缺

Week 06

Dijkstra’s algorithm

手写过程

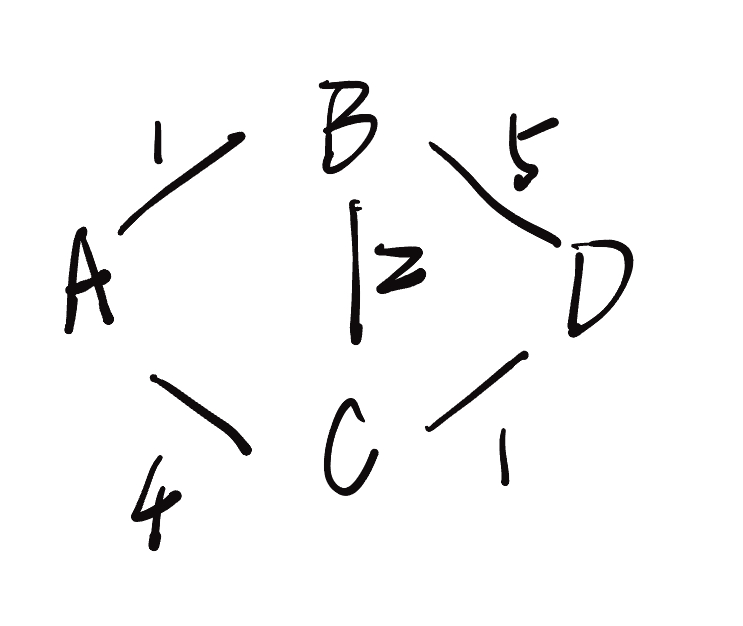
node	最开始	while 1开始时	while 2开始时	while 3开始时	while 4开始时	while 5开始时	while 6开始时
A	~	0	0	0	0	0	0
B	~	~	1	1	1	1	1
C	~	~	4	3	3	3	3
D	~	~	~	6	4	4	4

第一次 while：

1. 第一次 while 开始时：priority_queue:[(0,A)]

2. current_distance, currentg_node = 0, A, 弹出 (0, A)

3. 0 = distances[A], 循环继续

4. 遍历 graph[A]. neighbor:[B;C]; weight:[1,4]

5. 先 B。distance = 0 + 1，1 < ~，加入距离表。 (1, B)加入第一步那个队列

6. 再C。distance = 0 + 4，4 < ~，加入距离表。(4, C)加入第一步那个队列

第二次 while

1. priority_queue:[(1, B), (4, C)]

2. current_distance, currentg_node = 1, B，弹出 (1, B)

3. 1 = distance[B] = 1, 循环继续

4. 遍历 graph[B]. neighbor:[A,C,D],weight[1,2,5]

5. A. distance = 0 + 1, 1 > 0, 不加入距离表也不加入队列。

6. C. distance = 1 + 2, 3 < 4, 修改距离表，(3, C)加入队列

7. D.distance = 1 + 5, 6 < ~, 修改距离表，(6, D)加入队列

第三次 while

1. priority_queue:[(4,C),(3,C),(6,D)]

2. current_distance, current_node = 3, C, 弹出 (3, C)

3. 3 = distances[C] = 3, 循环继续

4. 遍历 neighbor = [A, B, D], weight = [4, 2, 1]

5. A. 跳过，类似上面

6. B。 distance = 3 + 2， 5 > 1跳过

7. D。 distance = 3 + 1，4 < 6，修改距离表，加入队列

第四次 while

1. priority_queue: [(4, D),(4,C),(6，D)]
2. 假设这里先弹出 C。current_distance, current_node = 4, C, 弹出 (4，C)
3. 4 > distances[C] = 3, 循环结束。

第五次 while

1. priority_queue: [(4, D),(6，D)]

2. current_distance, currentg_node = 4, D, 弹出 (4，D)

3. 4 = 4，循环继续

4. 遍历 neighbor = [B, C], weight = [1, 5]

5. B. distance = 4 + 1, 5 > 1跳过

6. C. distance = 4 + 5, 9>3跳过

第六次 while

1. priority_queue: [(6，D)]
2. current_distance, currentg_node = 6, D, 弹出 (6，D)
3. 6 > distances[D] = 4，循环结束。

priority_queue空了，跳出 while 循环。

代码

import heapq

def dijkstra(graph, start):
    distances = {node: float('inf') for node in graph}
    distances[start] = 0
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)
        if current_distance > distances[current_node]:
            continue
        for neighbor,weight in graph[current_node].items():
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances


graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}

# 从起点A运行 Dikjkatra 算法,计算到所有其他节点的最短路径
start_node = 'A'
shortest_path = dijkstra(graph, start_node)

# 输出从起点到其他所有结点的最短距离
print(f'从节点{start_node}到其他节点的最短距离为：')
for node, distance in shortest_path.items():
    print(f"{start_node}->{node}: {distance}")

def dijkstra(graph, origin, destination):
    # 初始化数据
    dist = {vertex: float('inf') for vertex in graph}  # 距离初始化为无穷大
    previous = {vertex: None for vertex in graph}  # 前置节点初始化为 None
    dist[origin] = 0  # 起点到起点的距离为 0
    Q = set(graph.keys())  # 所有节点加入集合

    while Q:
        # 找到 Q 中距离最小的节点
        u = min(Q, key=lambda vertex: dist[vertex])

        if dist[u] == float('inf'):
            break  # 如果最小距离是无穷大，说明没有到达目的地的路径

        if u == destination:
            break  # 到达目的地，停止循环

        Q.remove(u)  # 从 Q 中移除节点

        # 更新邻居节点的距离
        for neighbor, cost in graph[u].items():
            alt = dist[u] + cost  # 计算新的可能距离
            if alt < dist[neighbor]:  # 如果新的距离小于当前记录的距离
                dist[neighbor] = alt  # 更新距离
                previous[neighbor] = u  # 更新前置节点

    # 构造最短路径
    S = []
    u = destination
    while previous[u] is not None:
        S.insert(0, u)  # 插入路径
        u = previous[u]
    if u == origin:
        S.insert(0, u)  # 将起点加入路径
    return S


# 示例用法
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}

origin = 'A'
destination = 'D'
shortest_path = dijkstra(graph, origin, destination)
print("Shortest Path:", shortest_path)

Prim’s algorithm

手写过程

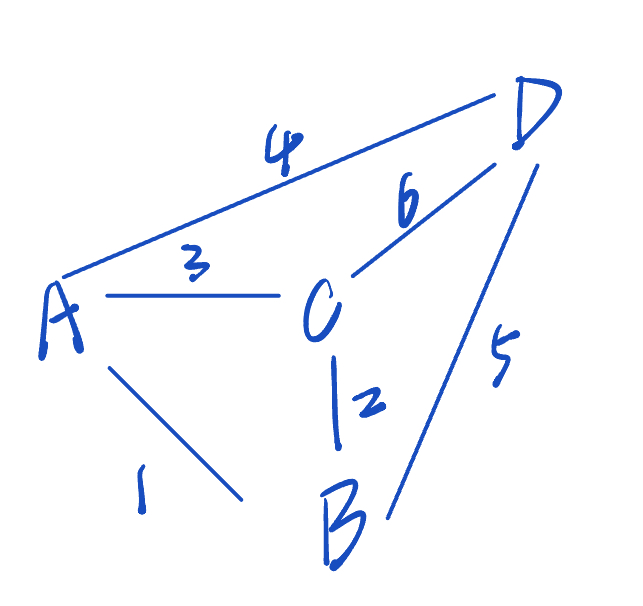
start 设做 A

把 A 放到已访问的列表。

未访问的列表里：B，C，D

把与 A 相连的边全部放到 edge_heap里，作为候选边。

edge_heap = [(4,A,D),(3,A,C),(1,A,B)]

while 1：

1. 候选边列表把目前最小边弹出。cost, u, v = 1,A,B

2. B 不在已访问的列表里面。

3. 把这条边加入最小生成树。spanning_tree = [A,B,1]

4. 把 B 添加到已访问的列表，从未访问的列表移除。

5. 对于与 B 相连的所有边：如果另一个节点在未访问列表里，加入候选边列表 [(4,A,D),(3,A,C),(2,B,C),(5,B,D)]

while 2:

1. 候选边列表把目前最小边弹出。cost, u, v = 2,B,C
2. C 不在已访问的列表里面。
3. 添加到生成树里。spanning_tree = [A,B,1], [B,C,2]
4. 把C添加到已访问列表，从未访问的列表移除。
5. 对于与 C相连的所有边，如果另一个节点没有被访问过，加入候选列表 [(4,A,D),(3,A,C),(5,B,D),(6,C,D)]

while 3:

1. 候选边列表把目前最小边弹出。cost, u, v = 3,A,C
2. C 在已访问列表里。跳过。

while 4：

1. 候选边列表把目前最小边弹出。cost, u, v = 4,A,D
2. D不在已访问的列表里
3. 添加到生成树。spanning_tree = [A,B,1], [B,C,2],[A,D,4]
4. 把 D 添加到已访问列表里。
5. 对于与D相连的所有边，进行遍历。结果邻居节点都在已访问列表。跳过

while 5:

1. 候选边列表把目前最小边弹出。cost,u,v = 5,B,D
2. D 已经在已访问的列表里。跳过

while 6：

同 5

最后生成树里的边：

spanning_tree = spanning_tree = [A,B,1], [B,C,2],[A,D,4]

代码

import heapq


def prim(graph, start):
    reached_set = set([start_node])  # 已经访问的节点集合
    unreached_set = set(graph.keys()) - reached_set  # 未访问的节点集合
    spanning_tree = []
    edge_heap = []

    for neighbor, cost in graph[start].items():
        heapq.heappush(edge_heap, (cost, start, neighbor))

    while unreached_set:
        cost, u, v = heapq.heappop(edge_heap)

        if v in unreached_set:
            spanning_tree.append((u, v, cost))
            reached_set.add(v)
            unreached_set.remove(v)

            for neighbor, edge_cost in graph[v].items():
                if neighbor in unreached_set:
                    heapq.heappush(edge_heap, (edge_cost, v, neighbor))
    return spanning_tree


# 示例图结构（邻接表表示）
graph = {
    'A': {'B': 1, 'C': 3, 'D': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 3, 'B': 2, 'D': 6},
    'D': {'A': 4, 'C': 6, 'B': 5}
}

# 调用 Prim 算法，选择起始节点为 'A'
start_node = 'A'
mst = prim(graph, start_node)

# 输出最小生成树的边
print("最小生成树的边：")
for edge in mst:
    print(f"{edge[0]} - {edge[1]} (权重: {edge[2]})")

def prim_algorithm(graph, start_node):
    # 初始化 ReachSet、UnReachSet 和 SpanningTree
    reach_set = {start_node}  # 已经被包含在生成树中的节点
    unreach_set = set(graph.keys()) - reach_set  # 尚未被包含的节点
    spanning_tree = []  # 用于存储最小生成树的边
    total_cost = 0  # 最小生成树的总权重

    while unreach_set:
        # 寻找符合条件的边 (x, y)：
        # x 属于 ReachSet, y 属于 UnReachSet, 并且具有最小的权重
        min_edge = None
        min_cost = float('inf')
        for x in reach_set:
            for y, cost in graph[x].items():
                if y in unreach_set and cost < min_cost:
                    min_edge = (x, y)
                    min_cost = cost

        # 将最小边加入生成树
        if min_edge:
            x, y = min_edge
            spanning_tree.append((x, y, min_cost))  # 加入最小生成树
            total_cost += min_cost  # 累加边的权重

            # 更新 ReachSet 和 UnReachSet
            reach_set.add(y)
            unreach_set.remove(y)

    return spanning_tree, total_cost


# 示例图（邻接表表示）
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}

# 运行算法
start_node = 'A'
spanning_tree, total_cost = prim_algorithm(graph, start_node)

# 输出结果
print("最小生成树的边:", spanning_tree)
print("最小生成树的总权重:", total_cost)

Kruskal’s algorithm

class Edge:
    def __init__(self, u, v, weight):
        self.u = u
        self.v = v
        self.weight = weight


class unionfind:
    def __init__(self, vertices):
        self.parent = {vertex: vertex for vertex in vertices}

    def find(self, vertex):
        if self.parent[vertex] != vertex:
            self.parent[vertex] = self.find(self.parent[vertex])
        return self.parent[vertex]

    def union(self, u, v):
        root_u = self.find(u)
        root_v = self.find(v)
        if root_u == root_v:
            return False
        self.parent[root_v] = root_u
        return True


def kruskal(vertices, edge):
    uf = unionfind(vertices)
    sorted_edges = sorted(edge, key=lambda edge: edge.weight)
    mst = []
    for edge in sorted_edges:
        if uf.union(edge.u, edge.v):
            mst.append(edge)
            if len(mst) == len(vertices) - 1:
                break
        else:
            continue
    return mst

if __name__ == '__main__':
    vertices = ['A', 'B', 'C', 'D', 'E', 'F']
    edges = [
        Edge('A', 'B', 4),
        Edge('A', 'F', 2),
        Edge('B', 'C', 6),
        Edge('B', 'F', 5),
        Edge('C', 'D', 3),
        Edge('C', 'E', 7),
        Edge('D', 'E', 8),
        Edge('D', 'F', 4),
        Edge('E', 'F', 1)
    ]

    mst = kruskal(vertices, edges)
    print("最小生成树的边为：")
    total_weight = 0
    for edge in mst:
        print(f"{edge.u} -> {edge.v} -> {edge.weight}")
        total_weight += edge.weight
    print(f"最小生成树的权重总和：{total_weight}")

# 定义 Kruskal 算法
class Graph:
    def __init__(self, vertices):
        self.V = vertices  # 图的节点数
        self.edges = []    # 图的边集（格式：[权重, 起点, 终点]）

    # 添加边
    def add_edge(self, u, v, weight):
        self.edges.append([weight, u, v])

    # 查找集合的根节点（带路径压缩）
    def find(self, parent, i):
        if parent[i] == i:
            return i
        return self.find(parent, parent[i])

    # 合并两个集合（带秩优化）
    def union(self, parent, rank, x, y):
        xroot = self.find(parent, x)
        yroot = self.find(parent, y)

        # 根据秩合并
        if rank[xroot] < rank[yroot]:
            parent[xroot] = yroot
        elif rank[xroot] > rank[yroot]:
            parent[yroot] = xroot
        else:
            parent[yroot] = xroot
            rank[xroot] += 1

    # Kruskal 算法实现
    def kruskal(self):
        # 初始化结果集
        result = []

        # 将边按权重排序
        self.edges = sorted(self.edges, key=lambda item: item[0])

        # 初始化 parent 和 rank
        parent = []
        rank = []

        for node in range(self.V):
            parent.append(node)
            rank.append(0)

        # 选择的边数量
        e = 0
        i = 0  # edges 索引

        # 当选定的边数小于节点数 - 1
        while e < self.V - 1:
            # 选择权重最小的边
            weight, u, v = self.edges[i]
            i += 1

            # 查找两个节点的集合
            x = self.find(parent, u)
            y = self.find(parent, v)

            # 如果不在同一集合，加入结果集并合并
            if x != y:
                e += 1
                result.append((u, v, weight))
                self.union(parent, rank, x, y)

        # 返回最小生成树的边集和权重
        return result


# 示例：使用 Kruskal 算法计算最小生成树
g = Graph(5)
g.add_edge(0, 1, 1)
g.add_edge(0, 2, 2)
g.add_edge(1, 3, 3)
g.add_edge(3, 4, 4)
g.add_edge(2, 4, 8)

mst = g.kruskal()
print("最小生成树的边集:")
for u, v, weight in mst:
    print(f"边 {u}-{v}, 权重: {weight}")

Week 7

1. Optimal Greedy Algorithms

Dijkstra’s Algorithm

详情见上周。

Scheduling

activities = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
start_times = [2, 4, 1, 6, 4, 6, 7, 9, 9, 3, 13]
finish_times = [5, 6, 7, 9, 9, 10, 11, 12, 13, 14, 15]

def greedy(activity, start_time, finish_time):
    n = len(activities)
    solution = []
    solution.append(activity[0])
    k = 0

    for i in range(1, n):
        if start_time[i] >= finish_time[k]:
            solution.append(activities[i])
            k = i

    return solution

selected_activities = greedy(activities, start_times, finish_times)
print("被选择的活动:", selected_activities)  # 输出被选择的活动编号

2. Non-optimal Greedy Algorithms

Knapsack Peoblem

1. 贪心算法

def knapSack(W, wt, val):
    result = 0
    i = 0
    weight = W
    while (weight - wt[i]) > 0:  # check if the weight minus current weight is greater than 0
        currentItem = val[i]
        currentWeight = wt[i]
        weight = weight - currentWeight
        result += currentItem
        i = i + 1
    return result


val = [60, 100, 120]  # sorted value list
wt = [10, 20, 30]  # sorted weight list
W = 50  # capacity
print(knapSack(W, wt, val))  # call and print

2. Optimal

import copy

result = []

def combination(target, data):
    for i in range(len(data)):
        new_target = copy.copy(target)
        new_data = copy.copy(data)
        new_target.append(data[i])
        result.append(new_target)
        new_data = new_data[i+1:]
        combination(new_target, new_data)


def get_best_knapsack(found_items, weight_limit):
    weight_list = []
    value_list = []
    for i in result:
        weight = 0
        value = 0
        for j in i:
            for item in found_items:
                if item['name'] == j:
                    weight += item['weight']
                    value += item['value']
        weight_list.append(weight)
        value_list.append(value)

    pi = 0
    best_knapsack = weight_list[0]
    for i in range(len(value_list)):
        current_weight = weight_list[i]
        if current_weight > best_knapsack and current_weight <= weight_limit:
            best_knapsack = current_weight
            pi = i
    print('best knapsack load is %s with a weight of %slbs and a value of £%s' \
          % (result[pi], weight_list[pi], value_list[pi]))

def main():
    found_items = [
        {'name': 'Item1', 'weight': 10, 'value': 60},
        {'name': 'Item2', 'weight': 20, 'value': 100},
        {'name': 'Item3', 'weight': 30, 'value': 120}
    ]
    weight_limit = 50
    target = []
    data = ['Item1', 'Item2', 'Item3']
    combination(target, data)
    get_best_knapsack(found_items, weight_limit)

main()

3. Knapsack With Splits

# 注释：假设物品是1公斤单位的多重物品，背包最大承重限制
def generate_composition(inventory, weight_limit):
    composition = []  # 用于存储背包中的所有物品元素，按1公斤单位分解
    for item in inventory:  # 遍历库存中的每个物品
        for i in range(item['weight']):  # 将物品拆分为每一个1公斤单位，并添加到composition列表中
            composition.append(item)
    
    # 如果背包中的物品数量超过重量限制，则截断多余的物品
    composition = composition[:weight_limit]  

    result = []  # 用于存储最终结果（去重后的物品列表）
    # 遍历库存中的每个物品
    for item in inventory:
        item['comp_quantity'] = composition.count(item)  # 计算当前物品在背包中出现的次数
        if item not in result:  # 如果该物品还没有出现在结果列表中
            result.append(item)  # 将该物品添加到结果列表中

    return result  # 返回去重后的物品列表及其数量


def generate_knapsack(inventory, weight_limit):
    # 如果传入的库存为空，则使用默认的库存
    if not inventory:
        inventory = example_inventory  

    # 通过调用generate_composition函数，计算并获取最优背包载荷
    comp = generate_composition(inventory, weight_limit)

    string = ''  # 用于构建返回的字符串，显示背包中的物品
    # 遍历所有物品，输出每个物品的数量和名称
    for item in comp:
        if item['comp_quantity'] > 0:  # 如果物品的数量大于0
            string += '{}kg of {}, '.format(
                str(item['comp_quantity']), item['name'])  # 将物品的数量和名称格式化到字符串中

    # 如果背包中有物品，去掉最后的逗号和空格
    if string:
        string = string[:-2]
    else:
        string = "No materials"  # 如果背包没有物品，显示"No materials"

    # 返回背包的内容描述字符串
    return 'Robber\'s knapsack contains: %s.' % string


def main():
    # 模拟库存物品列表，每个物品包含名称、重量和价值
    found_items = [
        {'name': 'Item_1', 'weight': 60, 'value': 60},
        {'name': 'Item_2', 'weight': 20, 'price': 100},
        {'name': 'Item_3', 'weight': 30, 'price': 120}
    ]

    weight_limit = 50  # 背包的最大承重限制
    inventory = found_items  # 设置库存为模拟的物品列表

    # 调用generate_knapsack函数，输出背包中物品的数量和名称
    print(generate_knapsack(inventory, weight_limit))


# 主程序入口
if __name__ == '__main__':
    main()  # 执行主函数

3. Maximum root to leaf sum

Greedy

# 定义一个二叉树的节点类
class Node:
    def __init__(self, data):
        self.data = data  # 节点的数据
        self.left = None  # 左子节点
        self.right = None  # 右子节点

    def __repr__(self):
        return str(self.data)  # 输出节点数据，方便打印节点时查看

# 计算二叉树的最大路径和的函数（基于贪心选择法）
def greedy_max_sum(root):
    currentNode = root  # 从根节点开始
    solution = []  # 存储路径的列表
    totalSum = root.data  # 初始化路径和为根节点的数据
    solution.append(root.data)  # 将根节点的数据加入到路径中

    # 遍历二叉树，直到找到叶子节点（没有子节点的节点）
    while currentNode.left != None or currentNode.right != None:
        if currentNode.left != None and currentNode.right != None:  # 当前节点有左右两个子节点
            # 比较左子节点和右子节点的值，选择较大的一个继续向下遍历
            if currentNode.left.data > currentNode.right.data:  # 如果左子节点的值大于右子节点
                solution.append(currentNode.left.data)  # 将左子节点的数据加入到路径中
                totalSum += currentNode.left.data  # 将左子节点的数据加到总和中
                currentNode = currentNode.left  # 更新当前节点为左子节点
            else:  # 如果右子节点的值较大或相等
                solution.append(currentNode.right.data)  # 将右子节点的数据加入到路径中
                totalSum += currentNode.right.data  # 将右子节点的数据加到总和中
                currentNode = currentNode.right  # 更新当前节点为右子节点
        elif currentNode.left != None:  # 如果当前节点只有左子节点
            solution.append(currentNode.left.data)  # 将左子节点的数据加入到路径中
            totalSum += currentNode.left.data  # 将左子节点的数据加到总和中
            currentNode = currentNode.left  # 更新当前节点为左子节点
        else:  # 如果当前节点只有右子节点
            solution.append(currentNode.right.data)  # 将右子节点的数据加入到路径中
            totalSum += currentNode.right.data  # 将右子节点的数据加到总和中
            currentNode = currentNode.right  # 更新当前节点为右子节点

    # 返回路径及其对应的总和
    return solution, totalSum


# 程序的入口点
if __name__ == '__main__':
    # 构建一个二叉树
    root = Node(1)  # 根节点为1
    root.left = Node(2)  # 根节点的左子节点为2
    root.right = Node(3)  # 根节点的右子节点为3
    root.left.left = Node(5)  # 左子节点的左子节点为5
    root.left.right = Node(7)  # 左子节点的右子节点为7
    root.right.right = Node(4)  # 右子节点的右子节点为4

    # 调用greedy_max_sum函数，计算路径和
    print(greedy_max_sum(root))

Optimal

# 定义二叉树节点
class Node:
    def __init__(self, data):
        self.data = data  # 节点存储的数据
        self.left = None   # 左子节点
        self.right = None  # 右子节点

    # 节点的字符串表示方法，用于调试或输出
    def __repr__(self):
        return str(self.data)


# 全局变量，用于存储找到的最大路径
result = []


# 递归地找出从根节点到叶子节点路径和等于给定值的路径
def print_max_sum_tree_path(root, summ):
    # 当路径和正好为0时，返回True，表示找到了正确的路径
    if summ == 0:
        return True

    # 如果节点为空，返回False
    if root is None:
        return False

    # 递归查找左子树和右子树是否有符合条件的路径
    left = print_max_sum_tree_path(root.left, summ - root.data)
    right = print_max_sum_tree_path(root.right, summ - root.data)

    # 如果左子树或右子树找到符合条件的路径，就把当前节点加入结果路径
    if left or right:
        result.insert(0, root.data)  # 将当前节点添加到路径的开头

    # 返回是否有符合条件的路径
    return left or right


# 递归计算从当前节点到叶子节点的最大路径和
def max_sum_root_to_leaf(root):
    # 如果当前节点为空，返回0（无路径和）
    if not root:
        return 0

    # 如果左子节点为空，则最大路径和是右子树的最大路径和
    if root.left is None:
        max_sum_left = 0
    else:
        # 否则，递归求左子树的最大路径和
        max_sum_left = max_sum_root_to_leaf(root.left)

    # 如果右子节点为空，则最大路径和是左子树的最大路径和
    if root.right is None:
        max_sum_right = 0
    else:
        # 否则，递归求右子树的最大路径和
        max_sum_right = max_sum_root_to_leaf(root.right)

    # 返回左子树和右子树中的较大者，加上当前节点的值
    return max(max_sum_left, max_sum_right) + root.data


# 找出最大路径和并输出路径
def find_max_sum_and_print(root):
    # 计算从根节点到叶子节点的最大路径和
    max_sum = max_sum_root_to_leaf(root)
    # 输出最大路径和
    print_max_sum_tree_path(root, max_sum)
    # 打印最大路径和
    print("maximum sum from root to leaf is:", max_sum)


# 主函数（驱动程序）
if __name__ == '__main__':
    # 创建二叉树
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(5)
    root.left.right = Node(7)
    root.right.right = Node(4)

    # 找到并打印最大路径和
    find_max_sum_and_print(root)
    # 打印路径
    print('path is:', result)