高级算法——第8周查漏补缺
原创2024年11月11日大约 10 分钟
Lecture 08
时间复杂度
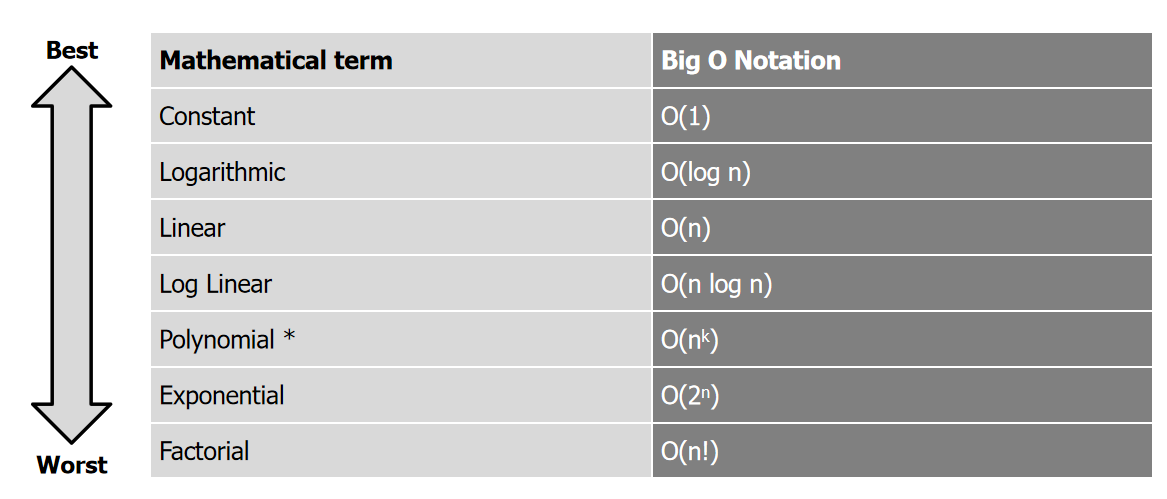
1. constant
a = [11, 22, 33, 44, 55]
b = [10, 8, 7]
print(a[0])
print(b[0])如插值搜索(最好情况)的时间复杂度。
2. Logarithmic
如二分搜索的时间复杂度。
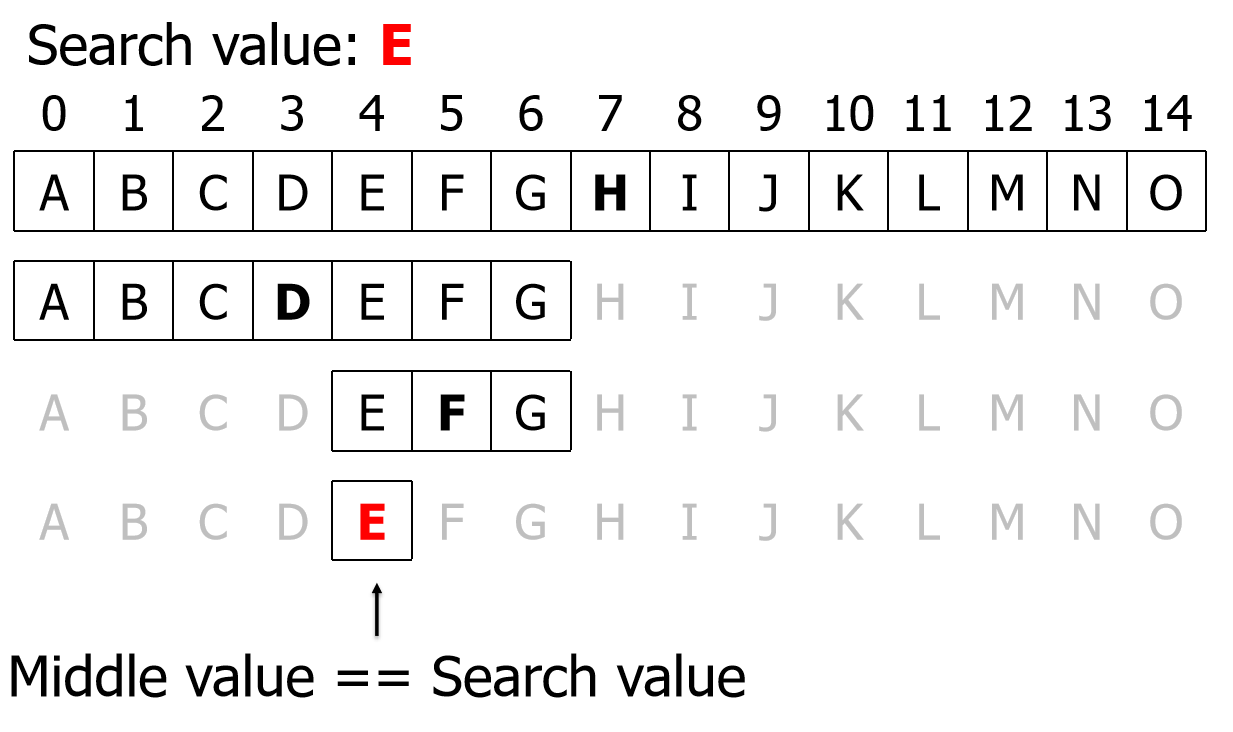
每次都会将要操作的对象减半。符合 log 函数的定义。
3. linear
伪代码:
FIND (A, target)
n ← A.length
FOR (i FROM 0 TO n)
IF (A[i]=target)
RETURN TRUE
RETURN FALSE4. log linear
- O (n log n) means do O (log n) n times.
- So e.g. do 6 binary searches
def linear_log_recur(n: int) -> int:
"""线性对数阶"""
if n <= 1:
return 1
# 一分为二,子问题的规模减小一半
count = linear_log_recur(n // 2) + linear_log_recur(n // 2)
# 当前子问题包含 n 个操作
for _ in range(n):
count += 1
return count5. polynomial
嵌套循环。
插值排序:
INSERTION-SORT(A)
for j ← 1 to length[A] (n times)
key ← A[j] (n times)
i ← j-1 (n times)
while i > 0 and A[i] > key (n*n times)
A[i+1] ← A[i] (n*n times)
i ← i+1 (n*n times)
A[i+1] ← key (n times)6. exponential
斐波那契数列:
FIBONACCI(num)
IF num <=1
return num
return FIBONACCI (num-2) + FIBONACCI(num-1)7. factorial
def factorial_recur(n):
if n == 0:
return 1
count = 0
for i in range(n):
count += factorial_recur(n - 1)
return countNP-Hard problems
- NP - Non deterministic Polynomial time complexity
- A non deterministic algorithm can exhibit different behaviours on different runs for the same input variables.
1. Exhaustive search —— Travelling saleman
这是关于**穷举搜索(Exhaustive Search)**的概述图片,介绍了穷举搜索的一些特点。这类搜索方法遍历所有可能的解,以找到满足问题条件的解。穷举搜索适用于问题规模较小的情况,因为它的时间和空间成本会随着问题规模的增加而迅速增长。
穷举法:
import itertools # 导入Python的itertools库,用于处理迭代器
# 定义边的列表,即城市之间的距离
dists = [
['A', 'B', 20], ['A', 'C', 35], ['A', 'D', 42],
['B', 'A', 20], ['B', 'C', 34], ['B', 'D', 30],
['C', 'A', 35], ['C', 'B', 34], ['C', 'D', 12],
['D', 'A', 42], ['D', 'B', 30], ['D', 'C', 12]
]
# 定义函数,获取所有可能的排列(即可能的路径)
def get_and_convert_perm_list(dests):
# 使用itertools.permutations生成所有排列
perm_list = list(itertools.permutations(dests)) # 生成一个包含所有排列的列表(列表中的元素是元组)
new_perm_list = [] # 定义一个新的列表,用于存储列表形式的排列
# 将元组转换为列表(方便后续处理)
for item in perm_list:
new_perm_list.append(list(item))
return new_perm_list # 返回转换后的排列列表
# 定义函数,计算每条路径的总距离
def TSP_get_dists(dests, dists):
results = [] # 用于存储所有结果的列表
perm_list = get_and_convert_perm_list(dests) # 获取所有排列列表
# 遍历每一个排列(即一条路径)
for item in perm_list:
item.append(item[0]) # 将起点添加到路径末尾,形成回路
total_dist = 0 # 初始化总距离
# 计算该路径的总距离
for i in range(len(item) - 1): # 遍历路径中的每对相邻城市
for dist in dists: # 匹配路径中的每对城市与距离列表中的城市对
if item[i] == dist[0] and item[i + 1] == dist[1]: # 找到匹配的城市对
total_dist = total_dist + dist[2] # 将对应的距离加到总距离中
# 如果已经遍历完该路径,记录总距离
if i == len(item) - 2:
item.append(total_dist) # 将总距离添加到路径的末尾
print(item) # 打印路径及其总距离,便于观察
results.append(item) # 将该路径及总距离添加到结果列表中
return results # 返回所有结果的列表
# 调用函数,计算包含城市A、B、C、D的所有路径及其总距离
TSP_get_dists(['A', 'B', 'C', 'D'], dists)2. Heuristics ——Travelling saleman
启发式函数能在合理的时间范围内产生一个足以解决问题的解决方案。该解决方案可能不是最佳解决方案,但可能仍然很有价值,因为它不需要很长时间就能找到。
销售员从一个随机城市开始,访问最近的城市,直到访问完所有城市为止
# 定义城市之间的距离
dists = [
['A', 'B', 20], ['A', 'C', 35], ['A', 'D', 42],
['B', 'A', 20], ['B', 'C', 34], ['B', 'D', 30],
['C', 'A', 35], ['C', 'B', 34], ['C', 'D', 12],
['D', 'A', 42], ['D', 'B', 30], ['D', 'C', 12]
]
# 定义一个函数,用于查找两个城市之间的距离
def find_distance(city1, city2, dists):
for dist in dists:
if dist[0] == city1 and dist[1] == city2:
return dist[2]
return float('inf') # 如果没有找到对应的距离,返回无穷大
# 定义最近邻算法的主函数
def nearest_neighbour(start, dists):
unvisited = ['A', 'B', 'C', 'D'] # 未访问的城市
visited = [] # 已访问的城市
connections = [] # 记录访问路径的连接
u = start # 从起始城市开始
visited.append(u) # 将起始城市添加到已访问列表
unvisited.remove(u) # 从未访问列表中移除起始城市
# 当还有未访问的城市时,继续循环
while unvisited:
# 找到从当前城市到未访问城市的最小距离的边
min_distance = float('inf')
next_city = None
for city in unvisited:
distance = find_distance(u, city, dists) # 查找距离
if distance < min_distance: # 如果找到更小的距离
min_distance = distance
next_city = city
# 更新当前城市为找到的下一个城市
u = next_city
connections.append((visited[-1], u, min_distance)) # 添加边到连接列表
visited.append(u) # 将找到的城市添加到已访问列表
unvisited.remove(u) # 从未访问列表中移除该城市
return connections # 返回完整的访问路径和距离
# 调用函数,并输出结果
start_city = 'A'
route = nearest_neighbour(start_city, dists)
# 输出路径
print("访问路径及距离:")
for connection in route:
print(f"从 {connection[0]} 到 {connection[1]} 的距离为 {connection[2]}")3. Local search
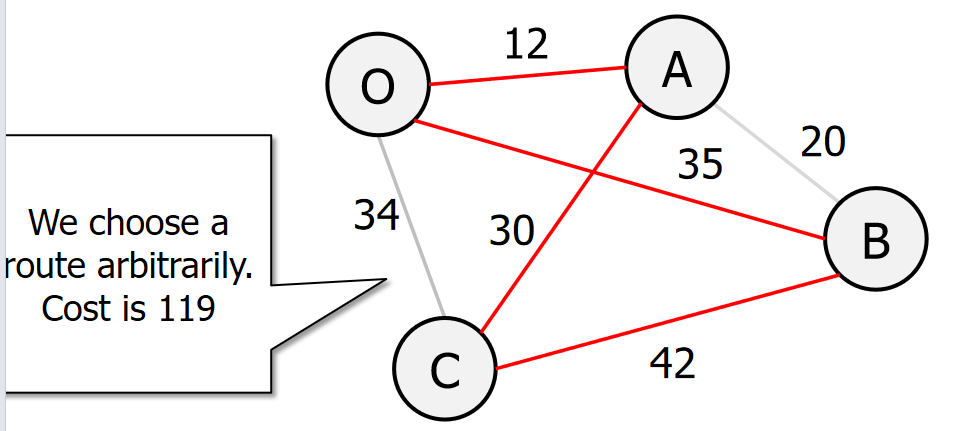
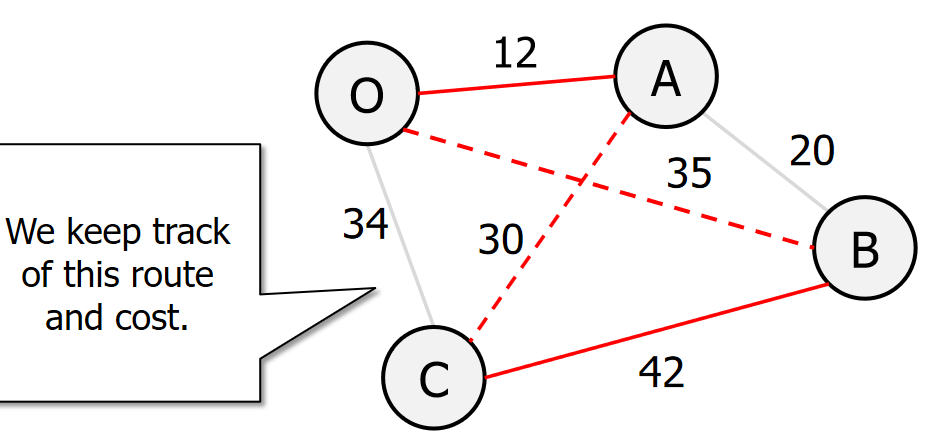
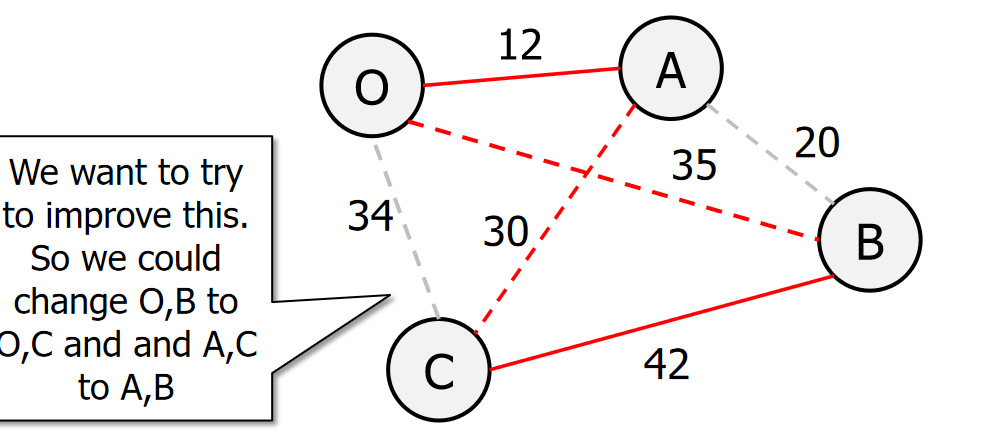
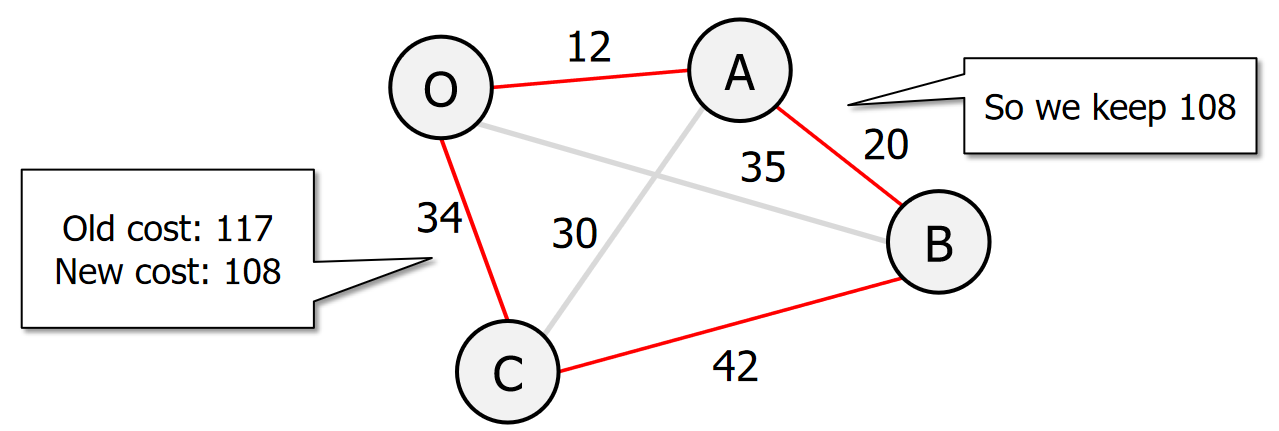
import random
# 定义城市之间的距离
dists = {
('A', 'B'): 20, ('A', 'C'): 35, ('A', 'D'): 42,
('B', 'A'): 20, ('B', 'C'): 34, ('B', 'D'): 30,
('C', 'A'): 35, ('C', 'B'): 34, ('C', 'D'): 12,
('D', 'A'): 42, ('D', 'B'): 30, ('D', 'C'): 12
}
# 定义计算路径总距离的函数
def distance(route, dists):
total_distance = 0
for i in range(len(route) - 1):
total_distance += dists[(route[i], route[i+1])]
total_distance += dists[(route[-1], route[0])] # 回到起始点
return total_distance
# 定义变异函数,用于2-opt交换
def mutate_2_opt(route):
i, j = random.sample(range(1, len(route)), 2)
if i > j:
i, j = j, i
# 执行2-opt交换
new_route = route[:i] + route[i:j+1][::-1] + route[j+1:]
return new_route
# 定义TSP的局部搜索算法
def local_search_tsp(startroute, dists, i_max=100):
current_route = startroute # 初始化为起始路径
min_distance = distance(current_route, dists) # 计算初始路径的总距离
for i in range(i_max):
new_route = mutate_2_opt(current_route) # 生成一个新路径
new_distance = distance(new_route, dists) # 计算新路径的距离
if new_distance < min_distance: # 如果新路径更短,则更新最优解
min_distance = new_distance
current_route = new_route
return current_route, min_distance # 返回最优路径和最短距离
# 定义初始路径
start_route = ['A', 'B', 'C', 'D']
# 调用局部搜索算法并输出结果
best_route, best_distance = local_search_tsp(start_route, dists)
print("最优路径:", best_route)
print("最优路径的总距离:", best_distance)4. Simulated annealing
import math
import random
# 定义城市之间的距离
dists = {
('A', 'B'): 20, ('A', 'C'): 35, ('A', 'D'): 42,
('B', 'A'): 20, ('B', 'C'): 34, ('B', 'D'): 30,
('C', 'A'): 35, ('C', 'B'): 34, ('C', 'D'): 12,
('D', 'A'): 42, ('D', 'B'): 30, ('D', 'C'): 12
}
# 定义计算路径总距离的函数
def distance(route, dists):
total_distance = 0
for i in range(len(route) - 1):
# 累加相邻城市之间的距离
total_distance += dists[(route[i], route[i + 1])]
# 加上最后一个城市回到起始城市的距离
total_distance += dists[(route[-1], route[0])]
return total_distance
# 定义变异函数,用于2-opt交换
def mutate_2_opt(route):
# 随机选择两个索引进行2-opt交换
i, j = random.sample(range(1, len(route)), 2)
if i > j:
i, j = j, i
# 生成新的路径,将i到j之间的部分反转
new_route = route[:i] + route[j:i-1:-1] + route[j+1:]
return new_route
# 模拟退火算法
def simulated_annealing(start_route, dists, initial_temp=1000, cooling_rate=0.995, min_temp=0.01):
current_route = start_route # 当前路径初始化为起始路径
current_distance = distance(current_route, dists) # 当前路径的总距离
best_route = current_route # 初始化最优路径
best_distance = current_distance # 初始化最优距离
temperature = initial_temp # 设置初始温度
# 当温度高于最低温度时,持续迭代
while temperature > min_temp:
# 生成一个新的路径,并计算其距离
new_route = mutate_2_opt(current_route)
new_distance = distance(new_route, dists)
# 判断是否接受新解:若新解更优则接受,若更差则以一定概率接受
if new_distance < current_distance or random.random() < math.exp((current_distance - new_distance) / temperature):
current_route = new_route # 接受新解作为当前解
current_distance = new_distance
# 如果新解优于最优解,则更新最优解
if new_distance < best_distance:
best_route = new_route
best_distance = new_distance
# 按照冷却速率降低温度
temperature *= cooling_rate
return best_route, best_distance # 返回最终的最优路径和最优距离
# 定义初始路径
start_route = ['A', 'B', 'C', 'D']
# 调用模拟退火算法并输出结果
best_route, best_distance = simulated_annealing(start_route, dists)
print("最优路径:", best_route)
print("最优路径的总距离:", best_distance)5. Grasp
整体思路:
- 调用 random 库和 math 库。
- 首先封装一个函数算出两个城市之间的距离
- 再封装一个函数算出一条路线上城市的总距离
greedy_construct_solution用于随机构成一个初始路径local_search找到局部最优解,这个范围是局部的,因为循环次数有限。- 不断搜索局部最优解,找到最优的局部最优解。
import random
import math
# 计算两个城市之间的欧几里得距离
def calculate_distance(city1, city2):
"""
计算城市 city1 和 city2 之间的欧几里得距离。
:param city1: 城市1的坐标 (x1, y1)
:param city2: 城市2的坐标 (x2, y2)
:return: 两个城市之间的距离
"""
return math.sqrt((city1[0] - city2[0]) ** 2 + (city1[1] - city2[1]) ** 2)
# 计算路径的总距离
def total_distance(path, cities):
"""
计算给定路径的总距离。
:param path: 城市访问顺序的列表
:param cities: 城市的坐标列表
:return: 路径的总距离
"""
distance = 0
for i in range(len(path)):
city1 = cities[path[i]]
city2 = cities[path[(i + 1) % len(path)]]
distance += calculate_distance(city1, city2)
return distance
# 随机化贪心构造初始解
def greedy_construct_solution(cities):
"""
使用随机化贪心算法构造一个初始解。
:param cities: 城市的坐标列表
:return: 构造出的初始解路径
"""
num_cities = len(cities)
unvisited = list(range(num_cities)) # 未访问的城市列表
solution = []
current_city = random.choice(unvisited) # 随机选择一个起始城市
solution.append(current_city)
unvisited.remove(current_city)
# 构造路径,直到所有城市都被访问
while unvisited:
# 构建候选列表,并按距离排序
candidate_list = []
for city in unvisited:
distance = calculate_distance(cities[current_city], cities[city])
candidate_list.append((city, distance))
# 按距离排序,并构造受限候选列表 (RCL)
candidate_list.sort(key=lambda x: x[1])
rcl_size = max(1, len(candidate_list) // 3) # 选择前 1/3 的较优解作为 RCL
rcl = candidate_list[:rcl_size]
# 从 RCL 中随机选择一个城市
next_city = random.choice(rcl)[0]
solution.append(next_city)
unvisited.remove(next_city)
current_city = next_city
return solution
# 局部搜索优化解(2-opt 算法)
def local_search(solution, cities):
"""
使用 2-opt 算法进行局部搜索优化。
:param solution: 初始解路径
:param cities: 城市的坐标列表
:return: 优化后的路径
"""
best_solution = solution[:]
best_distance = total_distance(best_solution, cities)
improved = True
while improved:
improved = False
# 2-opt 搜索:交换路径中的两个边
for i in range(1, len(solution) - 1):
for j in range(i + 1, len(solution)):
if j - i == 1: # 相邻城市跳过
continue
# 交换两个城市之间的路径
new_solution = best_solution[:]
new_solution[i:j] = best_solution[i:j][::-1]
new_distance = total_distance(new_solution, cities)
if new_distance < best_distance:
best_solution = new_solution[:]
best_distance = new_distance
improved = True
return best_solution
# GRASP 主函数
def grasp_tsp(cities, max_iterations):
"""
使用 GRASP 算法求解旅行商问题。
:param cities: 城市的坐标列表
:param max_iterations: 最大迭代次数
:return: 最优路径和最短距离
"""
best_solution = None
best_distance = float('inf')
for _ in range(max_iterations):
# 构造初始解
initial_solution = greedy_construct_solution(cities)
# 局部搜索优化解
improved_solution = local_search(initial_solution, cities)
# 计算路径总距离
current_distance = total_distance(improved_solution, cities)
# 更新全局最优解
if current_distance < best_distance:
best_solution = improved_solution
best_distance = current_distance
return best_solution, best_distance
# 主程序
if __name__ == "__main__":
# 定义城市的坐标 (x, y)
cities = [
(0, 0), (1, 5), (5, 2), (6, 6), (8, 3),
(3, 7), (7, 9), (4, 4), (9, 1), (2, 8)
]
# 最大迭代次数
max_iterations = 100
# 执行 GRASP 算法求解 TSP
best_solution, best_distance = grasp_tsp(cities, max_iterations)
# 输出最优路径和最短距离
print("最优路径:", best_solution)
print("最短距离:", best_distance)