高级算法——第4,5周查漏补缺
原创2024年11月6日大约 10 分钟
week 04
1. BST 的查找,插入与删除
循环的——查找插入删除
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
def find(self, key):
cur = self.root
while cur != None:
if cur.val == key:
return cur
elif cur.val > key:
cur = cur.left
else:
cur = cur.right
return False
def insert(self, key):
cur, pre = self.root, None
while cur != None:
if cur.val == key:
return
pre = cur
if cur.val > key:
cur = cur.left
elif cur.val < key:
cur = cur.right
node = TreeNode(key)
if pre.val > key:
pre.left = node
else:
pre.right = node
def delete(self, key):
cur, pre = self.root, None
while cur.val != key:
if cur is None:
return False
pre = cur
if cur.val > key:
cur = cur.left
else:
cur = cur.right
if cur.left is None or cur.right is None:
child = cur.right or cur.left
if pre.left == cur:
pre.left = child
else:
pre.right = child
else:
replace_cur = self.find_min(cur)
cur.val = replace_cur.val
def find_min(self, node):
if node is None:
return None
node = node.right
while node.left is not None:
node = node.left
return node
if __name__ == '__main__':
# 手动创建二叉搜索树
bst = BST()
bst.root = TreeNode(4)
bst.root.left = TreeNode(2)
bst.root.right = TreeNode(6)
bst.root.left.left = TreeNode(1)
bst.root.left.right = TreeNode(3)
bst.root.right.left = TreeNode(5)
bst.root.right.right = TreeNode(7)
bst.insert(8)
bst.delete(8)
# 测试查找节点
node = bst.find(8)
if node:
print(f"找到了节点,值为: {node.val}") # 打印该节点的值
else:
print("未找到节点")递归的——查找插入删除
class TreeNode:
"""二叉树节点类"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
def search(self, root, val):
if root is None:
return None
if val < root.val:
return self.search(root.left, val)
elif val > root.val:
return self.search(root.right, val)
else:
return root # 这里是返回了该节点的地址,而不是值
def insert(self, root, num):
if root is None:
return TreeNode(num)
if num < root.val:
root.left = self.insert(root.left, num)
elif num > root.val:
root.right = self.insert(root.right, num)
return root
def delete(self, root, key):
if root is None:
return root
if key < root.val:
root.left = self.delete(root.left, key)
elif key > root.val:
root.right = self.delete(root.right, key)
else:
if root.left is None and root.right is None:
return None
elif root.left:
return root.left
elif root.right:
return root.right
else:
min_find_num = self.find_min(root.right)
min_find_num.val = root.val
root.right = self.delete(root.right, min_find_num)
return root
def find_min(self,root):
current = root
while current.left is not None:
current = current.left
return current
if __name__ == '__main__':
bst = BST()
bst.root = bst.insert(bst.root,6)
bst.insert(bst.root, 3)
bst.insert(bst.root, 9)
bst.insert(bst.root, 1)
bst.insert(bst.root, 2)
bst.insert(bst.root, 7)
bst.insert(bst.root, 10)
bst.delete(bst.root, 5)
# 测试查找节点
node = bst.search(bst.root, 10)
if node:
print(f"找到了节点,值为: {node.val}") # 打印该节点的值
else:
print("未找到节点")2. BST 的遍历
2.1 Pre Order
res = []
def preorder(root: TreeNode):
if root is None:
return
res.append(root.val)
if root.left is not None:
preorder(root.left)
if root.right:
preorder(root.right)
preorder(n1)
print(res)2.2 In Order
res = []
def inorder(root: TreeNode):
if root is None:
return
if root.left is not None:
inorder(root.left)
res.append(root.val)
if root.right:
inorder(root.right)
inorder(n1)
print(res)2.3 Post Order
res = []
def postorder(root: TreeNode):
if root is None:
return
if root.left is not None:
inorder(root.left)
if root.right:
inorder(root.right)
res.append(root.val)
postorder(n1)
print(res)3. 广度遍历和深度遍历
3.1 广度遍历(BFS)
class TreeNode:
def __init__(self, val: int):
self.val = val
self.left = None
self.right = None
n1 = TreeNode(val=1)
n2 = TreeNode(val=2)
n3 = TreeNode(val=3)
n4 = TreeNode(val=4)
n5 = TreeNode(val=5)
n6 = TreeNode(val=6)
n7 = TreeNode(val=7)
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n3.left = n6
n3.right = n7
def level_order(root):
queue = []
if root is not None:
queue.append(root)
res = []
while queue:
node = queue.pop(0)
res.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return res
print(level_order(n1))class TreeNode:
"""二叉树节点类"""
def __init__(self, val: int):
self.val: int = val # 节点值
self.left: 'TreeNode' | None = None # 左子节点引用
self.right: 'TreeNode' | None = None # 右子节点引用
n1 = TreeNode(val=1)
n2 = TreeNode(val=2)
n3 = TreeNode(val=3)
n4 = TreeNode(val=4)
n5 = TreeNode(val=5)
n6 = TreeNode(val=6)
n7 = TreeNode(val=7)
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n3.left = n6
n3.right = n7
def level_order_recursive(root):
res = []
if root:
level_helper([root], res)
return res
def level_helper(queue, res):
if not queue:
return
node = queue.pop(0)
res.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
level_helper(queue, res)
print(level_order_recursive(n1))3.2 深度遍历(就是先中后序遍历)
5. Balanced and Unbalanced Trees 查找。无意义
6. AVL Trees
class TreeNode:
def __init__(self, val):
self.height = 0
self.val = val
self.left = None
self.right = None
def get_height(self, node):
if node is not None:
return node.height
return -1
def update_height(self, node):
return max([self.get_height(node.left), self.get_height(node.right)]) + 1
def balance_factor(self, node):
if node is None:
return 0
return self.get_height(node.left) - self.get_height(node.right)
def right_rotation(self, node):
child = node.left
grand_child = child.right
child.right = node
node.left = grand_child
self.update_height(child)
self.update_height(node)
return child
def left_rotation(self, node):
child =node.right
grand_child = child.left
child.left = node
node.right = grand_child
self.update_height(child)
self.update_height(node)
return child
def roration(self, node):
balance_factor = self.balance_factor(node)
if balance_factor > 1:
if self.balance_factor(node.left) >= 0:
self.right_rotation(node)
else:
self.left_rotation(node.left)
self.left_rotation(node)
elif balance_factor < -1:
if self.balance_factor(node.right) >= 0:
self.left_rotation(node)
else:
self.right_rotation(node.left)
self.left_rotation(node)
return node
def insert(self, val):
self._root = self.insert_helper(self._root, val)
def insert_helper(self, node, val):
if node is None:
return TreeNode(val)
if val < node.val:
node.left = self.insert_helper(node.left, val)
elif val > node.val:
node.right = self.insert_helper(node.right, val)
else:
return
self.update_height(node)
return node.rotation(node)
def delete(self, val):
self._root = self.delete_helper(self._root,val)
def delete_helper(self, node, val):
if node is None:
return
if val < node.val:
node.left = self.delete_helper(node.left, val)
elif val > node.val:
node.right = self.delete_helper(node.right,val)
else:
if node.left is None or node.right is None:
child = node.left or node.right
if child is not None:
node = child
else:
return None
else:
min_node = node.right
while min_node.left is not None:
min_node = min_node.left
node.val = min_node.val
node.right = self.delete_helper(node.right, min_node.val)
self.update_height(node)
return node.rotation(node)week 05
1. Hashing
2. linked list
数组查找好,链表插入和删除好。
双向链表 :DOUBLE LINKED LIST
循环链表:CIRCULAR LIST
双向链表插入删除查找序号;值:
自己写的(逻辑不严密)
class ListNode:
def __init__(self, val):
self.val = val
self.next = None
self.prev = None
self.L.head = None
self.L.tail = None
def insert(n0, p):
if n0.next is None:
n0.next = ListNode(p)
p.prev = n0
else:
n0.next.prev = p
p.next = n0.next
n0.next = p
p.prev = n0
def delete(p):
if
def access(head, index):
for i in range(index):
if head is None:
return None
else:
head = head.next
return head
def find_val(head, target):
if head is None:
return None
index = 0
while head is not None:
if head.val == target:
return index
else:
head = head.next
index += 1
n0 = ListNode(1)
n1 = ListNode(2)
n2 = ListNode(3)
n0.next = n1
n1.prev = n0
n1.next = n2
n2.prev = n1
node = access(n0, 1)
print(f"列表 1 号位置的节点是{node.val}")插入节点、删除节点
class ListNode:
def __init__(self, val):
self.val = val
self.next = None
self.prev = None
class linkedList:
def __init__(self):
self._L = None
self.head = None
self.tail = None
def insert(self, L, pre, p):
if L.head is None:
# 如果链表为空,初始化链表
L.head = L.tail = p
p.next = p.prev = None
else:
# 插入新节点 p 在 pre 后面
p.next = pre.next
pre.next = p
p.prev = pre
# 更新下一个节点的 prev 指针
if p.next is not None:
p.next.prev = p
# 如果 pre 是尾节点,更新尾节点
if L.tail == pre:
L.tail = p
def delete(self, L, p):
if p.prev is not None:
p.prev.next = p.next
else:
L.head = p.next
if p.next is not None:
p.next.prev = p.prev
else:
L.tail = p.prev打印、头尾节点插入、删头结点
class Node:
def __init__(self, dataval):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None # 初始化一个头结点(Initialize a head node)
def listprint(self):
printval = self.headval
while printval is not None:
print(printval.dataval)
printval = printval.nextval
# 在链表的开头插入新节点
def AtBeginning(self, newdata):
NewNode = Node(newdata) # 创建新节点
if self.headval is None:
# 链表为空时,直接让 head 指向新节点
self.headval = NewNode
else:
# 插入新节点到链表头部
NewNode.nextval = self.headval
self.headval = NewNode
def AtEnd(self, newdata):
NewNode = Node(newdata)
if self.headval is None:
self.headval = NewNode
return
else:
last = self.headval
while last.nextval:
last = last.nextval
last.nextval = NewNode
def delete_head(self):
# if linked list is empty nothing to delete
if self.headval is None:
return
# Point at the head of the linked lisr
start = self.headval
# set the head of list as the second element
self.headval = self.headval.nextval
# delete the original head of the list
del start
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Thur")
e4 = Node("Fri")
e5 = Node("Sat")
list.headval.nextval = e2
e2.nextval = e3
e3.nextval = e4
e4.nextval = e5
list.AtEnd("Sun")
list.AtBeginning("Days")
list.listprint()3. Stacks
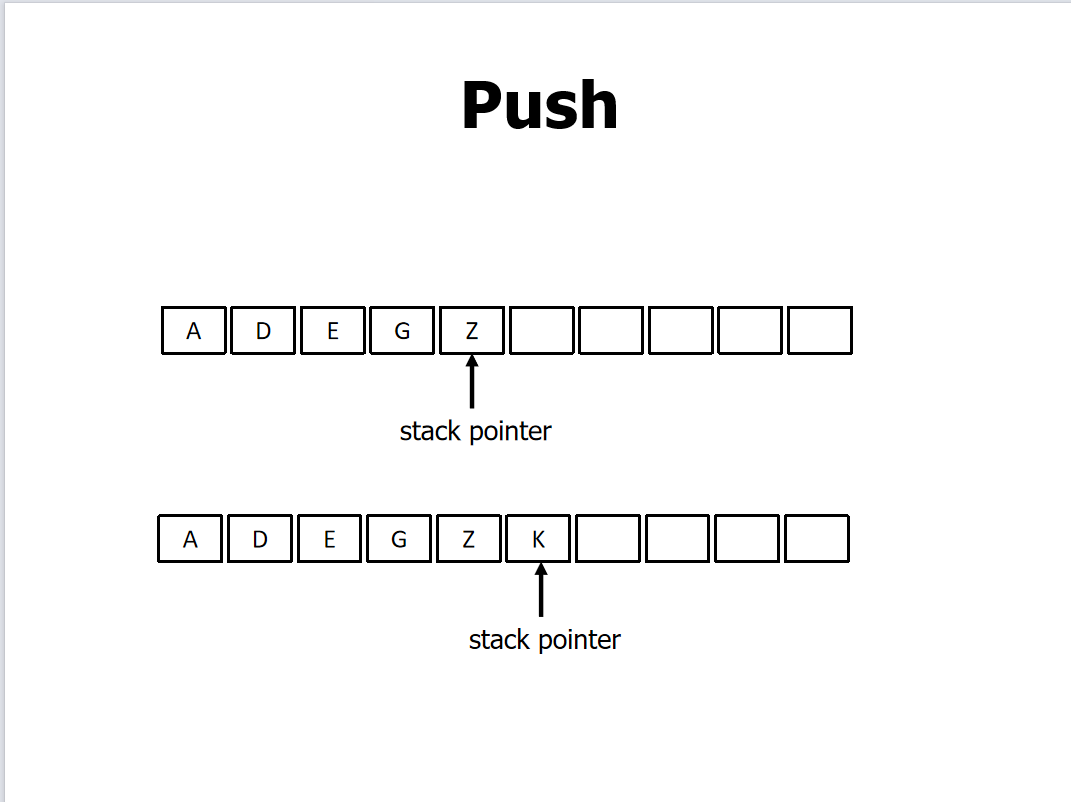
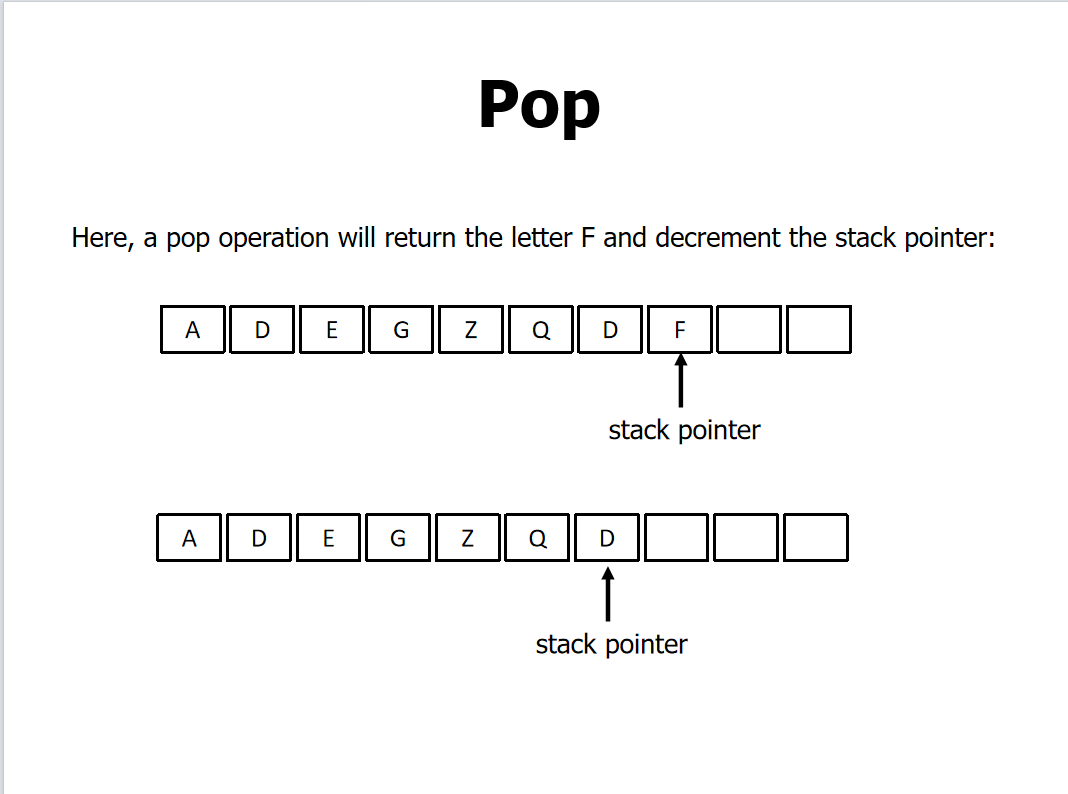
操作:入栈和出栈
堆栈指针:
- 用来索引栈里的元素
- 经常用在栈头部
- 如果推送了一个元素,指针就会递增,该元素就会被添加到顶部。
- 如果一个项目被弹出,指针将递减,该项目将返回给程序
class Stack(object):
def __init__(self):
self.stack = [0] * 100
self.top = 0
def push(self, val):
# 检查栈是否已满,如果满了则扩容
if self.top >= len(self.stack):
self.stack = self.stack + [0] * len(self.stack) # 将栈的长度翻倍
# 插入元素到栈顶位置
self.top += 1
self.stack[self.top] = val
def pop(self, val):
if self.top == -1:
raise IndexError("pop from empty stack")
self.top -= 1
return self.stack[self.top + 1] # 这个是返回弹出的栈顶元素
def peek(self):
# 检查栈是否为空
if self.top == -1:
raise IndexError("peek from empty stack")
return self.stack[self.top]
def is_empty(self):
# 判断栈是否为空
return self.top == -1
def size(self):
# 返回栈中元素的数量
return self.top + 1
def capacity(self):
# 返回栈的容量(数组长度)
return len(self.stack)
def print_stack(self):
# 打印栈中的所有元素
if self.is_empty():
print("Stack is empty.")
else:
print("Stack elements:", self.stack[:self.top + 1])
stack = Stack()
stack.push(10)
stack.push(20)
stack.push(30)
print("栈顶元素:", stack.peek()) # 输出 30
print("栈大小:", stack.size()) # 输出 3
stack.pop(30) # 弹出 30
print("弹出后的栈顶元素:", stack.peek()) # 输出 204. Queues
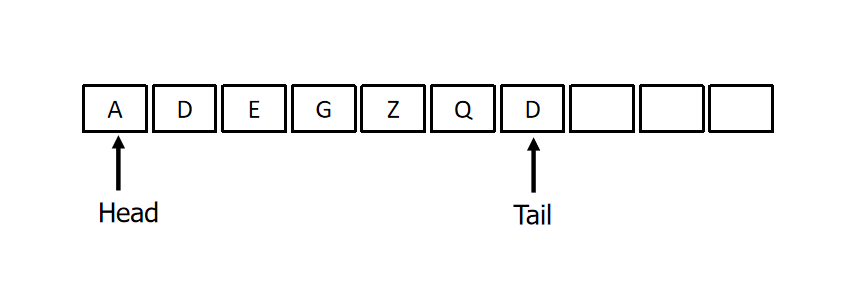
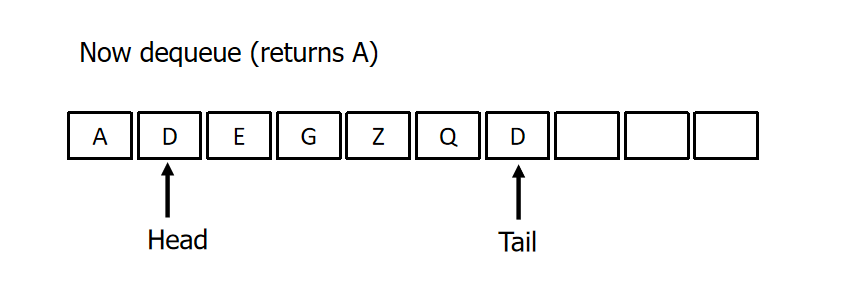
- Head and tail:
- A queue needs two pointers - one to point to the item at the start (head) of the queue, and one to point at the end tail
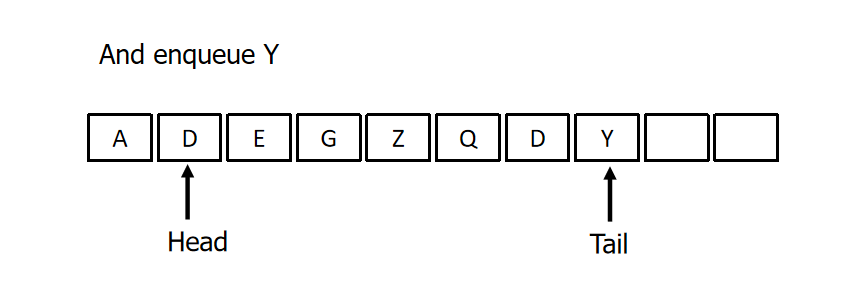
class CircularQueue:
def __init__(self, size):
self.queue = [None] * size
self.size = size
self.head = 0
self.tail = -1
def enqueue(self, node):
if (self.tail + 1) % self.size == self.head and self.queue[self.head] is not None:
print("queue full")
return
self.tail = (self.tail + 1) % self.size
self.queue[self.tail] = node
def dequeue(self):
if self.head == (self.tail + 1) % self.size and self.queue[self.head] is None:
print("queue is empty")
return
value = self.queue[self.head]
self.queue[self.head] = None
self.head = (self.head + 1) % self.size
return value
def display(self):
print("Queue:", self.queue)
print(f"Head at index {self.head}, Tail at index {self.tail}")
q = CircularQueue(8)
q.enqueue('A')
q.enqueue('D')
q.enqueue('E')
q.enqueue('G')
q.enqueue('Z')
q.enqueue('Q')
q.enqueue('D')
q.enqueue('Y')
q.display() # 输出队列内容及指针位置
print(q.dequeue()) # 输出:A
q.display()output
Queue: ['A', 'D', 'E', 'G', 'Z', 'Q', 'D', 'Y']
Head at index 0, Tail at index 7
A
Queue: [None, 'D', 'E', 'G', 'Z', 'Q', 'D', 'Y']
Head at index 1, Tail at index 75. Graphs
陌生英文单词:
- vertices: 顶点
- **incident:**附带的
- **adjacent = neighbours:**邻近的;靠近的
Items:
- undirected graph
- Vertex labelled graph:顶点标记图(顶点有属性,比如有颜色属性)
- Cyclic graph:有环图
- Acycic graph:无环图
- weighted graph:带权图(边带权)
- connected or unconnected graph:(非)连通图
- Adjacency Matrix:邻接矩阵
- Adjacency List:邻接表
5.1 图的添加、删除边和节点
class GraphAdjMatrix:
def __init__(self, vertices:list[int], edges: list[list[int]]):
self.vertices: list[int] = []
self.adj_mat: list[list[int]] = []
for val in vertices:
self.add_vertex(val)
for e in edges:
self.add_edge(e[0], e[1])
def size(self) -> int:
return len(self.vertices)
def add_vertex(self, val: int):
n = self.size()
self.vertices.append(val)
new_row = [0] * n
self.adj_mat.append(new_row)
for row in self.adj_mat:
row.append(0)
def remove_vertex(self, index: int):
if index >= self.size() or index < 0:
raise IndexError("Index out of the range")
self.vertices.pop(index)
self.adj_mat.pop(index)
for row in self.adj_mat:
row.pop(index)
def add_edge(self, i:int, j:int):
if i < 0 or j < 0 or i >= self.size() or j >= self.size():
raise IndexError("index out of the range")
if i == j:
raise ValueError("Edges from vertex to itself are not allowed.")
self.adj_mat[i][j] = 1
self.adj_mat[j][i] = 1
def remove_edge(self, i:int, j:int):
if i < 0 or j < 0 or i >= self.size() or j >= self.size():
raise IndexError("index out of the range")
if i == j:
raise ValueError("Deteling edge from vertex to itself is not allowed.")
self.adj_mat[i][j] = 0
self.adj_mat[j][i] = 0
def print(self):
print(f"vertices = ", self.vertices)
print("Adjacency Matrix = ")
self.print_matrix()
def print_matrix(self):
# 在顶点列表打印时,前面加一个空格
print(" " + " ".join(map(str, self.vertices)))
for i in range(self.size()):
self.adj_mat[i].insert(0, self.vertices[i])
for row in self.adj_mat:
print(" ".join(map(str, row)))
if __name__ == '__main__':
vertices = [1, 3, 2, 5, 4]
edges = [[0, 1], [0, 3], [1, 2], [2, 3], [2, 4], [3, 4]]
graph = GraphAdjMatrix(vertices, edges)
# graph.add_edge(0, 2)
# graph.remove_edge(0, 1)
# graph.add_vertex(6)
# graph.remove_vertex(1)
graph.print()5.2 DFS
def dfs_recursive(self, start: int, visited: list[bool]):
visited[start] = True
print(self.vertices[start], end=' ')
for neighbor, is_connected in enumerate(self.adj_mat[start]):
if is_connected and not visited[neighbor]:
self.dfs_recursive(neighbor, visited)
def dfs(self, start_vertex: int):
visited = [False] * self.size()
start_index = self.vertices.index(start_vertex)
self.dfs_recursive(start_index, visited)
print()测试代码:
def test_graph_adjmat_dfs():
print("=== 测试1:简单图 ===")
# 创建图
vertices = [0, 1, 2, 3, 4]
edges = [[0, 1], [0, 2], [1, 3], [2, 4]]
graph = GraphAdjMat(vertices, edges)
graph.print() # 打印邻接矩阵
print("DFS 从顶点 0 开始:")
graph.dfs(0) # 从顶点 0 开始进行 DFS 遍历,预期输出 0 1 3 2 4
print("\n=== 测试2:环形图 ===")
# 创建一个环形图
vertices = [0, 1, 2, 3]
edges = [[0, 1], [1, 2], [2, 3], [3, 0]]
graph = GraphAdjMat(vertices, edges)
graph.print() # 打印邻接矩阵
print("DFS 从顶点 0 开始:")
graph.dfs(0) # 从顶点 0 开始进行 DFS 遍历,预期输出 0 1 2 3
print("\n=== 测试3:不连通图 ===")
# 创建不连通的图
vertices = [0, 1, 2, 3, 4]
edges = [[0, 1], [2, 3]]
graph = GraphAdjMat(vertices, edges)
graph.print() # 打印邻接矩阵
print("DFS 从顶点 0 开始:")
graph.dfs(0) # 从顶点 0 开始进行 DFS 遍历,预期输出 0 1
print("DFS 从顶点 2 开始:")
graph.dfs(2) # 从顶点 2 开始进行 DFS 遍历,预期输出 2 3
print("\n=== 测试4:单一顶点 ===")
# 创建只有一个顶点的图
vertices = [0]
edges = []
graph = GraphAdjMat(vertices, edges)
graph.print() # 打印邻接矩阵
print("DFS 从顶点 0 开始:")
graph.dfs(0) # 从顶点 0 开始进行 DFS 遍历,预期输出 05.3 BFS
def bfs(self, start_vertex: int):
start_index = self.vertices.index(start_vertex)
queue = [start_index]
visited = [False] * self.size()
visited[start_index] = True
while queue:
vertex = queue.pop(0)
print(self.vertices[vertex], end=' ')
for neighbor, is_connected in enumerate(self.adj_mat[vertex]):
if not visited[neighbor] and is_connected:
visited[neighbor] = True
queue.append(neighbor)
print()