高级算法作业

School of Computing, Engineering and Mathematics (CEM)
Faculty of Engineering, Environment and Computing (EEC)
CUH500CMD ADVANCED ALGORITHMS | 2024
PORTFOLIO OF CODE | REPORT
NAME: Xiao XianYue
SID: 14553435
STD 1
1. pseudocode
SELECTION_SORT(A)
FOR i TO length(A)-1
min ← i
FOR j ← i + 1 TO length(A)
IF A[j] < A[min]
min ← j
SWAP (A, i, min)
RETURN A2. Two Solutions
Solution 1
def selection_sort(arr):
result = [] # Create a new list for storing the sorted list
for i in range(len(arr) - 1, 0, -1): # Iterate through the list from back to front
min = arr[i]
for j in range(i): # Iterate over all elements except i and find the minimum value
if arr[j] < min:
min = arr[j]
result.append(min) # Add the minimum value to the newly created list
arr.remove(min)
result.append(arr[0]) # Add the last remaining element to result(the list)
return result
print(selection_sort([5, 4, 3, 2, 1]))
Solution 2
def selection_sort(arr):
for i in range(len(arr)): # Iterate through the list from front to back
min_index = i
for j in range(i + 1, len(arr)): # Find the smallest value in an unsorted list
if arr[j] < arr[min_index]:
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i] # Swap the minimum value with i into the sorted list
return arr
print(selection_sort([5, 4, 3, 2, 1]))The one is written according to the pseudo-code above.

3. Explaining the code
Solution 1
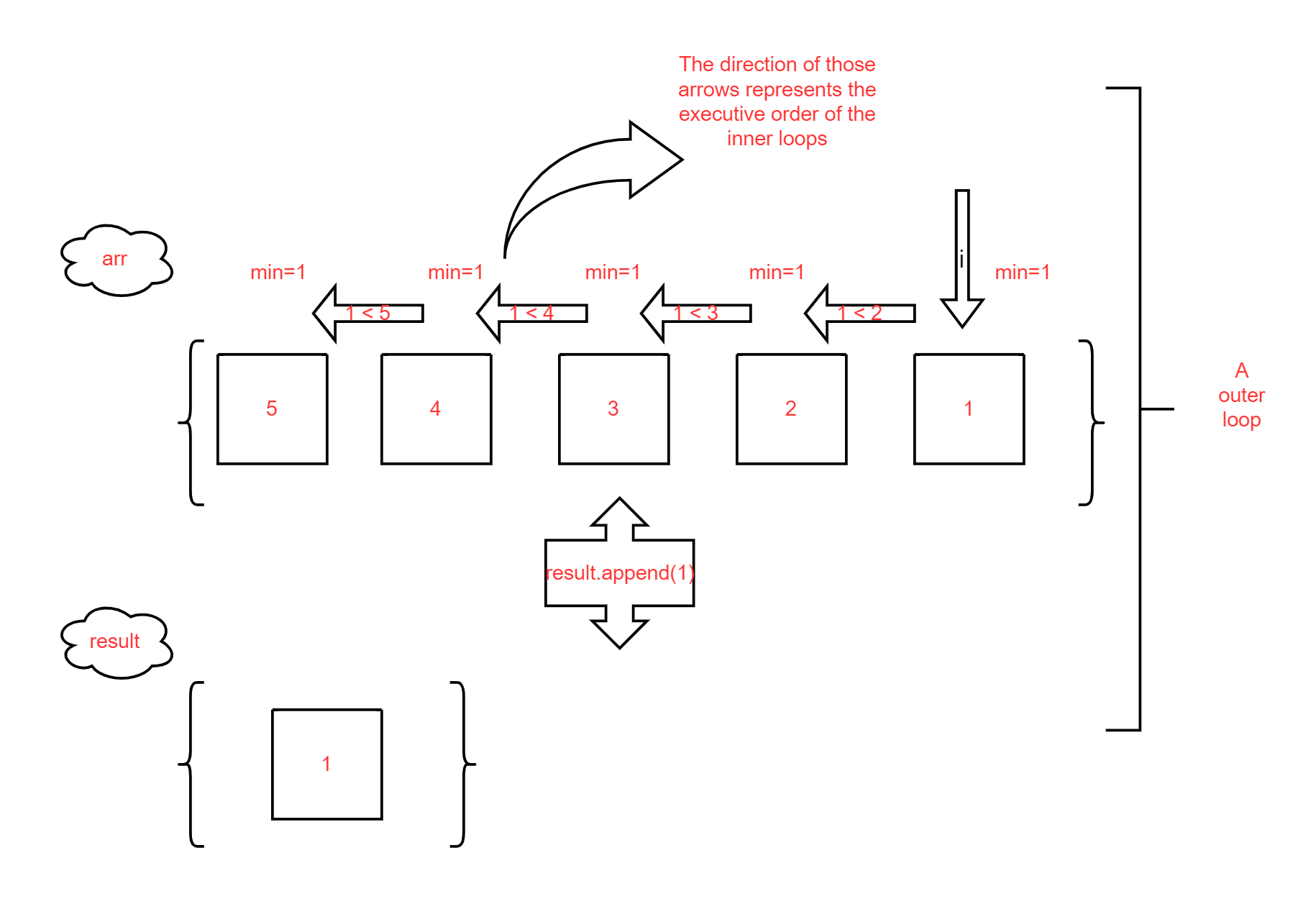
Firstly,
result = []: I create an empty listresultto store the final sorted elements. (adding elements one by one)Secondly, I use a outer loop:
for i in range(len(arr) - 1, 0, -1):. This loop processes the elements from back to front, accessing the last element of the unsorted list first.Thirdly,
min = arr[i]: I set a variableminthat is currently used to store the minimum value of the element value of the current unsorted list. Initialize this variable to the element at index i.Fourthly,
for j in range(i + 1, len(arr)):I use the inner loop to find the minimum elements in the unsorted list. As stated above, the inner loop is executed i times to compare the smallest value (which is stored asmin) in the unsorted list.if arr[j] < min: min = arr[j]Fifthly,
result.append(min)adds the minimum value to the end of a sorted list.Sixthly,
arr.remove(min). Remove the smallest value found from the original list to prevent the next iteration of the outerforloop from repeatedly adding the same smallest element, which has already been added toresult.After
len(arr) - 1times of outer loops, there is only one element left in the unsorted list, and this is the largest element, which is added to the very end of the sorted list.return the sorted list
result.Below is a schematic of the flow of the first outer loop.
Solution 2
This is code written according to the given pseudo-code, without having to create a new list and modify it directly on the original list.
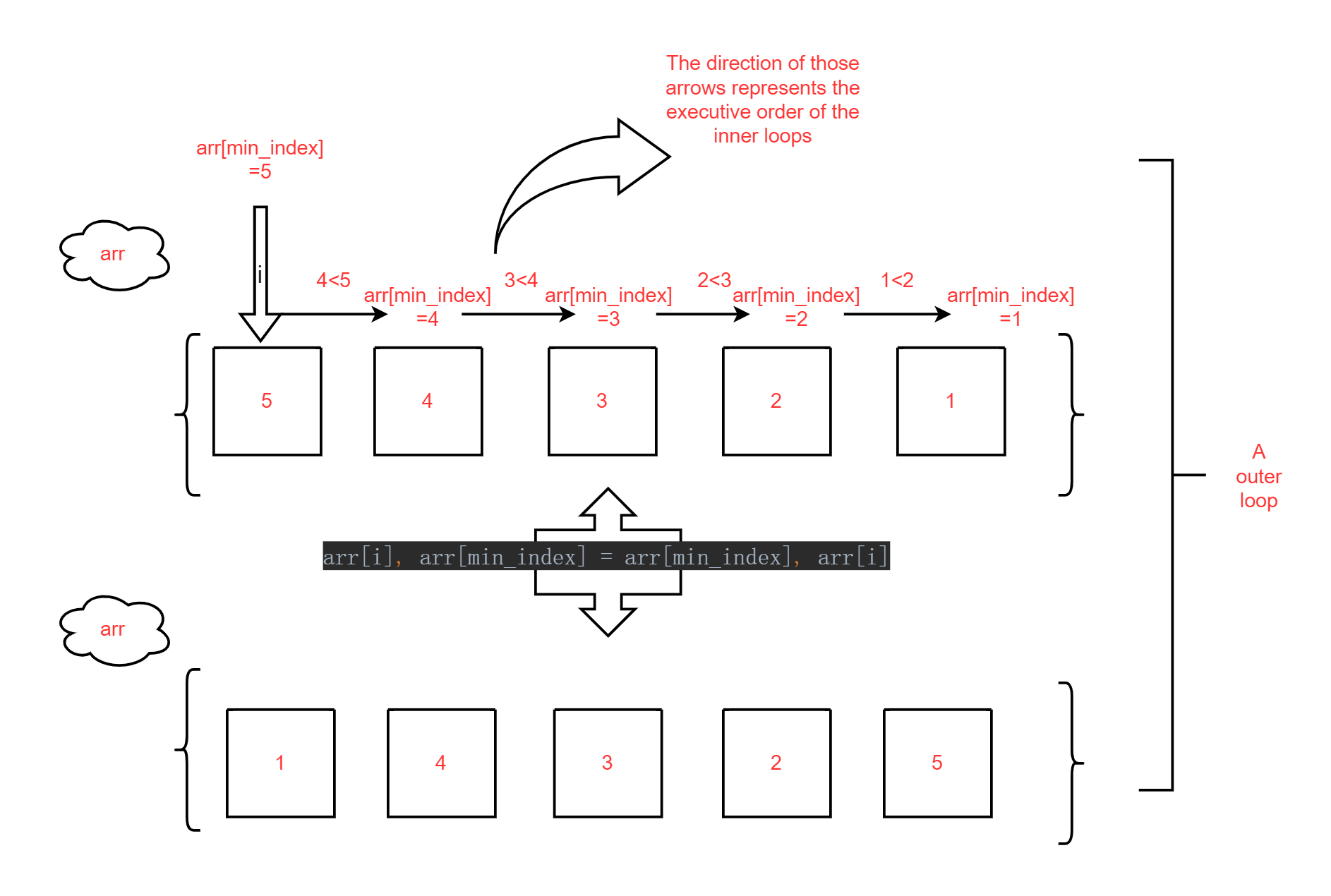
Firstly, Set up an outer loop that traverses the list from front to back.
Secondly, As in solution 1, create a variable
min_indexto store the minimum value of the current queue.Thirdly, Set up an inner loop that also compares
arr[i]one by one with the other elements in the list and finds the smallest one.Find the minimum value and swap places with
arr[i]. This is why the outer loop needs to be traversed from front to back. Because the smaller element has to be placed earlier in the queue.Returns the modified original list
arr.The flow chart below shows how the list changes after the first outer loop.
4. Evaluating the code
We try to evaluate both codes in terms of readability and conciseness.
Readability and conciseness
Solution 1:
for i in range(len(arr) - 1, 0, -1):The order of traversal of the outer loop: back-to-front traversal is a bit uncommon and can be confusing. Generally the selection ordering is traversed from front to back, which is more in line with most people's understanding.
arr.remove(min)The
removemethod: each time the minimum value is removed it changes the structure of the array, which may not make it easy to understand and may affect efficiency. Removing elements adds complexity to the code.min = arr[i]Actually, it's not good to use
minas a variable name!minis a built-in function in Python, which is confusing to the reader.
Solution 2:
- The traversal order of the outer loop: traversing from front to back is consistent with how people normally do things in order and is easy to understand.
for i in range(len(arr))- The code is simple and easy to read. There are no complex delete operations or extra data structures. It follows the basic logic of selective sorting and clearly expresses each step of the operation。
arr[i], arr[min_index] = arr[min_index], arr[i]We try to evaluate both codes in terms of complexity
Complexity
Solution 1:
Time Complexity:
- Outer loop:
for i in range(len(arr) - 1, 0, -1)This loop traverses the array from back to front, n-1 times, where n is the length of the array. - Inner loop:
for j in range(i)This loop iterates through the array from 0 to i-1. In the worst case, the inner loop will be executed at most n times (wheni = n-1). - remove(min): Each time
arr.remove(min)is called to remove the minimum value, the Python list's remove method needs to scan the entire array to find the element and remove it, with time complexity - Combined time complexity:
- Outer loop:
Space complexity:
Solution 2:
Space complexity: there is no other storage space
Time Complexity:
outer loop:
for i in range(len(arr))This loop traverses the entire arrayntimes.inner loop:
for j in range(i + 1, len(arr))This loop iterates fromi+1ton-1one at a time, and in the worst case the time complexity of the inner loop is O(n²). 3. swap operation: Swapping elements is a constant time operation O(n²).Swap operation: Swapping elements is a constant time operation O(1).
combined time complexity: the total time complexity of the outer and inner loops is O(n²), so the time complexity of the algorithm is
Overall Solution 2 is less complex than Solution 1.
STD 2
1. Code
Iterative
class TreeNode:
"""Binary Tree Node Classes"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None # Initial binary tree
def find_i(self, val):
cur = self.root # nodes in a binary tree
while cur: # If you don't know how many loops there could be, a while loop is appropriate.
if cur.val > val: # If the node is larger than the search value, the search value is in the left subtree of the node
cur = cur.left
elif cur.val < val: # If the node is smaller than the search value, the search value is in the right subtree of the node
cur = cur.right
else: # is equal to the search value, the loop ends
return True
return False
if __name__ == '__main__':
# Create a binary search tree manually
bst = BST()
bst.root = TreeNode(4)
bst.root.left = TreeNode(2)
bst.root.right = TreeNode(6)
bst.root.left.left = TreeNode(1)
bst.root.left.right = TreeNode(3)
bst.root.right.left = TreeNode(5)
bst.root.right.right = TreeNode(7)
# Test
print(bst.find_i(7)) # Expected output: True
print(bst.find_i(20)) # Expected output: False
print(bst.find_i(4)) # Expected output: True
print(bst.find_i(100)) # Expected output: False
print(bst.find_i(6)) # Expected output: True
print(bst.find_i(2)) # Expected output: True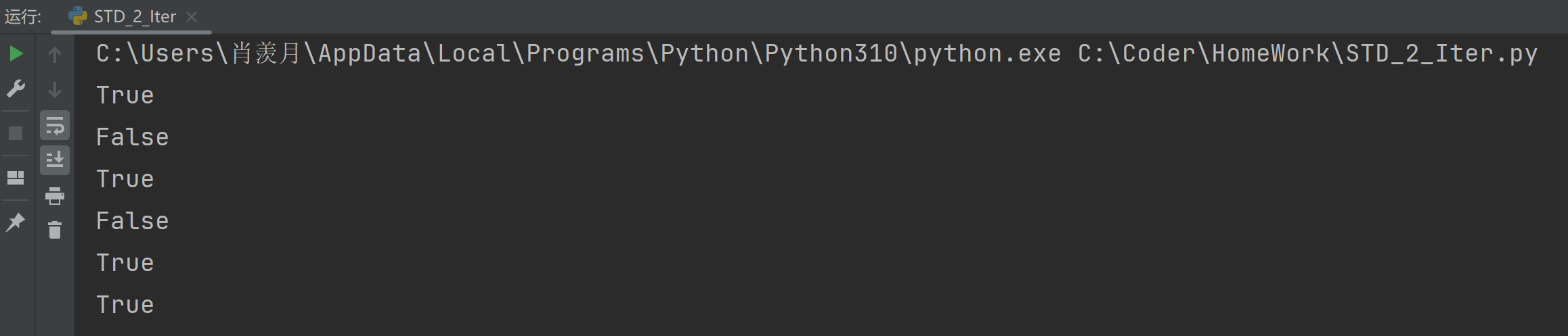
Recursive
class TreeNode:
"""Binary Tree Node Classes"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None # Initial binary tree
def find_r(self,target):
"""
Recursively searches for the target in the BST.
Returns True if found, False if not found, None if invalid input or empty tree.
"""
if self.root:
if self.find_r_helper(target, self.root): # if find_r_helper return True
return True
return False # # if find_r_helper return False
else:
return None
def find_r_helper(self,target,root):
if root is None:
return False
if target > root.val and root.right:
return self.find_r_helper(target,root.right) # Search in the right subtree
elif target < root.val and root.left:
return self.find_r_helper(target,root.left) # Search in the left subtree
if target == root.val:
return True
if __name__ == '__main__':
# Create a binary search tree manually
bst = BST()
bst.root = TreeNode(4)
bst.root.left = TreeNode(2)
bst.root.right = TreeNode(6)
bst.root.left.left = TreeNode(1)
bst.root.left.right = TreeNode(3)
bst.root.right.left = TreeNode(5)
bst.root.right.right = TreeNode(7)
# Test
print(bst.find_r(4)) # Expected: True
print(bst.find_r(9)) # Expected: False
print(bst.find_r(6)) # Expected: True
print(bst.find_r(0)) # Expected: False
print(bst.find_r(3)) # Expected: True
print(bst.find_r(7)) # Expected: True
print(bst.find_r(5)) # Expected: True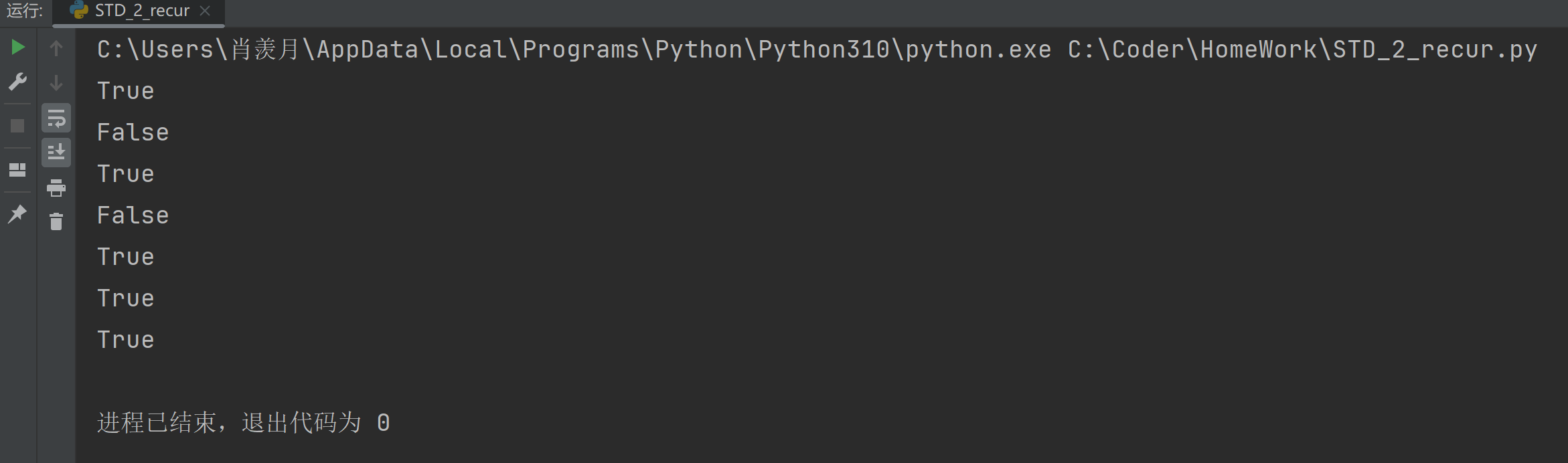
2. Explaining the code
Iterative
class TreeNode:
"""Binary Tree Node Classes"""
def __init__(self, val):
self.val = val
self.left = None
self.right = NoneHere I use a class to simulate the attribute of nodes in a binary tree. Assigning values to each node and setting the left and right subtrees of each node.
class BST:
def __init__(self):
self.root = None # Initial binary treeCreate a class that operates on binary trees. Initialise this binary tree to be empty. It is worth noting that the code all uses the root node of the binary tree to represent the entire binary tree.
def find_i(self, val):
cur = self.root # nodes in a binary treeUse a function to implement the search function to increase the modularity of the code and ease of calling. Create the variable cur initialised to the root node of the binary tree. This means that the following code will traverse the binary tree beginning with the root node. val is the value of the node we need to find.
while cur: # If you don't know how many loops there could be, a while loop is appropriate.
if cur.val > val: # If the node is larger than the search value, the search value is in the left subtree of the node
cur = cur.left
elif cur.val < val: # If the node is smaller than the search value, the search value is in the right subtree of the node
cur = cur.right
else: # is equal to the search value, the loop ends
return True
return FalseI use a while loop to traverse the binary tree because I don't know how many times we have to do the loop. If I knew exactly how many times the loop was going to be executed, a for loop would be more appropriate.
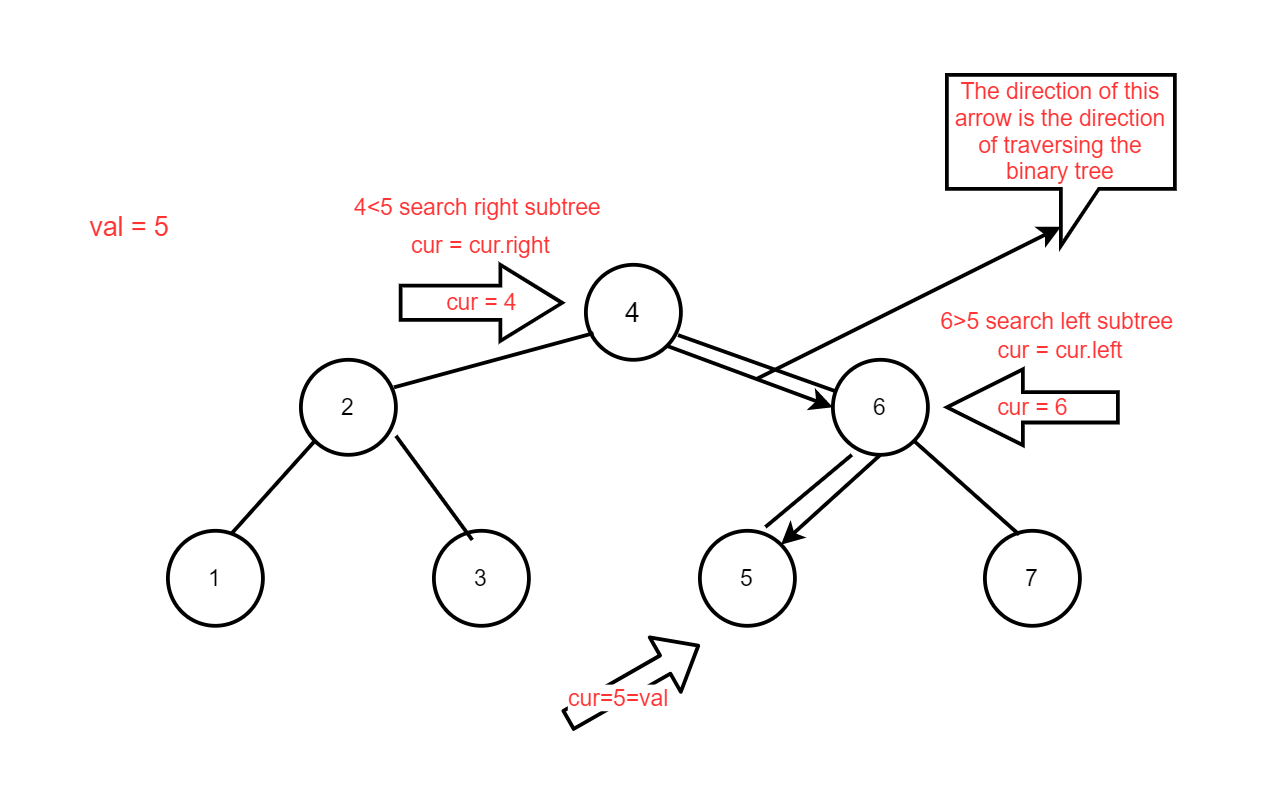
If
valis less than the current node value, it means thatvalexists in the left subtree of the current node. Ifvalis greater than the current node value, it means thatvalexists in the right subtree of the current node.Until a node with the same value as
valis found, return True and the function ends.If while loop ends (
curnode is empty, binary tree nodes are all traversed) no corresponding node is found, there is no node in the binary tree with the value val. Returns False.
if __name__ == '__main__':
# Create a binary search tree manually
bst = BST()
bst.root = TreeNode(4)
bst.root.left = TreeNode(2)
bst.root.right = TreeNode(6)
bst.root.left.left = TreeNode(1)
bst.root.left.right = TreeNode(3)
bst.root.right.left = TreeNode(5)
bst.root.right.right = TreeNode(7)
# Test
print(bst.find_r(4)) # Expected: True
print(bst.find_r(9)) # Expected: False
print(bst.find_r(6)) # Expected: True
print(bst.find_r(0)) # Expected: False
print(bst.find_r(3)) # Expected: True
print(bst.find_r(7)) # Expected: True
print(bst.find_r(5)) # Expected: TrueManually create a binary tree for searching.
Recursive
Only the following codes are different from Iterative, the logic of all other codes are exactly the same, you can refer to the description above.
def find_r(self,target):
"""
Recursively searches for the target in the BST.
Returns True if found, False if not found, None if invalid input or empty tree.
"""
if self.root:
if self.find_r_helper(target, self.root): # if find_r_helper return True
return True
return False # # if find_r_helper return False
else:
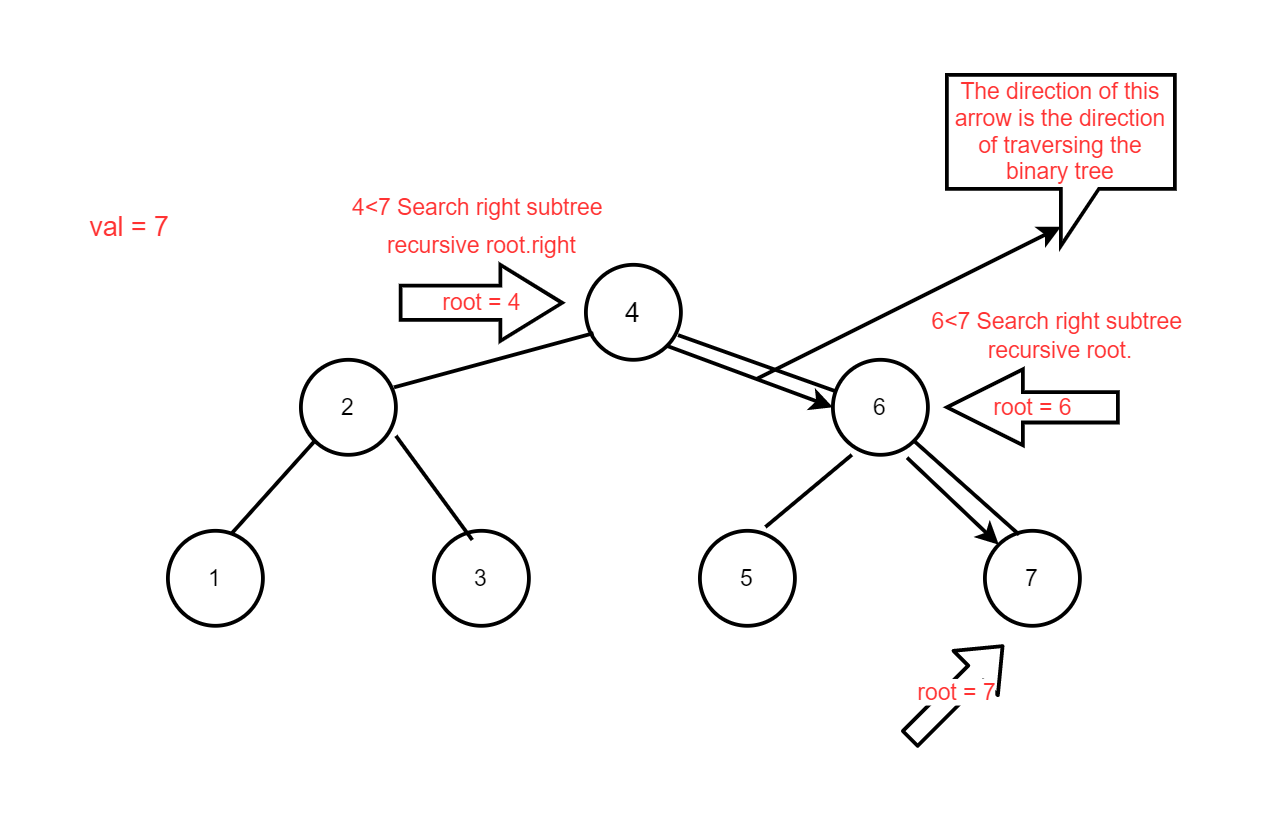
return None- Create a recursive find function,
find_r. - If the tree exists, check if
find_r_helperfinds the corresponding node value. - If it does, return True
- If it does, True. If it doesn't, False.
- If the tree does not exist, return False
def find_r_helper(self,target,root):
if root is None:
return False
if target > root.val and root.right:
return self.find_r_helper(target,root.right) # Search in the right subtree
elif target < root.val and root.left:
return self.find_r_helper(target,root.left) # Search in the left subtree
if target == root.val:
return True- Creates a function to find the value of a node
find_r_helper. - If the incoming tree is empty, return False.
- If the node value is less than the find value, recursively search its right subtree.
- If the node value is greater than the lookup value, recursively search the left subtree.
- If at this level of recursion the node value is equal to the find value, return True and pass it back one level at a time, with
find_r_helperreturning True at the end.
3. Evaluating the code
We try to evaluate both codes in terms of complexity
Time Complexity:
The time complexity of both solutions is
Space Complexity:
- Iterative: Only a pointer
curis used to point to the current node, no recursive call stack is needed. - Recursive: Since the depth of the recursion is the most significant source of space consumption, the space complexity is mainly determined by the maximum depth of the recursion.
- Worst Space Complexity: If the tree degenerates to a chained list (i.e., the height of the tree is
n), then the maximum depth of the recursion isnand the space complexity is - Best space complexity: if the tree is balanced (i.e., the height of the tree is
log n), then the maximum depth of the recursion islog nand the space complexity is
- Worst Space Complexity: If the tree degenerates to a chained list (i.e., the height of the tree is
- Iterative: Only a pointer
To summary, Recursive has a higher space complexity, especially when dealing with trees of greater depth which can lead to StackOverflow. Iterative code is not as elegant as Recursive but has a low space complexity.
STD 3
1. Code
class GraphAdjMat:
"Classes of undirected graphs based on adjacency matrix implementation"
def __init__(self, vertices: list[int], edges: list[list[int]]):
"""Vertex list, stores the vertex values in the graph, the element represents the “vertex value” and the index represents the “vertex index”."""
self.vertices: list[int] = []
"""Adjacency matrix, a two-dimensional list representing the connections between vertices of a graph, with row and column indices corresponding to “vertex indices”."""
self.adj_mat: list[list[int]] = []
# Iterate over the incoming vertex values and add them in order to the vertex list
for val in vertices:
self.add_vertex(val)
# Iterate through the list of incoming edges, adding them in turn to the adjacency matrix
for e in edges:
self.add_edge(e[0], e[1])
def size(self) -> int:
return len(self.vertices)
def add_vertex(self, val: int):
n = self.size()
self.vertices.append(val)
new_row = [0] * (n + 1)
self.adj_mat.append(new_row)
for row in self.adj_mat[:-1]:
row.append(0)
def remove_vertex(self, index: int):
# Check if the index is out of bounds and throw an exception if it is
if index >= self.size() or index < 0:
raise IndexError(f"Index {index} is out of range.")
self.vertices.pop(index)
self.adj_mat.pop(index)
# Remove the corresponding column from the adjacency matrix, removing the connection of this vertex to other vertices
for row in self.adj_mat:
row.pop(index)
def edge_num(self):
edge_count = 0
for row in self.adj_mat:
for edge in row:
if edge == 1:
edge_count += 1
return edge_count
def add_edge(self, i: int, j: int):
edge_number = self.edge_num()
# Check if i or j is out pf bounds and throe an exception if it is
if i >= self.size() or i < 0 or j >= self.size() or i >= self.size():
raise IndexError(f"index {i} or {j} is out of range.")
if i == j:
raise ValueError(f"Cannot add edge {i} to itself.")
self.adj_mat[i][j] = 1
self.adj_mat[j][i] = 1
if self.edge_num() - edge_number == 1:
return
else:
return False
def remove_edge(self, i: int, j: int):
edge_number = self.edge_num()
if i >= self.size() or i < 0 or j >= self.size() or i >= self.size():
raise IndexError(f"index {i} or {j} is out of range.")
if i == j:
raise ValueError(f"Cannot add edge {i} to itself.")
self.adj_mat[i][j] = 0
self.adj_mat[j][i] = 0
if edge_number - self.edge_num() == 1:
return
else:
return False
def print_matrix(self):
n = self.size()
print(" " + " ".join(map(str, range(n))))
print("index" + "-" * (4 * n - 1))
for i, row in enumerate(self.adj_mat):
print(f"{i} |" + " ".join(map(str, row)))
def print(self):
print("Vertex list = ", self.vertices)
print("adjacency matrix = ")
self.print_matrix()
if __name__ == "__main__":
# Initialize the undirected graph
vertices = [1, 3, 2, 5, 4]
edges = [[0, 1], [0, 3], [1, 2], [2, 3], [2, 4], [3, 4]]
graph = GraphAdjMat(vertices, edges)
graph.remove_edge(0,1)
graph.print()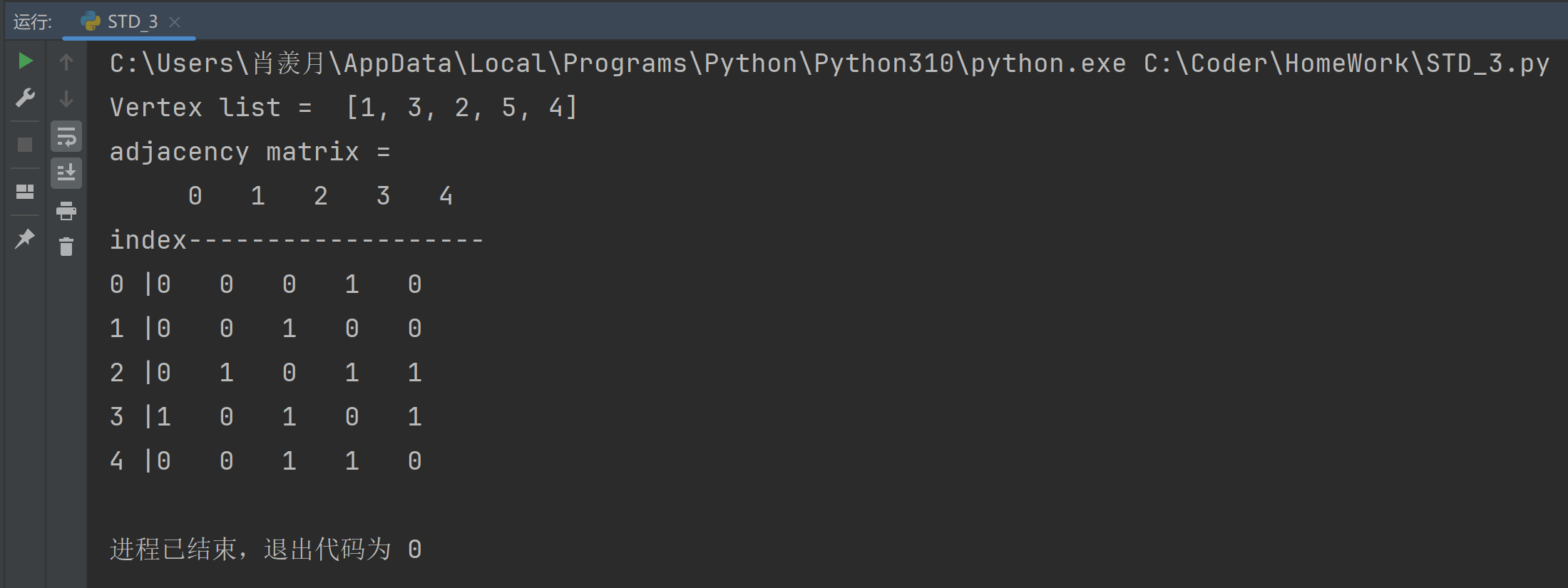
2. Explaining the Code
class GraphAdjMat:
def __init__(self, vertices: list[int], edges: list[list[int]]):
self.vertices: list[int] = []
self.adj_mat: list[list[int]] = []
for val in vertices:
self.add_vertex(val)
for e in edges:
self.add_edge(e[0], e[1])vertices for vertex; adj_mat is the adjacency matrix of the graph.
def size(self) -> int:
return len(self.vertices)View the current number of vertices of the graph.
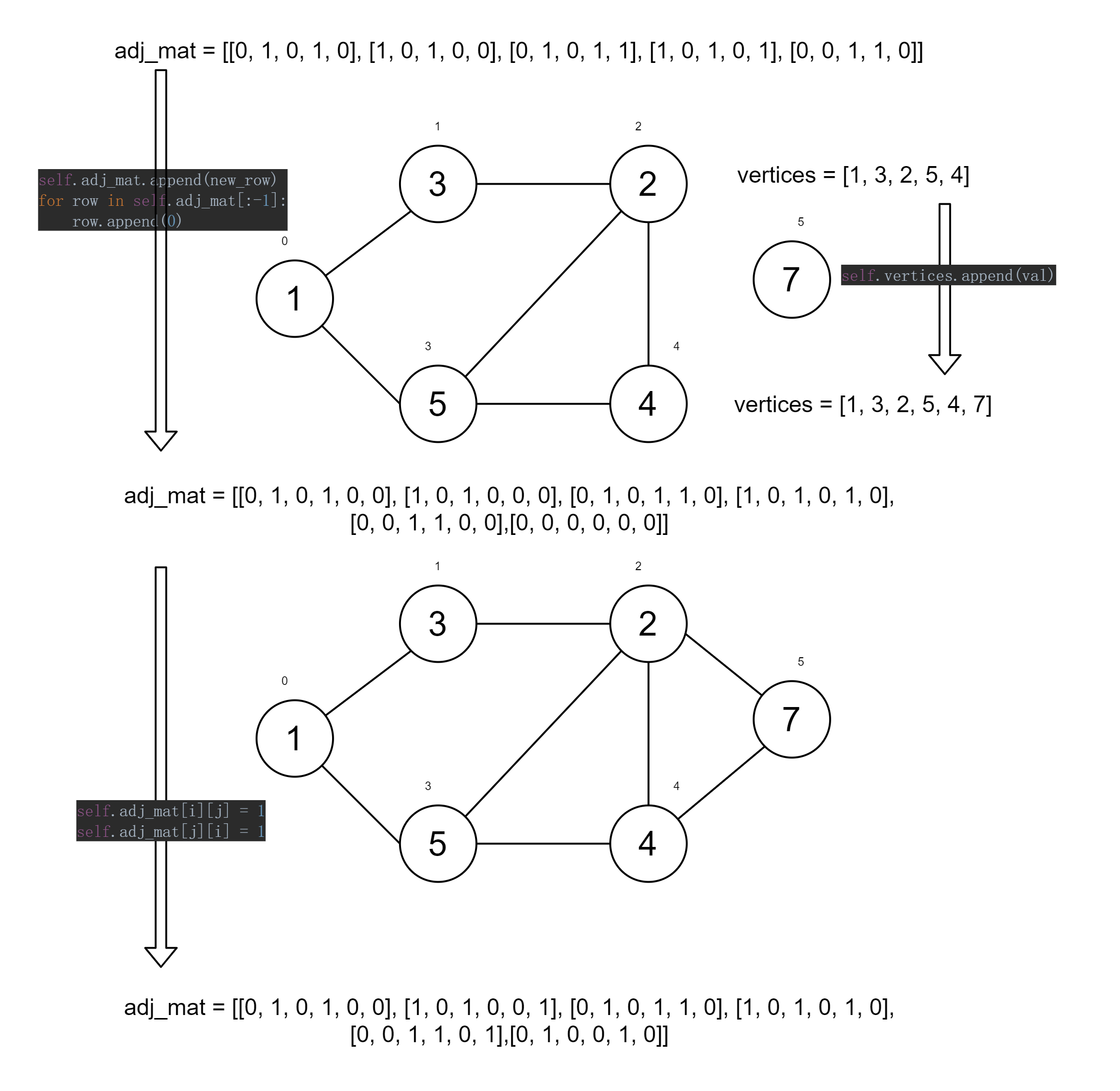
def add_vertex(self, val: int):
n = self.size()
self.vertices.append(val)
new_row = [0] * (n + 1)
self.adj_mat.append(new_row)
for row in self.adj_mat[:-1]:
row.append(0)- To add a node to the graph:
- First, get the current number of vertices
n. - Add the new node value to the
verticeslist. - Create a new row for the adjacency matrix with
n + 1zeros, representing no edges for the new node. - Append this new row to the adjacency matrix
adj_mat. - For all existing rows (except the new one), append a
0to indicate no connection to the new node.
- First, get the current number of vertices
def remove_vertex(self, index: int):
if index >= self.size() or index < 0:
raise IndexError(f"Index {index} is out of range.")
self.vertices.pop(index)
self.adj_mat.pop(index)
for row in self.adj_mat:
row.pop(index)- To remove a node from the graph:
- Check if the index is valid; if it's out of bounds (less than 0 or greater than the list length), raise an exception.
- Remove the vertex at the given index from the
verticeslist and the corresponding row from theadj_mat. - Iterate through the
adj_matand remove the element at the given index from each row.
def edge_num(self):
edge_count = 0
for row in self.adj_mat:
for edge in row:
if edge == 1:
edge_count += 1
return edge_countIterate over all elements of the edge list that have a value of 1 and store them in edge_count, which is the number of edges in the current graph.
def add_edge(self, i: int, j: int):
edge_number = self.edge_num()
# Check if i or j is out pf bounds and throe an exception if it is
if i >= self.size() or i < 0 or j >= self.size() or i >= self.size():
raise IndexError(f"index {i} or {j} is out of range.")
if i == j:
raise ValueError(f"Cannot add edge {i} to itself.")
self.adj_mat[i][j] = 1
self.adj_mat[j][i] = 1
if self.edge_num() - edge_number == 1:
return
else:
return FalseFirst, it checks if the vertex index is out of range or less than 0, and throws an exception if it is. Also, a vertex cannot add an edge pointing from itself to itself, otherwise an exception is thrown. Then, set adj_mat[i][j] and adj_mat[j][i] to 1 in the adjacency matrix to indicate that an undirected edge is added. Finally, check if the number of added edges is increased by 1, if yes, the addition is successful, otherwise return False.
def remove_edge(self, i: int, j: int):
edge_number = self.edge_num()
if i >= self.size() or i < 0 or j >= self.size() or i >= self.size():
raise IndexError(f"index {i} or {j} is out of range.")
if i == j:
raise ValueError(f"Cannot add edge {i} to itself.")
self.adj_mat[i][j] = 0
self.adj_mat[j][i] = 0
if edge_number - self.edge_num() == 1:
return
else:
return FalseSame logic as adding edges above.
def print_matrix(self):
n = self.size()
print(" " + " ".join(map(str, range(n))))
print("index" + "-" * (4 * n - 1))
for i, row in enumerate(self.adj_mat):
print(f"{i} |" + " ".join(map(str, row)))
def print(self):
print("Vertex list = ", self.vertices)
print("adjacency matrix = ")
self.print_matrix()print_matrix:
- First, get the number of vertices (n), which will define the size of the matrix.
- Next, print the column headers (vertex indices) from 0 to (n-1), making sure each is aligned with 3 spaces for clarity.
- Add a dividing line to separate the headers from the actual matrix data.
- Then, go through the adjacency matrix row by row. Each row shows the connections for a specific vertex:
- Start with the row number on the left, followed by the connection status for each column:
- Use 1 to show there's an edge.
- Use 0 if there's no edge.
- Start with the row number on the left, followed by the connection status for each column:
3. Visualise some code
Initialised to the graph below, with the vertex list and edge list labelled in it.
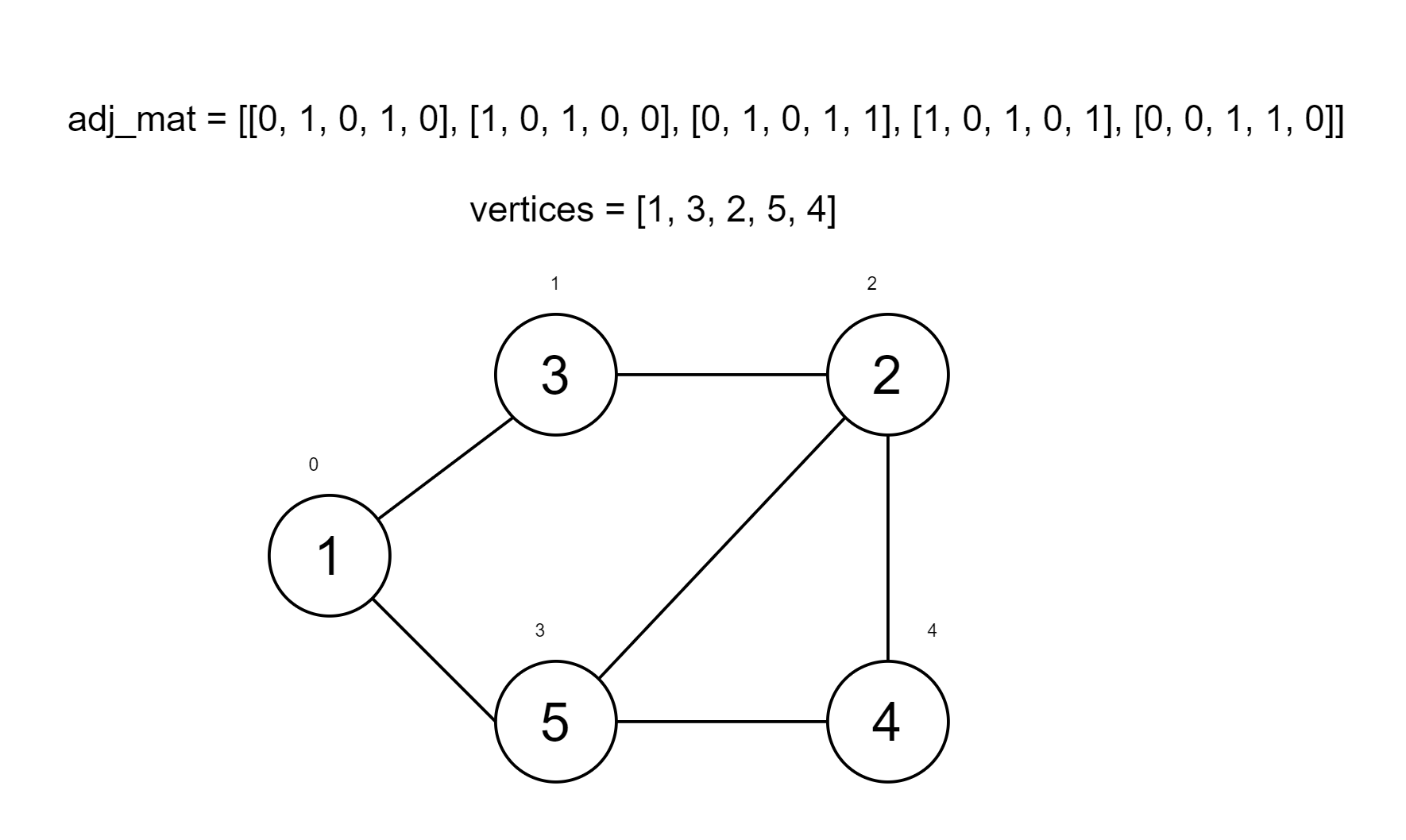
Try adding a vertex with a value of 7 and add edges 2-7; 4-7.
4. Evaluating the code
We try to evaluate both codes in terms of Modularity and reusability.
- Modularity
- Each function is split into separate methods like
add_vertex,add_edge,remove_vertex, andprint_matrix, which makes the code easy to follow and work with. It's pretty straightforward to understand what each method does. - The methods are short and focused, which makes them easier to debug and keeps the overall structure neat.
- Each function is split into separate methods like
- Reusability
- The way the logic is written for adding and removing vertices and edges makes it flexible enough to use in different types of graph implementations.
- Using an adjacency matrix works well for undirected graphs, but it might need some tweaks if you want to handle directed or weighted graphs.
GOOD MODULARITY AND REUSABILITY!
We try to evaluate both codes in terms of Efficiency
for val in vertices:
self.add_vertex(val)
for e in edges:
self.add_edge(e[0], e[1])- Using a for loop to add nodes and edges each time the class is initialized would be a slow operation when dealing with large graphs.
def add_vertex(self, val: int):
n = self.size()
self.vertices.append(val)
new_row = [0] * (n + 1)
self.adj_mat.append(new_row)
for row in self.adj_mat[:-1]:
row.append(0)- And count the number of vertices
self.sizeevery time you call the functions that add vertices and add edges. Wouldn't it be better to just count the number of vertices when initializing?
def remove_vertex(self, index: int):
if index >= self.size() or index < 0:
raise IndexError(f"Index {index} is out of range.")
self.vertices.pop(index)
self.adj_mat.pop(index)
for row in self.adj_mat:
row.pop(index)- After deleting the vertices, each row of the entire adjacency matrix must be traversed to delete the elements column by column, which is also a less time-efficient (as
POOR EFFICIENCY!!
ADV 1
1. Code
class Node:
def __init__(self, data=None):
self.data = data
self.left = None
self.right = None
class BinaryTree:
def __init__(self):
self.root = None
def insert(self, data):
if self.root is None:
self.root = Node(data)
else:
self._insert(data, self.root)
def _insert(self, data, cur_node):
if data < cur_node.data:
if cur_node.left is None:
cur_node.left = Node(data)
else:
self._insert(data, cur_node.left)
elif data > cur_node.data:
if cur_node.right is None:
cur_node.right = Node(data)
else:
self._insert(data, cur_node.right)
else:
print("Value already present in tree")
def display(self, cur_node):
lines, _, _, _ = self._display(cur_node)
for line in lines:
print(line)
def _display(self, cur_node):
if cur_node.right is None and cur_node.left is None:
line = '%s' % cur_node.data
width = len(line)
height = 1
middle = width // 2
return [line], width, height, middle
if cur_node.right is None:
lines, n, p, x = self._display(cur_node.left)
s = '%s' % cur_node.data
u = len(s)
first_line = (x + 1) * ' ' + (n - x - 1) * '_' + s
second_line = x * ' ' + '/' + (n - x - 1 + u) * ' '
shifted_lines = [line + u * ' ' for line in lines]
return [first_line, second_line] + shifted_lines, n + u, p + 2, n + u // 2
if cur_node.left is None:
lines, n, p, x = self._display(cur_node.right)
s = '%s' % cur_node.data
u = len(s)
first_line = s + x * '_' + (n - x) * ' '
second_line = (u + x) * ' ' + '\\' + (n - x - 1) * ' '
shifted_lines = [u * ' ' + line for line in lines]
return [first_line, second_line] + shifted_lines, n + u, p + 2, u // 2
left, n, p, x = self._display(cur_node.left)
right, m, q, y = self._display(cur_node.right)
s = '%s' % cur_node.data
u = len(s)
first_line = (x + 1) * ' ' + (n - x - 1) * '_' + s + y * '_' + (m - y) * ' '
second_line = x * ' ' + '/' + (n - x - 1 + u + y) * ' ' + '\\' + (m - y - 1) * ' '
if p < q:
left += [n * ' '] * (q - p)
elif q < p:
right += [m * ' '] * (p - q)
zipped_lines = zip(left, right)
lines = [first_line, second_line] + [a + u * ' ' + b for a, b in zipped_lines]
return lines, n + m + u, max(p, q) + 2, n + u // 2
def remove(self, target):
if self.root is None: # If the tree is empty
return False
elif self.root.data == target: # If the root node is the target
if self.root.left is None or self.root.right is None:
# If the root has one or no child, replace the root with its child
self.root = self.root.left or self.root.right
else:
# If the root has two children, handle it separately
self.root = self._delete_node_with_two_children(self.root)
return True
else:
# If the root is not the target, find and delete the target
cur, parent = self.root, None
while cur and cur.data != target:
parent = cur
if target < cur.data:
cur = cur.left
else:
cur = cur.right
if cur is None: # If the target is not found
return False
if cur.left is None or cur.right is None:
# If the node has one or no child, replace it with its child
child = cur.left or cur.right
if cur.data < parent.data:
parent.left = child
else:
parent.right = child
else:
# If the node has two children, handle it separately
self._delete_node_with_two_children(cur)
return True
def _delete_node_with_two_children(self, node):
# Find the smallest node in the right subtree
pre, re_node = node, node.right
while re_node.left:
pre = re_node
re_node = re_node.left
# Replace the target node's value with the smallest node's value
node.data = re_node.data
# Remove the smallest node
if re_node.right:
if pre.left == re_node:
pre.left = re_node.right
else:
pre.right = re_node.right
else:
if pre.left == re_node:
pre.left = None
else:
pre.right = None
return node
# Example calls, which construct and display the tree
bst = BinaryTree()
bst.insert(4)
bst.insert(2)
bst.insert(6)
bst.insert(1)
bst.insert(3)
bst.insert(5)
bst.insert(7)
bst.insert(8)
print("Before removing root (4):")
bst.display(bst.root)
bst.remove(4)
print("\nAfter removing root (4):")
bst.display(bst.root)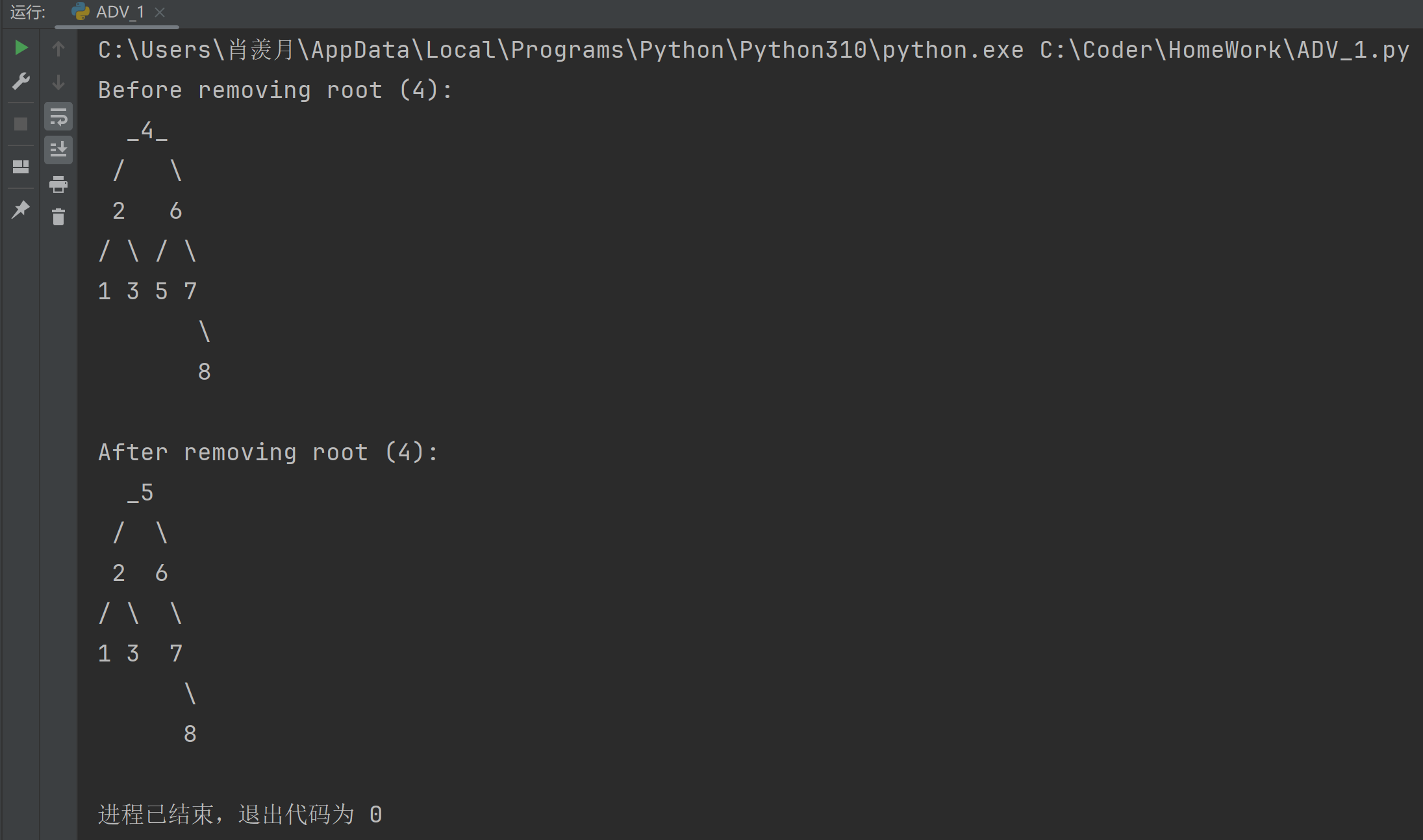
2. Explaining the Code
Only the remove function and the if_left_and_right function are discussed here. The rest of the functions are code given in Aula.
def remove(self, target):
if self.root is None:
return Falseif self.root is None, indicates that the binary tree is empty and returns it directly.
elif self.root.data == target:
if self.root.left is None or self.root.right is None:
root_child = self.root.left or self.root.right
self.root = root_child
else:
self.root = self.i_delete_node_with_two_children(self.root)
return TrueIf the value of the root node in the given tree just equals target:
- If the left and right child nodes of the root node are both empty, or both are null:
- Set
root_childto store the only child node that exists for the root node (e.g., if the right child exists,root_childequals the right child; if the left child exists,root_childequals the left child. If neither child exists,root_childwill be null). - Remove the root node and directly replace the original binary tree with
root_childas the root node.
- Set
- If both the left and right child nodes of the root exist:
- Perform operations using the
if_left_and_rightfunction. This is because I want to follow the code flow sequentially, and explanations for functions will appear later in the text.
- Perform operations using the
- Returns
Truefor successful deletion.
else:
cur, parent = self.root, None
while cur and cur.data != target:
parent = cur
if target < parent.data:
cur = cur.left
elif target > parent.data:
cur = cur.rightIf the value of the root node in the binary tree being traversed does not equal target:
- Use
curto store the currently traversed node, and useparentto store the node that was traversed beforecur, i.e., the parent node ofcur. - The
whileloop continues traversing the binary tree. As long ascuris not null and does not equaltarget, the loop proceeds. - In the first step of the loop, assign
parent = cur, storing the node obtained in the previouswhileiteration inparent. - If
target < parent.data, traverse the left subtree of the current node. Iftarget > parent.data, traverse the right subtree of the current node.
if cur is None:
return
if cur.left is None or cur.right is None:
child = cur.right or cur.left
if cur.data < parent.data:
parent.left = child
else:
parent.right = child
else:
self._delete_node_with_two_children(cur)
return TrueAfter the while loop, the node cur with value target and its parent parent have been found:
The logic of this part of the code is the same as in the first step dealing with the root node. You can refer to the explanation of the first step.
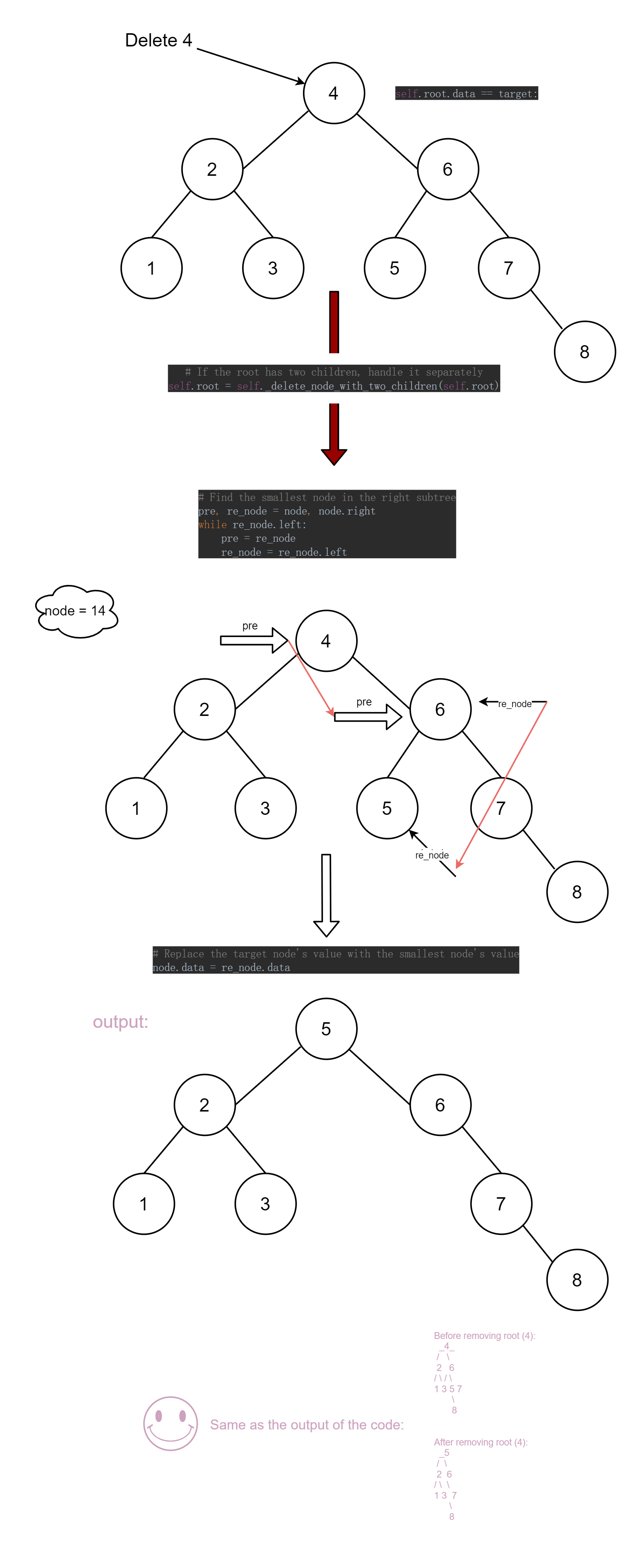
def _delete_node_with_two_children(self, node):
pre, re_node = node, node.right
while re_node.left:
pre = re_node
re_node = re_node.left
node.data = re_node.data
if re_node.right:
if pre.left == re_node:
pre.left = re_node.right
else:
pre.right = re_node.right
else:
if pre.left == re_node:
pre.left = None
else:
pre.right = None
return nodeThis function handles the case when the node to be deleted has both left and right children. It replaces the node with the smallest value in the right subtree.
- Input:
node(the node to be deleted). - Set
re_nodeto the right child of the target node to find the smallest node in the right subtree. Also, store its parent aspre. - Use a
whileloop to find the smallest node by moving left through the tree.prekeeps track of the parent ofre_node. - Once the smallest node is found, its value replaces the value of the node to be deleted.
If re_node has a right child:
- If
re_nodeis a left child of its parent, update the parent's left pointer tore_node.right. - If
re_nodeis a right child of its parent, update the parent's right pointer tore_node.right.
If re_node has no children:
- If
re_nodeis a left child, set the parent's left pointer toNone. - If
re_nodeis a right child, set the parent's right pointer toNone.
3. Visualise the code (steps)
4. Evaluating the code
Efficiency Evaluation
- Redundancy in Traversal: The code redundantly checks the left and right children of the node both in
removeand in the helper function_delete_node_with_two_children. For example:- In
remove, we check ifcur.leftorcur.rightisNoneto determine if the node has one or no children. - Then, in
_delete_node_with_two_children, we check again to remove the in-order successor node.
- In
- Space Complexity: The space complexity is
- Time Complexity: The time complexity is
his the height of the tree. In a balanced BST, this is
Quality Evaluation
Function and Variable Names:
- Function names like
removeand_delete_node_with_two_childrenare clear but could be made more descriptive. For example,_delete_node_with_two_childrencould be renamed todelete_with_two_childrenfor better readability. - Variable names such as
cur,parent, andchildare standard, butcurcould be renamed tocurrent_nodefor better clarity. Similarly,preandre_nodeshould be renamed toparentandsuccessor.
- Function names like
Input Validation: The code lacks input validation. For instance, there’s no check for invalid input like a
Nonevalue fortarget. Input validation could be added to ensure robustness.Code Structure
- Redundancy: There are redundant checks for nodes with one or no children. These could be refactored into a separate helper function.
- The logic in
_delete_node_with_two_childrenis functional but could be simplified or split into smaller functions for clarity.
ADV 3
1. Code
import concurrent.futures # Used for implementing concurrency
import newspaper # Used for scraping articles from news websites
from newspaper import Article # Used for processing individual articles
import timeit # Used for measuring execution time
# Non-concurrent version: Sequentially fetch headlines from each URL
def get_headlines():
# Define the list of URLs to scrape
URLs = [
'http://www.foxnews.com/',
'http://www.cnn.com/',
'http://www.derspiegel.de/',
'http://www.bbc.co.uk/',
'https://theguardian.com',
]
# Iterate through each URL
for url in URLs:
# Build a newspaper source object using newspaper.build
result = newspaper.build(url, memoize_articles=False)
print(f'\nThe headlines from {url} are:\n') # Print the current URL
# Fetch the first 5 articles
for i in range(5): # Ensure a maximum of 5 articles are fetched
try:
art = result.articles[i] # Get the i-th article
art.download() # Download article content
art.parse() # Parse article content
print(art.title) # Print the article title
except IndexError:
# Handle cases where the website has fewer than 5 articles
print(f"Less than 5 articles available on {url}")
break
# Concurrent version: Use a thread pool to concurrently fetch headlines from multiple URLs
def get_headlines_concurrently():
# Define the list of URLs to scrape
URLs = [
'http://www.foxnews.com/',
'http://www.cnn.com/',
'http://www.derspiegel.de/',
'http://www.bbc.co.uk/',
'https://theguardian.com',
]
# Define a function to fetch the top 5 headlines from a single URL
def fetch_headlines(url):
try:
# Build a newspaper source object using newspaper.build
result = newspaper.build(url, memoize_articles=False)
headlines = [] # Store the list of headlines for the current URL
# Fetch the first 5 articles
for i in range(5): # Ensure a maximum of 5 articles are fetched
try:
art = result.articles[i] # Get the i-th article
art.download() # Download article content
art.parse() # Parse article content
headlines.append(art.title) # Add the title to the list
except IndexError:
# Exit the loop if there are fewer than 5 articles
break
return url, headlines # Return the URL and the list of headlines
except Exception as e:
# Handle exceptions during the scraping process
return url, [f"Error fetching articles: {e}"]
# Create a thread pool using ThreadPoolExecutor
with concurrent.futures.ThreadPoolExecutor() as executor:
# Submit all tasks to the thread pool
future_to_url = {executor.submit(fetch_headlines, url): url for url in URLs}
# Retrieve results for each task
for future in concurrent.futures.as_completed(future_to_url):
url, headlines = future.result() # Get the result (URL and list of headlines)
print(f'\nThe headlines from {url} are:\n') # Print the current URL
for headline in headlines: # Iterate through and print the list of headlines
print(headline)
# Test the performance of the non-concurrent and concurrent versions
if __name__ == '__main__':
# Measure the average execution time of the non-concurrent version
non_concurrent_time = timeit.timeit(
"get_headlines()", # Code to execute
setup="from __main__ import get_headlines", # Setup the execution environment
number=2 # Run the code 2 times
) / 2 # Calculate the average time
print(f"Non-concurrent version average time: {non_concurrent_time:.2f} seconds")
# Measure the average execution time of the concurrent version
concurrent_time = timeit.timeit(
"get_headlines_concurrently()", # Code to execute
setup="from __main__ import get_headlines_concurrently", # Setup the execution environment
number=2 # Run the code 2 times
) / 2 # Calculate the average time
print(f"Concurrent version average time: {concurrent_time:.2f} seconds")Test outcome is in “Explaining the Code”
2. Explaining the Code
- Import the required libraries.
import concurrent.futures
import newspaper
from newspaper import Article
import timeit- Non-concurrent version
def get_headlines():
URLs = [
'http://www.foxnews.com/',
'http://www.cnn.com/',
'http://www.derspiegel.de/',
'http://www.bbc.co.uk/',
'https://theguardian.com',
]
for url in URLs:
result = newspaper.build(url, memoize_articles=False)
print(f'\nThe headlines from {url} are:\n')
for i in range(5):
try:
art = result.articles[i]
art.download()
art.parse()
print(art.title)
except IndexError:
print(f"Less than 5 articles available on {url}")
break- URL List: Defines a list of 5 news website URLs as the crawling targets.
- Traverse each
url. Use the variableresultto store a news source object created withnewspaper.build. - For the first 5 articles (indices 0-4), call the
download()andparse()methods to download and parse the article content. - Print the extracted titles.
- Exception Handling: If the target website has fewer than 5 articles, catch an
IndexErrorand print a warning message. Thistry...exceptblock was added to prevent issues like network errors or other problems from affecting the data retrieval process.
- Concurrent version.
def get_headlines_concurrently():
URLs = [
'http://www.foxnews.com/',
'http://www.cnn.com/',
'http://www.derspiegel.de/',
'http://www.bbc.co.uk/',
'https://theguardian.com',
]
def fetch_headlines(url):
try:
result = newspaper.build(url, memoize_articles=False)
headlines = []
for i in range(5):
try:
art = result.articles[i]
art.download()
art.parse()
headlines.append(art.title)
except IndexError:
break
return url, headlines
except Exception as e:
return url, [f"Error fetching articles: {e}"]- This part of the logic is much the same as the non-concurrent version.
with concurrent.futures.ThreadPoolExecutor() as executor:
future_to_url = {executor.submit(fetch_headlines, url): url for url in URLs}
for future in concurrent.futures.as_completed(future_to_url):
url, headlines = future.result()
print(f'\nThe headlines from {url} are:\n')
for headline in headlines:
print(headline)- A thread pool (
ThreadPoolExecutor) is created to handle multiple URLs at the same time. - Tasks for fetching headlines are submitted to the pool using
executor.submit(). - As tasks are completed, their results (URL and headlines) are processed and printed. This allows for efficient parallel execution, reducing the overall runtime.
- Performance Comparison
if __name__ == '__main__':
non_concurrent_time = timeit.timeit("get_headlines()", setup="from __main__ import get_headlines", number=2) / 2
print(f"Non-concurrent version average time: {non_concurrent_time:.2f} seconds")
concurrent_time = timeit.timeit("get_headlines_concurrently()", setup="from __main__ import get_headlines_concurrently", number=2) / 2
print(f"Concurrent version average time: {concurrent_time:.2f} seconds")- Non-concurrent runtime, call
get_headlines(). - Concurrent runtime, call
get_headlines_concurrently(). - This step is done by calculating the average runtime of both codes. Below is the test output:
Non-concurrent version average time: 10.25 seconds
Concurrent version average time: 4.12 seconds- The non-concurrent version processes each URL serially, resulting in a total runtime that is the sum of each task's runtime.
- The concurrent version uses a thread pool to process multiple URLs in parallel, downloading and parsing articles at the same time, significantly reducing runtime.
- The performance advantage of concurrency is even more significant when the number of URLs is large or network latency is high.
3. Evaluating the Code
We try to evaluate both codes in terms of Quality.
- Advantages:
- The code accomplishes its goal by retrieving the top 5 news headlines from various websites using both non-concurrent and concurrent methods.
- The function and variable names are descriptive and easy to understand, such as
get_headlinesandfetch_headlines. - The code logic is reasonable and can handle common errors, such as insufficient articles on a website, through
try...exceptto catchIndexError.
- Disadvantages:
- Lack of input validation:
- The format of the URLs in the input list is not verified for validity.
- If an invalid URL is passed, the program might throw unhandled exceptions.
- Redundant code:
- The error-handling code inside the
fetch_headlinesfunction is slightly redundant, such as the two-layertry...exceptstructure (outer layer for URL fetching exceptions, inner layer for article index exceptions), which can be optimized.
- The error-handling code inside the
- Lack of input validation:
