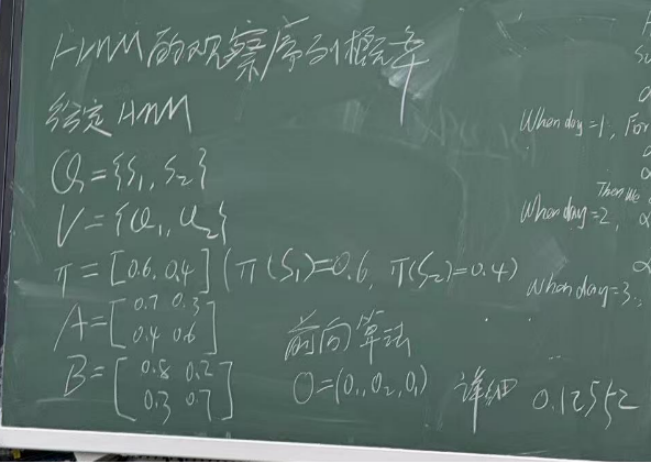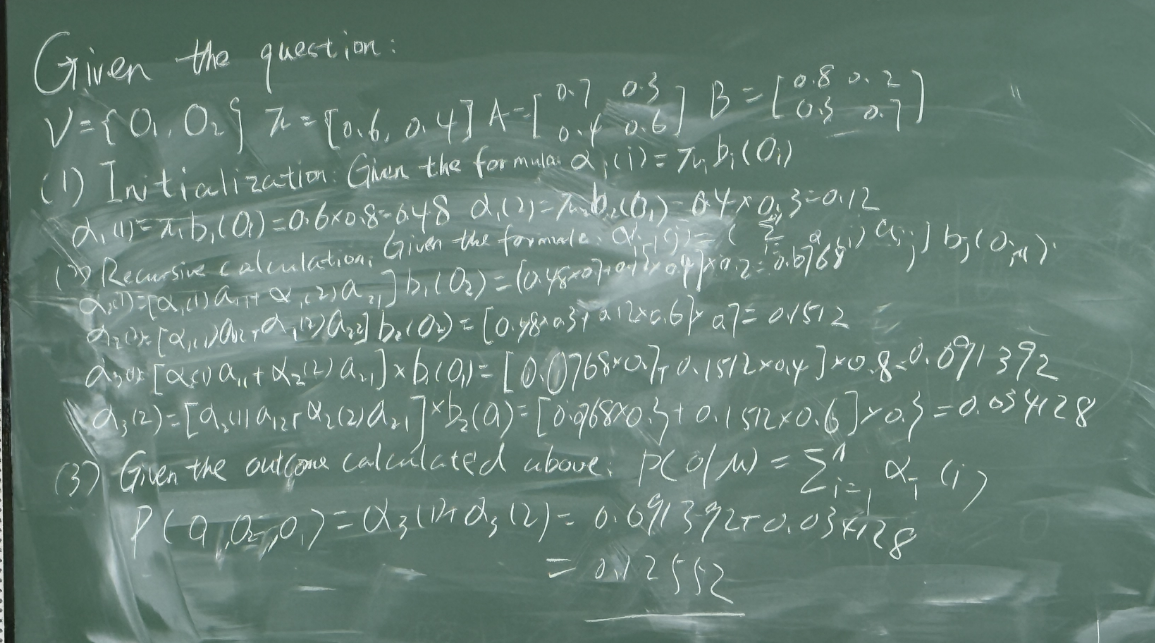图模型

XiaoXianYue原创2025年4月10日大约 8 分钟

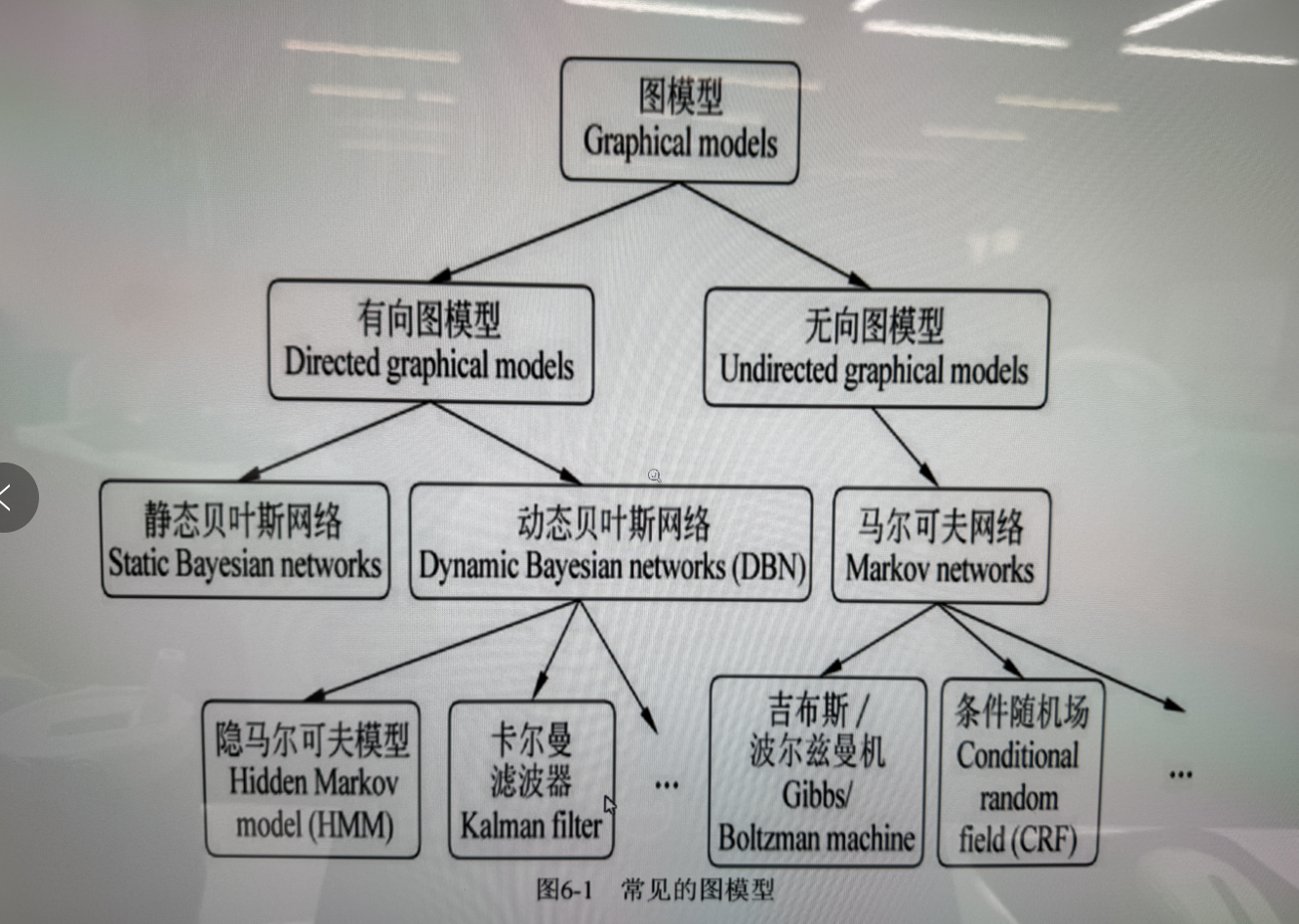
🌟 图模型（Graphical Models）总述：

图模型是一类用图结构来表示变量之间依赖关系的概率模型。

节点（Node）：代表随机变量
边（Edge）：表示变量之间的条件依赖关系

1️⃣ 有向图模型（Directed Graphical Models）

又称为贝叶斯网络（Bayesian Networks），边是有方向的，表示因果关系。

🔹 静态贝叶斯网络（Static Bayesian Networks）

原理：基于贝叶斯定理，用有向无环图（DAG）建模变量之间的依赖关系。
功能：推理、因果分析、预测
应用：医学诊断、金融风险评估、学生知识建模（如知识追踪）

🔹 动态贝叶斯网络（Dynamic Bayesian Networks, DBN）

原理：是静态贝叶斯网络在时间序列上的扩展，建模变量随时间的变化。
功能：时间序列预测、状态估计
应用：语音识别、运动轨迹分析、机器人定位

✅ 隐马尔可夫模型（Hidden Markov Model, HMM）
- 原理：假设系统的状态是隐藏的，只能通过观测变量间接观察。
- 功能：建模隐藏状态随时间变化的序列
- 应用：语音识别、文本标注（如词性标注）、生物序列分析
✅ 卡尔曼滤波器（Kalman Filter）
- 原理：用于线性系统的状态估计，假设噪声是高斯分布
- 功能：实时估计系统状态
- 应用：导航系统（如GPS）、飞行控制、目标跟踪

2️⃣ 无向图模型（Undirected Graphical Models）

又称马尔可夫网络（Markov Networks），边无方向，侧重表示联合概率分布。

🔹 马尔可夫网络（Markov Networks）

原理：使用图结构描述随机变量之间的对称依赖
功能：联合建模、能量函数建模
应用：图像分割、网络结构分析、自然语言处理中的结构预测

✅ 吉布斯/玻尔兹曼机（Gibbs/Boltzmann Machine）
- 原理：基于能量函数的无向网络，使用吉布斯采样进行学习
- 功能：建模高维联合分布，学习特征表示
- 应用：深度学习（早期深度置信网络的构成）、推荐系统
✅ 条件随机场（Conditional Random Field, CRF）
- 原理：在给定观测序列的条件下建模标签序列概率
- 功能：解决序列标注问题，考虑上下文依赖
- 应用：分词、词性标注、命名实体识别（NER）

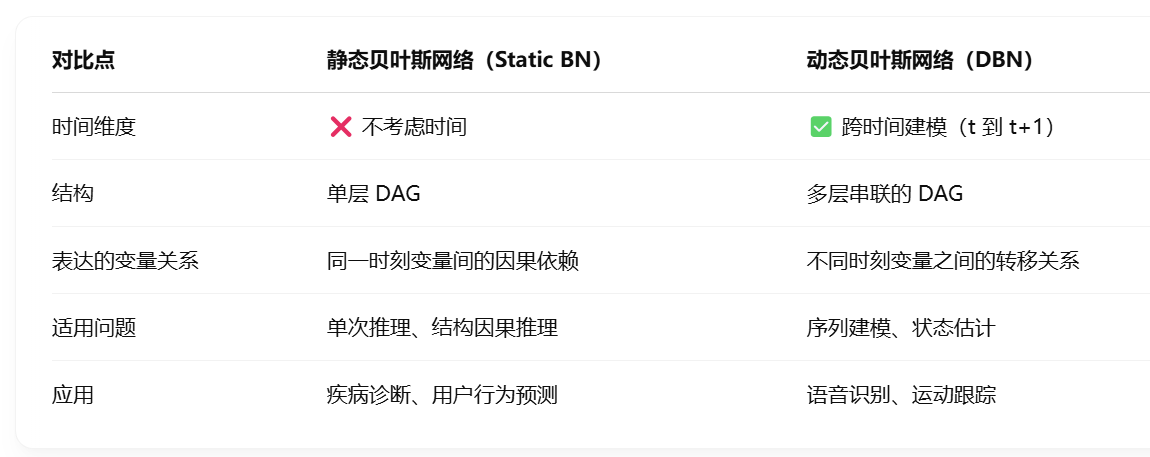
区别

生成式判别式本质区别是什么？优点是什么？典型的有哪些？

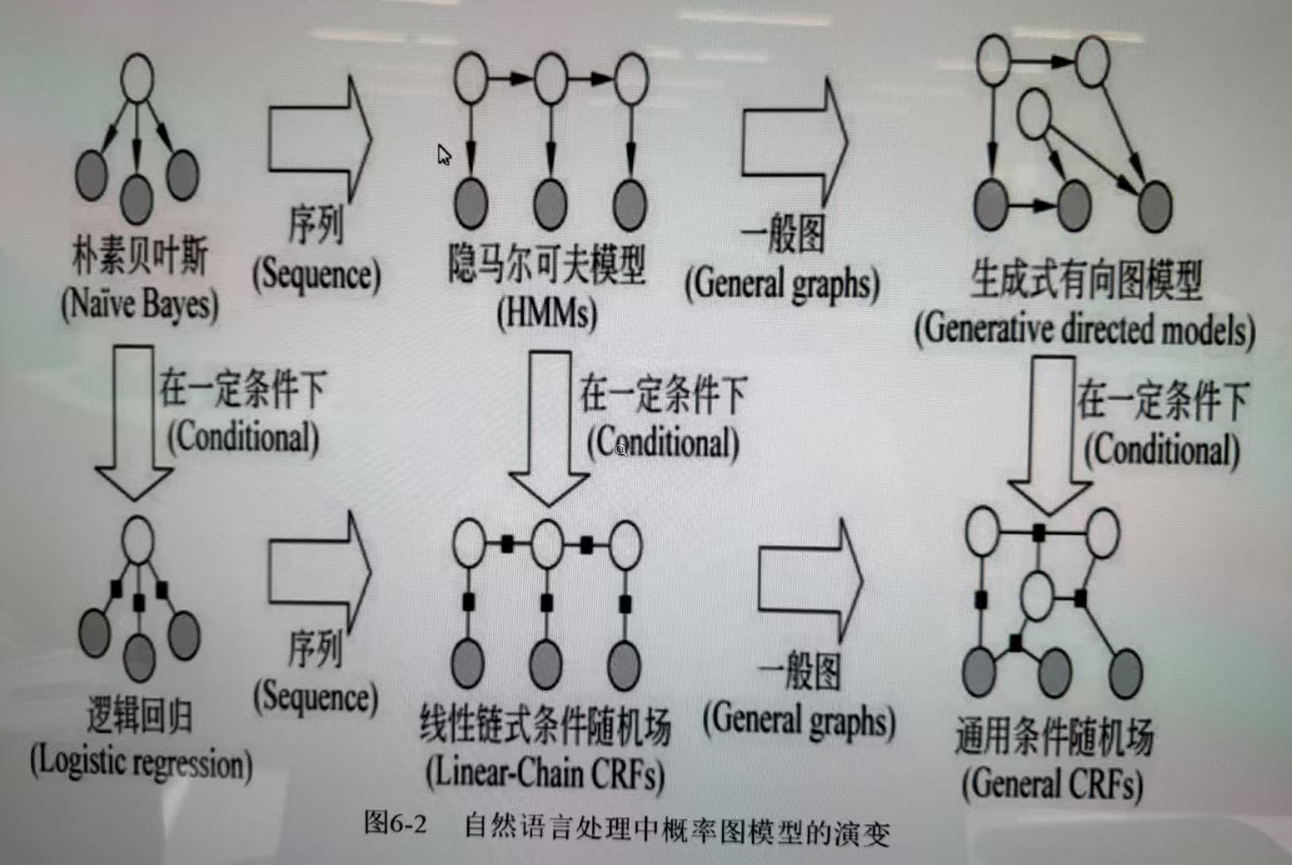
图片介绍

🧩 第一阶段：单变量独立假设 → 简单模型

朴素贝叶斯（Naive Bayes）

生成式模型：建模联合概率 P(x, y)
结构特征：输入特征之间相互独立（有向图）
缺点：忽略特征之间的依赖
应用：文本分类、垃圾邮件识别

⬇️ 加入“条件建模”思想

逻辑回归（Logistic Regression）

判别式模型：直接建模条件概率 P(y | x)
结构：扁平图（所有特征直接作用于标签）
优点：分类效果通常优于朴素贝叶斯
应用：情感分析、二分类任务等

🧩 第二阶段：引入“序列建模”能力

HMM（隐马尔可夫模型）

生成式：建模 P(x, y)，含有隐状态
结构：链式有向图（时间序列结构）
应用：语音识别、词性标注、机器翻译初期模型

⬇️ 加入条件建模

Linear-Chain CRF（线性链式条件随机#场）

判别式：建模 P(y | x)，同时考虑状态间和观测之间的依赖
改进点：克服 HMM 的独立假设（允许输入间任意依赖）
应用：中文分词、NER、语法分析等

🧩 第三阶段：从“序列模型”推广到“一般图结构”

Generative Directed Models（生成式有向图模型）

扩展：HMM 的结构变得更复杂，可任意有向图（如 DBN）
能力提升：表达更复杂的因果依赖
应用：动态系统建模、多变量因果分析

⬇️ 加入条件建模

General CRFs（通用条件随机场）

判别式：最强大的 CRF 表达形式
结构：图结构可以是任意的（如图像中的网格结构）
应用：图像分割、结构预测、多维依赖的 NLP 任务

贝叶斯网络

用于处理不确定性和不完整性问题
有向无环图
节点表示随机变量，有向边表示条件依赖关系。被指到的节点依存于指它的节点。

例题重要

✅ 使用贝叶斯公式：

我们要求：

P (N e w s = T ∣ H i s t o r y = T) = \frac{P (N e w s = T, H i s t o r y = T)}{P (H i s t o r y = T)}

所以我们要分别计算：

$P (N e w s = T, H i s t o r y = T)$
$P (H i s t o r y = T)$

✅ 步骤一：枚举所有 `News=T` 且 `History=T` 的情况

枚举 Sightseeing 的两种状态（T/F）：

N=T, S=T, H=T

P = P (N = T) \cdot P (S = T ∣ N = T) \cdot P (H = T ∣ S = T, N = T) = 0.2 \cdot 0.1 \cdot 0.4 = 0.008

N=T, S=F, H=T

P = 0.2 \cdot 0.9 \cdot 0.3 = 0.054

→ 所以：

P (N = T, H = T) = 0.008 + 0.054 = 0.062

✅ 步骤二：计算所有 `History=T` 的情况（枚举所有 N/S）

N=T, S=T, H=T：0.008 ✅
N=T, S=F, H=T：0.054 ✅
N=F, S=T, H=T：

P = 0.8 \cdot 0.4 \cdot 0.8 = 0.256

N=F, S=F, H=T：

P = 0.8 \cdot 0.6 \cdot 0.5 = 0.24

→ 所以：

P (H = T) = 0.008 + 0.054 + 0.256 + 0.24 = 0.558

✅ 最终代入贝叶斯公式：

P (N e w s = T ∣ H i s t o r y = T) = \frac{0.062}{0.558} \approx 0.1111

贝叶斯的表示，推断和学习

📌 一、表示（Representation）

贝叶斯网络是一种有向无环图（DAG），它用来表示变量之间的条件依赖关系。

包含两个核心部分：

结构（Structure）：
图中每个节点代表一个随机变量，边表示条件依赖关系。
比如 A → B 表示 B 条件依赖于 A。
参数（Parameters）：
每个变量都有一个条件概率分布（CPD）：
$P (X_{i} | Parents (X_{i}))$

所以整个网络表示的是：

P (X_{1}, X_{2}, . . ., X_{n}) = \prod_{i = 1}^{n} P (X_{i} | Parents (X_{i}))

📌 二、推断（Inference）

推断是指给定一部分变量的值（即证据），求其他变量的后验概率。

常见的推断任务：

边缘推断（Marginal Inference）：
计算某变量的边缘概率，比如 $P (A)$
条件推断（Conditional Inference）：
给定证据，求某个变量的条件概率，比如 $P (A | B = b)$
最可能解释（MAP）：
寻找使后验概率最大的变量赋值。

📌 三、学习（Learning）

学习是指从数据中构建贝叶斯网络，包括学习：

结构学习（Structure Learning）：
- 知道变量但不知道图的结构。
参数学习（Parameter Learning）：
- 已知图结构，估计每个节点的条件概率表（CPD）。

马尔科夫

📊 马尔科夫模型 vs 隐马尔科夫模型

比较维度	马尔科夫模型（MM）	隐马尔科夫模型（HMM）
📌 模型名称	Markov Model	Hidden Markov Model
🎯 状态是否可见	可见（Visible）	不可见（Hidden）（只能通过观测值间接得知）
👀 观测输出	无	有（每个隐状态生成一个观测值）
🔁 转移结构	显式状态转移（如 S1 → S2）	状态之间有转移，同时每个状态生成一个观测
🎲 建模对象	状态的序列概率： $P (S_{1}, S_{2}, . . ., S_{T})$	状态与观测的联合概率： $P (O_{1}, . . ., O_{T}, S_{1}, . . ., S_{T})$
📐 参数组成	状态转移概率矩阵	状态转移概率 + 发射概率（观测概率）
🧠 应用场景	简单随机过程建模（如棋盘移动）	语音识别、词性标注、分词、手写识别等
🧩 典型问题	状态转移分析	三大问题：评估（Evaluation）、解码（Decoding）、学习（Learning）
⛓️ 举例	天气转移模型（晴→阴→雨）	天气（隐状态）→ 温度/风力（观测值）