语言模型

1. 基本概念

1.1 文法

• n元文法（n-gram）模型

• 例子：

1.3 使用二元文法例子

image-20250331094603921

• 二元文法样本空间是 $N^2$
• 效果比一元文法强

2. 参数估计

重要！！！！！

示例讲解

image-20250331095009414

• $P(A|B)$
  • 分子的意思是：A 在 B 后面出现的次数，
  • 分母的意思是 B 后面出现任何词的次数。
  • 每个 P 表示 A 在 B 后面出现的概率。
  • 每个 P 相乘，得到了句子的概率。

3. 数据平滑

• 模型评估：困惑度和交叉熵越小越好。下面的图重要！！！！！

• 概念复习：
  • 训练语料(training data)：用于建立模型，确定模型参数的已知语料。
  • 最大似然估计(maximum likelihood Evaluation, MLE)：用相对频率计算概率的方法。
• 基本约束：

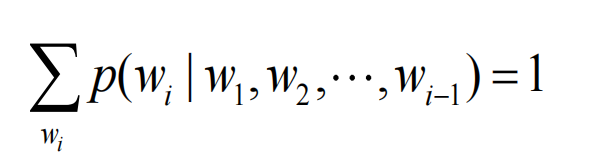
🔍 举个例子：

假设你输入了前两个词：“我 爱”，模型现在要预测下一个词 是什么。

可能的候选词和对应的条件概率：

候选词 条件概率
你 0.4
他 0.3
吃饭 0.2
其他词（若干） 加起来 0.1

这些概率的总和 必须是 1，否则模型就不是一个合法的概率模型。

3.1 应用示例

• 不能因为语料库中没有以 Cher 开头的句子就判别整个句子概率为 0，特别是语料库数据较少的时候，这种情况时常出现。

3.2 困惑度

• $W_T$：表示测试文本 $T$ 的总词数。
• $p(T)$：表示模型 $p$ 给出整个文本 $T$ 的概率，也就是所有词的联合概率 $p(w_1,w_2,...,w_{W_T})$。

相关信息

假设模型预测的概率如下（随便举个数字）：

• $p(w_1=\mathrm{我})=0.2$
• $p(w_2=\mathrm{喜}\mathrm{欢}|w_1=\mathrm{我})=0.5$
• $p(w_3=\mathrm{吃}|w_1,w_2)=0.3$
• $p(w_4=\mathrm{苹}\mathrm{果}|w_1,w_2,w_3)=0.1$

那么这个句子的联合概率就是：

$$p(T)=0.2\times 0.5\times 0.3\times 0.1=0.003$$

3.3 加一法

$$p(w_i|w_{i-1})=\frac{1+c(w_{i-1}{w}_i)}{|V|+\sum _{w_i}c(w_{i-1}{w}_i)}$$

• $|V|$：词汇表大小（不同词的总数）
• 分母中 $\sum c(w_{i-1}{w}_i)$：表示前一个词是 $w_{i-1}$ 时所有接续词的总出现次数

例子:

<BOS> John read Moby Dick <EOS>

<BOS> Mary read a different book <EOS>

<BOS> She read a book by Cher <EOS>

• 不加平滑：

  • $p(\text{Cher}|\text{<BOS>})=0/3=0$
  • $p(\text{read}|\text{Cher})=0/1=0$
    ——> 这样的话，整个句子的概率就会变成 0，因为乘法里有 0！

• 加一平滑后：

$$p(\text{Cher}|\text{<BOS>})=\frac{0+1}{11+3}=\frac{1}{14}$$

词汇量大小 $|V|=11$

$3$：<BOS> 出现了 3 次

考试出大题作答步骤要详细，根据ppt的步骤来

3.4 减值法/折扣法

填空要考

• Good-Turing Method: Reduces the observed counts of non-zero events according to a formula. The saved probability mass is evenly redistributed to zero-frequency events.

• Katz Back-off Method: Applies the Good-Turing method to compute discounted probabilities for non-zero events, and then allocates the remaining probability mass to zero-frequency events using lower-order distributions.

• Absolute Discounting: Subtracts a fixed amount from the count of each non-zero event, regardless of context. The saved probability mass is then evenly allocated to zero-frequency events.

• Linear Discounting: Reduces the count of each non-zero event proportionally based on its original frequency. The saved probability mass is then evenly distributed to zero-frequency events.

下面开始讲解四种减值法

3.4.1 GoodTurning