形式语言与自动机及其在NLP中的应用

1. 基本概念

• 树的概念（省略）

• 字符串（string）：

  • 定义：假定 $\Sigma$ 是字符的有限集合，由 中字符相连而成，不包括任何字符的字符串称为空串，记作 ε：Epsilon（艾普西龙） |ε|= 0
  • 全体字符：${\Sigma }^{\ast }$

• 闭包：

正则式：必考

1. XY：表示两个正规表达式 $X$ 和 $Y$ 的连接（concatenation），即先匹配 $X$ 再匹配 $Y$。例如，如果 $X=\{a,b\}$，$Y=\{c\}$，那么 $XY=\{ac,bc\}$。X·Y：同样表示连接，点号（·）是显式的连接符号，但一般可省略，因此 XY = X·Y。
2. 直观来说，X | Y 代表的是由 $X$ 或 $Y$ 生成的字符串集合中的任何一个。

3. U ∪ V：表示两个集合 $U$ 和 $V$ 的并集（union），即同时包含 $U$ 和 $V$ 的所有元素。

4. U·V：表示两个集合的连接，即对于集合 $U$ 中的每个字符串 $u$ 和 $V$ 中的每个字符串 $v$，形成 $uv$ 这样的新字符串，构成新集合。

例子

2. 形式语言

所有的语言都是：句子和符号[字符]串的有限或无限的集合

• 穷举法：只适合句子数目有限的语言
• 文法描述、语法描述：生成语言中合格的句子
• 自动机：对输入的句子进行检验，区别哪些是语言中的句子，哪些不是语言中的句子

2.1 定义 重点

image-20250313151132703

2.2 推导，派生定义

• 直接派生/推导：

• 间接派生：

2.3 最左/右推导

2.4 句子和句型

2.5 正则文法

2.6 上下文无关文法 必考

*例子 必考

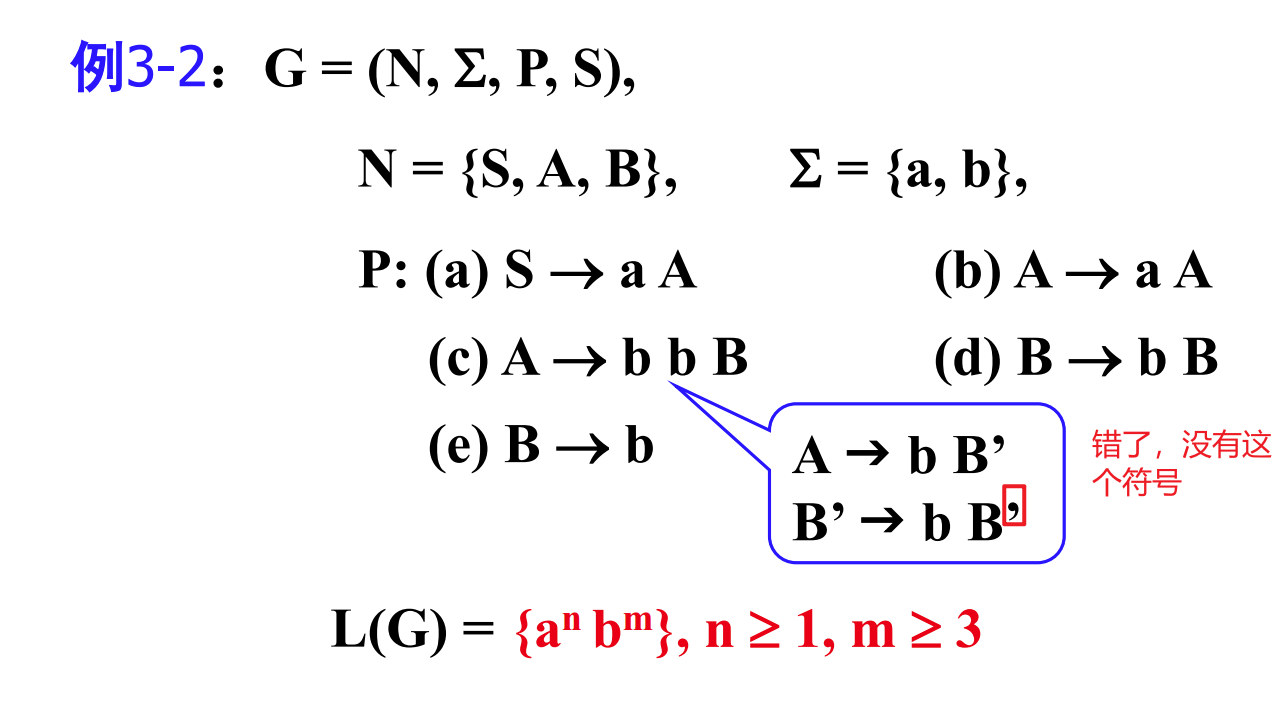
图中文法的讲解

图中的文法 $G$ 定义如下：

• 非终结符集合：$N=\{S,A,B\}$
• 终结符集合：$\mathrm{\Sigma }=\{a,b\}$
• 产生式规则：
  1. $S\to aA$
  2. $A\to aA$
  3. $A\to bbB$
  4. $B\to bB$
  5. $B\to b$

该文法的推导过程：

1. 从 $S$ 开始：
   • 只能通过 $S\to aA$ 产生一个 $a$，然后变成 $A$。
2. $A$ 可能通过：
   • $A\to aA$ 继续生成 $a$，这意味着 $A$ 生成一个或多个 $a$。
   • $A\to bbB$ 进入 $b$ 的部分，且必须至少有两个 $b$。
3. $B$ 产生 一个或多个 $b$ 直到终结。

该文法生成的语言为：

$$L(G)=\{a^n{b}^m\mid n\ge 1,m\ge 3\}$$

即：

• $a^n$ 说明 $n$ 至少为 1（即至少一个 $a$）。
• $b^m$ 说明 $m$ 至少为 3（即至少三个 $b$）。
• 结构示例：
  • $abbb$
  • $aabbbb$
  • $aaabbbbb$

这个文法 不是正则语法，因为它包含了规则 $A\to bbB$（一个非终结符右侧带有多个终结符），不符合正则语法的限制。因此，它属于上下文无关文法（CFG）。

2.7 上下文有关文法 必考

3. CFG

3.1 CFG 产生的语言句子的派生树表示

• 派生树是一种树形结构，用于可视化一个句子的推导过程。

  • 根节点是起始符号 $S$。

  • 内部节点是非终结符，每个非终结符根据产生式继续展开。

  • 叶子节点是终结符，形成最终的字符串。

• 派生树的作用：

  • 直观地展示句子的生成过程。
  • 解析器（parser）可以利用它分析输入是否符合语法规则。

例子

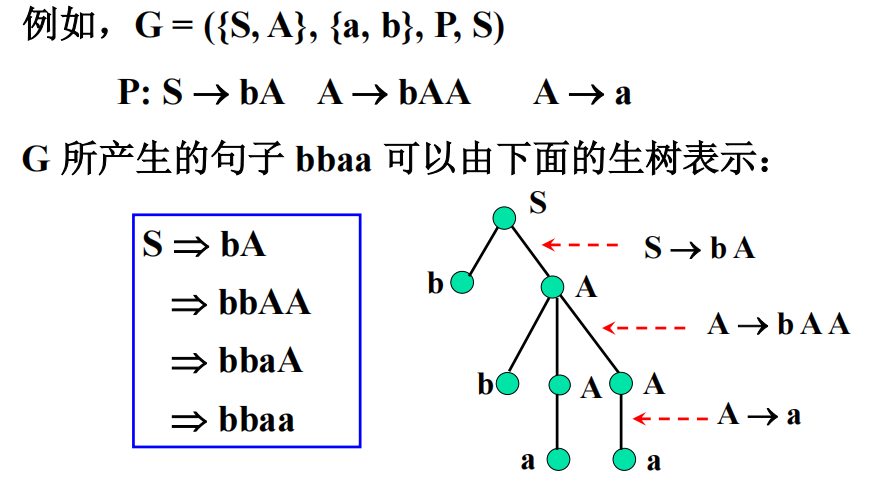
3.2 CFG的二义性

如果一个上下文无关文法（CFG）**能用**两种不同的方式生成同一个字符串，那么这个文法就是二义性文法（Ambiguous Grammar）。

简单理解： 同一个句子，可以有两棵不同的派生树（Parse Tree）或者两种不同的推导方式。

4. 自动机

自动机（Automaton）是一种数学模型，用于模拟计算过程，它接受或拒绝输入字符串，决定某个字符串是否属于特定语言。自动机在计算理论和编译原理中有广泛应用。

4.1 定义

自动机的核心组成部分：

• 状态集合（States）：表示系统的不同情况，通常用 $Q$ 表示。

• 输入字母表（Alphabet）：定义可接受的输入符号集合，通常用 $\Sigma$ 表示。

• 状态转移函数（Transition Function）：决定了在某个状态接收到输入后如何转移到下一个状态，通常用 $\delta$ 表示。

• 初始状态（Start State）：计算开始时的状态，通常用 $q_0$ 表示。

• 接受状态（Accept States）：如果输入结束时，自动机处于这些状态之一，则接受该输入，通常用 $F$ 表示。

想象你去坐地铁：

1. 你在**起点站（初始状态）**上车。
2. 你根据地铁线路图（规则），随着地铁运行到不同的站点（状态）。
3. 如果你到达了目标站（接受状态），你可以下车，表示这个路线是正确的（接受）。
4. 如果你中途走错了或者线路终点不对，那就说明这个路线是无效的（拒绝）。

4.2 语言与识别器的对应关系

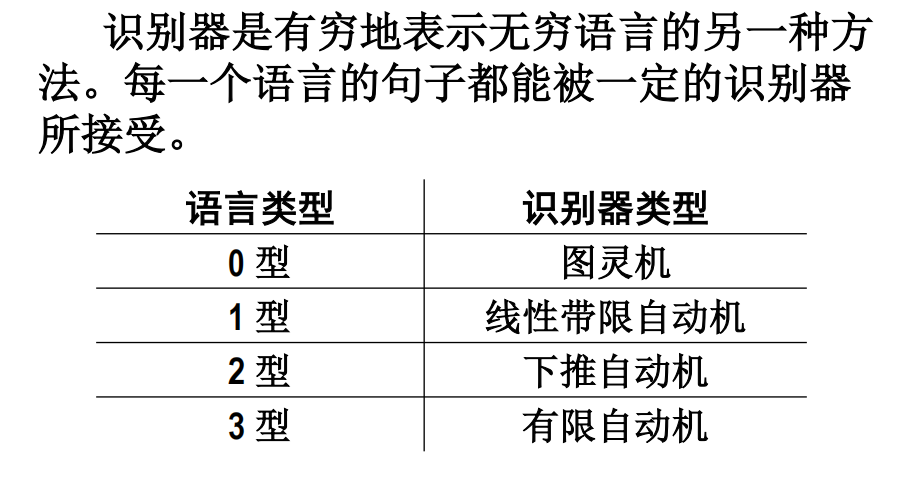
自动机类型	通俗解释
有限自动机（Finite Automaton, FA）	只能记住有限个状态，比如红绿灯，只有“红灯、黄灯、绿灯”三个状态，不能存储过去的信息。
下推自动机（Pushdown Automaton, PDA）	记忆能力更强，带有一个“备忘录”（栈），比如你在编程时匹配括号是否成对。
线性有界自动机（Linear Bounded Automaton, LBA）	可以处理更复杂的情况，比如自然语言语法，它能理解更长的规则。
图灵机（Turing Machine）	最强大的自动机，能模拟所有计算机程序，比如你的智能手机或电脑都可以被看作是一个图灵机。

4.3 有限自动机与正则文法

4.3.1 确定的有限自动机 DFA

DFA 由五个部分组成，数学表示为：

$$M=(\mathrm{\Sigma },Q,\delta ,q_0,F)$$

其中：

1. $\mathrm{\Sigma }$（输入符号集）：DFA 接受的所有输入符号的有限集合（例如 {0,1} 表示二进制输入）。
2. $Q$（状态集合）：自动机可能处于的所有有限状态的集合。
3. $q_0\in Q$（初始状态）：计算开始时的状态，只有一个。
4. $F\subseteq Q$（终止状态集合）：如果自动机最终停留在这些状态之一，则输入被接受。
5. $\delta :Q\times \mathrm{\Sigma }\to Q$（状态转移函数）：
   • 定义当前状态 $q$ 在接收输入 $a$ 后转移到哪个新状态 $q^{\prime }$。
   • 确定性：对于每个状态 $q$ 和每个输入符号 $a$，只能有一个唯一的转移（不会有多个选择）。

例子：

图示：

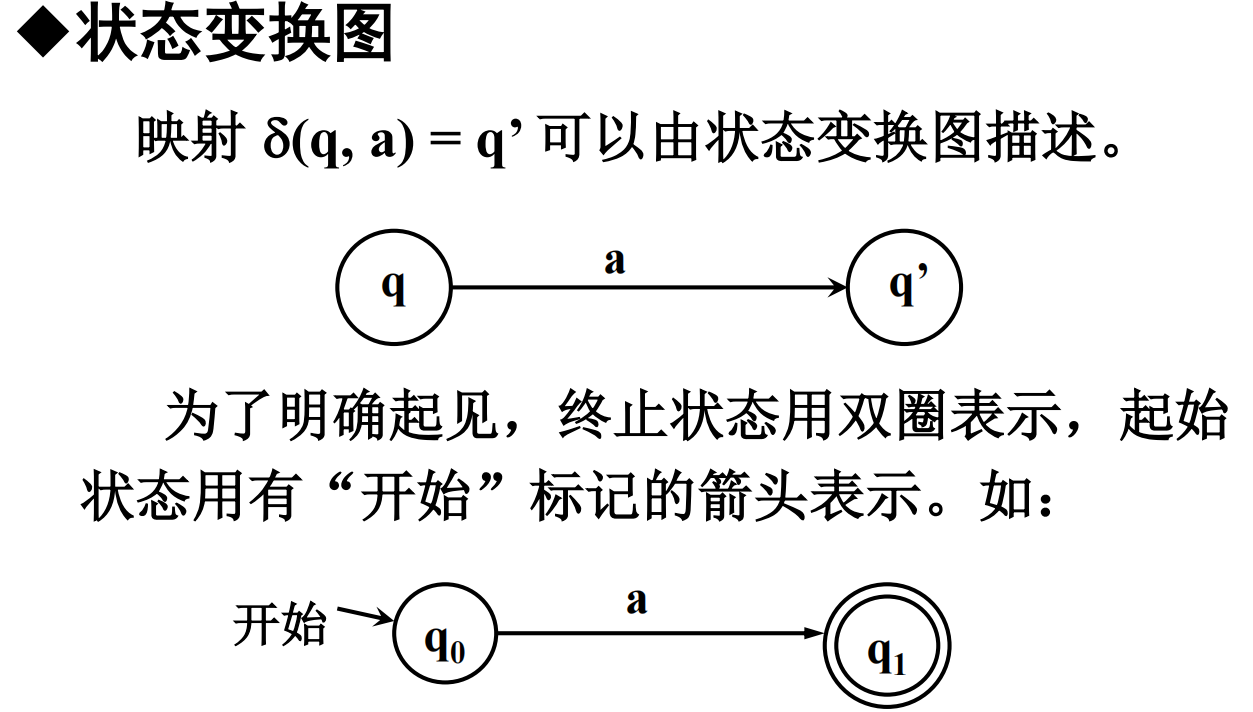
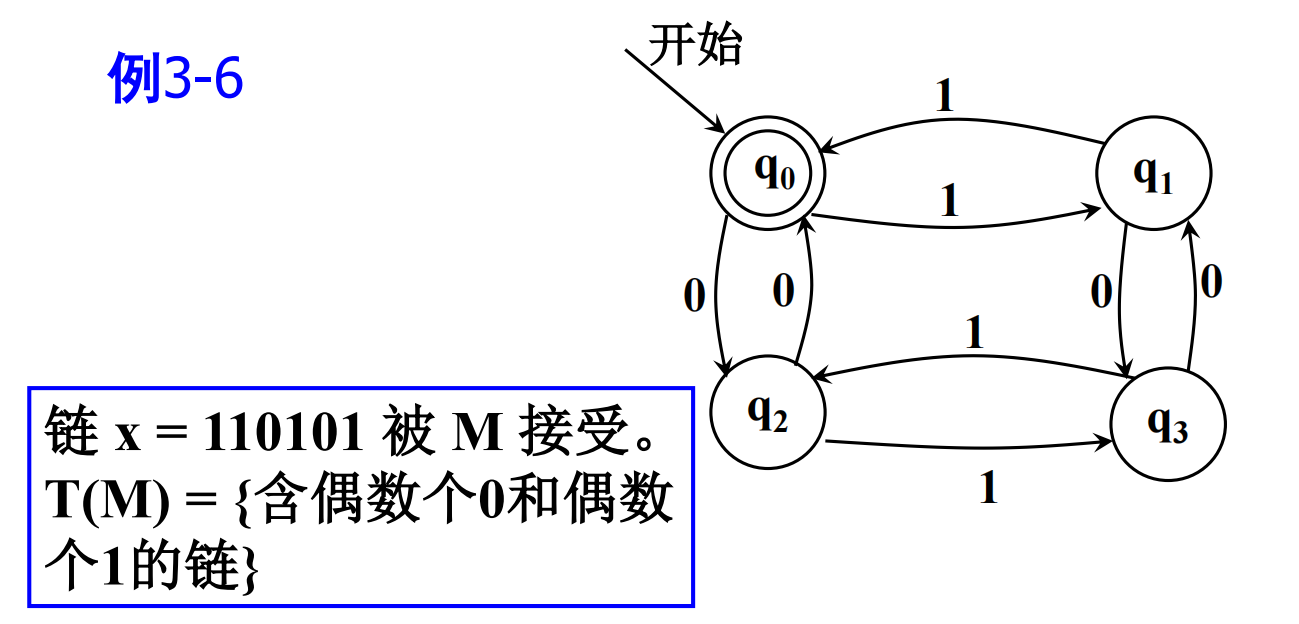
4.3.2 不确定的有限自动机 NFA

一个 NFA 由五个部分组成：

$$M=(\mathrm{\Sigma },Q,\delta ,q_0,F)$$

其中：

1. $\mathrm{\Sigma }$：输入符号的有限集合（字母表）。
2. $Q$：状态的有限集合。
3. $q_0\in Q$：初始状态（唯一）。
4. $F\subseteq Q$：终止状态集合，若计算完成时停在这些状态之一，则输入被接受。
5. $\delta :Q\times \mathrm{\Sigma }\to 2^Q$（状态转移函数）：
   • 从 当前状态 $q$ 和 输入符号 $a$ 出发，NFA 可能有多个可选的下一步状态。
   • 由于状态可能有多个选项，$\delta$ 的输出是状态集合（而不是单个状态）。

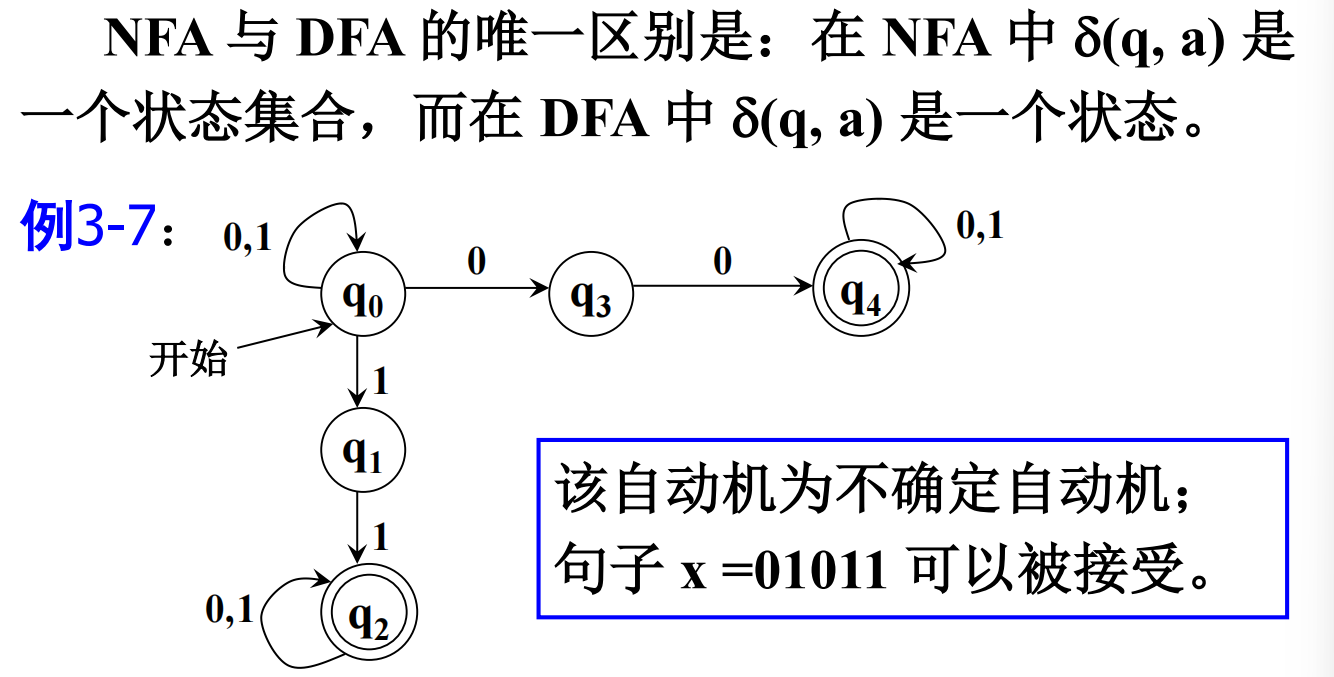
4.3.3 DFA & NFA

想象你在一个迷宫里寻找出口：

• DFA（确定性）：在每个十字路口，你只能选一个方向走（规则非常严格）。
• NFA（非确定性）：在每个十字路口，你可以选择多个路径同时尝试（就像有多个分身同时探索迷宫）。
• 只要有一个分身找到了出口，整个 NFA 就算成功接受了输入.

对比项	DFA（确定性有限自动机）	NFA（非确定性有限自动机）
状态转移	每个状态和输入符号只有一个可能的下一个状态	每个状态和输入符号可以有多个可能的下一个状态
计算方式	严格按照单一路径执行	可以“同时”沿多个路径执行（多线程感觉）
是否有 $ϵ$ 转移？	不允许 $ϵ$ 转移	允许 $ϵ$ 转移（可在无输入时跳转状态）
实现难度	相对简单，易于实现	结构更灵活，但实现复杂
等价性	可以直接转换为 NFA	NFA 可以转换成等价的 DFA（但可能状态数指数级增长）

4.3.4 正则文法和有限自动机

该定理说明：

• 每个正则文法都可以转换为一个有限自动机（FA）。
• 每个有限自动机（FA）都能对应一个正则文法。
• 正则文法的语言 $L(G)$ 等价于有限自动机识别的语言 $T(M)$，即： $T(M)=L(G)$

换句话说，正则文法与有限自动机是等价的，它们描述了相同的一类语言（正则语言）。

4.3.5 正则文法到自动机步骤

（1）定义自动机的基本元素

设定自动机的符号系统

• $\mathrm{\Sigma }$ 是输入字母表（终结符集合）。
• $Q$ 是状态集合，它由所有的非终结符 $V_N$ 加上一个额外的终止状态 $T$ 组成。
• $q_0=S$ 设定初始状态为 $S$。
• $T$ 是新增的终结状态，它用于表示字符串符合规则并被接受。

例子

给定正则文法：

1. $S\to aA$
2. $A\to bT$ （$T$ 代表终止）

那么：

• 状态集合：$Q=\{S,A,T\}$
• 输入符号：$\mathrm{\Sigma }=\{a,b\}$
• 初始状态：$S$
• 终止状态：$T$

---

（2）处理空串规则

• 如果文法中有规则 $S\to ϵ$（意味着空字符串也应该被接受），那么我们让 $S$ 本身就是终止状态，即： $F=\{S,T\}$
• 如果没有空串规则，则只有 $T$ 作为终止状态： $F=\{T\}$

例子

如果文法有：

• $S\to ϵ$（允许空字符串），那么 $S$ 本身就是终止状态，所以 $F=\{S,T\}$。
• 如果没有 $S\to ϵ$，那么 $F=\{T\}$。

---

（3）处理单独的终结符产生式

如果文法有形如：

$$B\to a$$

即 某个非终结符 $B$ 直接生成终结符 $a$，那么意味着：

• 从状态 $B$ 读取字符 $a$ 后，直接进入终止状态 $T$： $T=\delta (B,a)$

例子

文法：

1. $S\to aA$
2. $A\to b$ （意味着 $A$ 直接变成 $b$）

转换成自动机：

• $S\stackrel{a}{\to }A$
• $A\stackrel{b}{\to }T$ （$A$ 看到 $b$ 直接进入终止状态）

---

（4）处理带非终结符的产生式

如果文法有形如：

$$B\to aC$$

即 某个非终结符 $B$ 读取 $a$ 后变成 $C$，那么自动机状态变化为：

• 从状态 $B$ 读取 $a$ 后，进入状态 $C$： $C=\delta (B,a)$

例子

文法：

1. $S\to aA$
2. $A\to bB$
3. $B\to c$ （意味着 $B$ 直接变成 $c$）

转换成自动机：

• $S\stackrel{a}{\to }A$
• $A\stackrel{b}{\to }B$
• $B\stackrel{c}{\to }T$

这样，状态转换图可以表示为：

    S --(a)--> A --(b)--> B --(c)--> T

如果输入是 "abc"，那么这个字符串会被自动机接受。

---

（5）终止状态的规则

对于终止状态 $T$，它不再有任何转移：

$$\delta (T,a)=\mathrm{\varnothing }$$

即 终止状态 $T$ 不会有任何后续状态，输入任何字符都不会跳转。

例子

如果你在终止状态 $T$，不管输入什么字符，都会被拒绝（因为已经接受完成）。

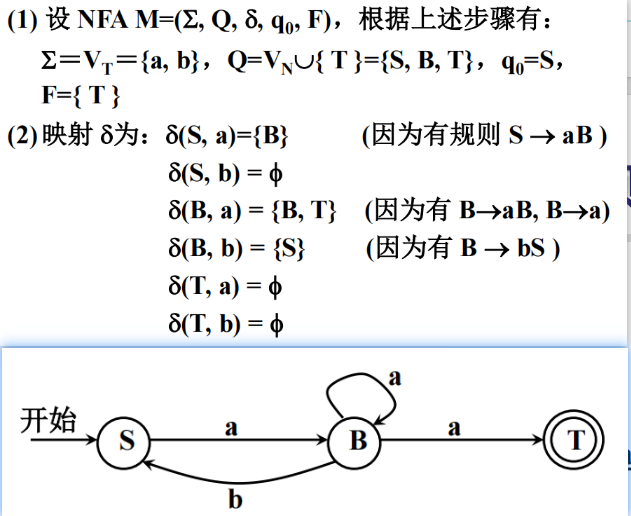
必考

image-20250317101722019

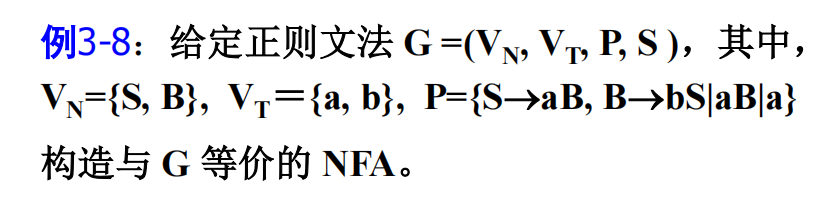
答

状态集合

$$Q=\{S,B,T\}$$

• $S$：初始状态
• $B$：中间状态
• $T$：终止状态（接受状态）

输入符号

$$\mathrm{\Sigma }=\{a,b\}$$

状态转移函数（NFA 规则）

当前状态	读入字符	转移状态
$S$	$a$	$B$
$B$	$b$	$S$
$B$	$a$	$B$
$B$	$a$	$T$

终止状态

$$F=\{T\}$$

4.3.6 状态变换图

4.4 CFG与下推自动机

4.4.1 PDA

基本概念

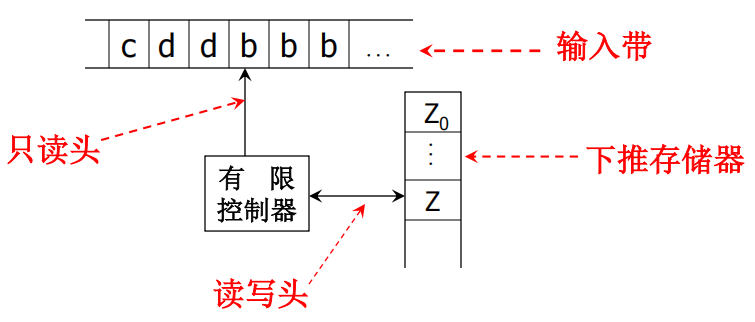
PDA 可以看作是一个带有栈（Stack）存储器的有限自动机，其特点包括：

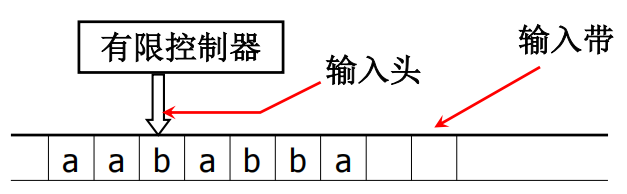
• 输入带（Input Tape）：像 DFA/NFA 一样，它从左到右读取输入字符。

• 有限控制器（Finite Control）：它决定状态如何变化。

• 下推存储器（Stack Storage）：一个额外的

  栈（stack），可以存取无限长的信息。

  • PDA 可以读取栈顶元素。
  • PDA 可以向栈顶写入新元素（Push）。
  • PDA **可以从栈顶弹出元素（Pop）**。

栈的作用：PDA 之所以比 DFA 更强大，是因为它能够记住历史信息，这对于处理嵌套结构（如括号匹配）至关重要。

数学定义

一个 PDA 由 7 元组表示：

$$M=(\mathrm{\Sigma },Q,\mathrm{\Gamma },\delta ,q_0,Z_0,F)$$

其中：

• $\mathrm{\Sigma }$：输入符号的有限集合（即输入字母表）。

• $Q$：有限个状态的集合。

• $\mathrm{\Gamma }$：栈符号的有限集合（即可以存入栈的符号）。

• $q_0$：初始状态。

• $Z_0$：栈的初始符号（默认栈底符号）。

• $F\subseteq Q$：终止状态集合（如果 PDA 进入终止状态，输入被接受）。

• $\delta$

  （状态转移函数）：描述状态如何变化：

  $$\delta :Q\times (\mathrm{\Sigma }\cup \{ϵ\})\times \mathrm{\Gamma }\to P(Q\times {\mathrm{\Gamma }}^{\ast })$$

  在某个状态 $q$，读取输入带上的符号 $a$（或 $ϵ$），同时查看栈顶符号 $X$，然后决定：

  • 进入哪个新状态 $q^{\prime }$。
  • 是否弹出（Pop） 栈顶符号。
  • 是否压入（Push） 一个或多个符号到栈中。