判别模型

距离判别

1. 两组判别

1.1 一般的两组距离判别

• 每一组有自己的均值向量${\mu }_1,{\mu }_2$ 和协方差矩阵 ${\mathrm{\Sigma }}_1,{\mathrm{\Sigma }}_2$。

• 判别准则是比较两组的 马氏距离（Mahalanobis Distance）： $d_1(x)=(x-{\mu }_1{)}^T{\mathrm{\Sigma }}_1^{-1}(x-{\mu }_1),d_2(x)=(x-{\mu }_2{)}^T{\mathrm{\Sigma }}_2^{-1}(x-{\mu }_2)$

  判别样本 $x$ 属于哪一类，取决于：

  $\text{若 }{d}_1(x)<d_2(x),\text{ 则 }x\text{ 属于组 1；否则属于组 2。}$

1.2 协方差矩阵相等的情况

• 假设 ${\mathrm{\Sigma }}_1={\mathrm{\Sigma }}_2=\mathrm{\Sigma }$，此时判别准则可以简化为：

  $d(x)=(x-{\mu }_1{)}^T{\mathrm{\Sigma }}^{-1}(x-{\mu }_1)-(x-{\mu }_2{)}^T{\mathrm{\Sigma }}^{-1}(x-{\mu }_2)$

• 展开计算后，最终得到一个 线性判别函数： $g(x)=w^{T}x+w_0$其中，权重向量 w 和偏置 $w_0$ 定义为：

  $w={\mathrm{\Sigma }}^{-1}({\mu }_1-{\mu }_2),w_0=-\frac{1}{2}({\mu }_1^T{\mathrm{\Sigma }}^{-1}{\mu }_1-{\mu }_2^T{\mathrm{\Sigma }}^{-1}{\mu }_2)$

  判别规则为：$ \text{若 } g(x) > 0, \text{ 则 } x \text{ 属于组 1；否则属于组 2。}$

区别：

• 当协方差矩阵不同时，需要分别考虑不同方向的缩放，判别边界通常为 二次曲线。
• 当协方差矩阵相等时，判别边界为 线性超平面，即一个直线（二维）或超平面（高维）。

误判概率的来源

• 判别错误的概率与两组数据的分布、均值 ${\mu }_1,{\mu }_2$、以及协方差矩阵 $\mathrm{\Sigma }$ 有直接关系。
• 假设两组数据均服从多元正态分布： $x\sim \mathcal{N}({\mu }_1,\mathrm{\Sigma }),x\sim \mathcal{N}({\mu }_2,\mathrm{\Sigma })$ 判别的误判概率主要受两组分布的 重叠程度 影响。

协方差矩阵相等时的误判概率

• 当 ${\mathrm{\Sigma }}_1={\mathrm{\Sigma }}_2$，判别的决策边界为：

  $g(x)=w^{T}x+w_0$

  • 边界为线性超平面。
  • 若两组数据的分布有较大重叠，则误判概率增加。
  • 判别的误判概率由正态分布的 累积分布函数 给出。

误判概率比较

• 若两组数据的协方差矩阵差异较大，使用相等协方差矩阵可能导致边界不准确，从而误判概率升高。
• 如果两组数据的协方差矩阵本来就接近相等，则二者误判概率差异不大。

1.3 误判概率的非参数估计

1. 回代法

• 原理：使用训练样本自身对判别函数进行评估，通过统计训练样本被误判为其他类别的比例，估计误判概率。
• 缺点：可能存在乐观估计，因为训练样本的判别信息被重复使用，导致估计偏低。

2. 划分样本法

• 原理：将样本分为训练集和验证集，用训练集构造判别函数，用验证集估计误判概率。验证集的误判比例通常无偏。
• 缺点：需要较大样本量且训练集信息不足可能导致判别函数质量下降。

3. 交叉验证法（刀切法）

• 原理：对每个样本，移除其自身，使用剩余样本构造判别函数，再用该函数对被移除样本进行判别。重复操作并综合结果计算误判概率。
• 优点：有效避免样本信息重复使用和损失。

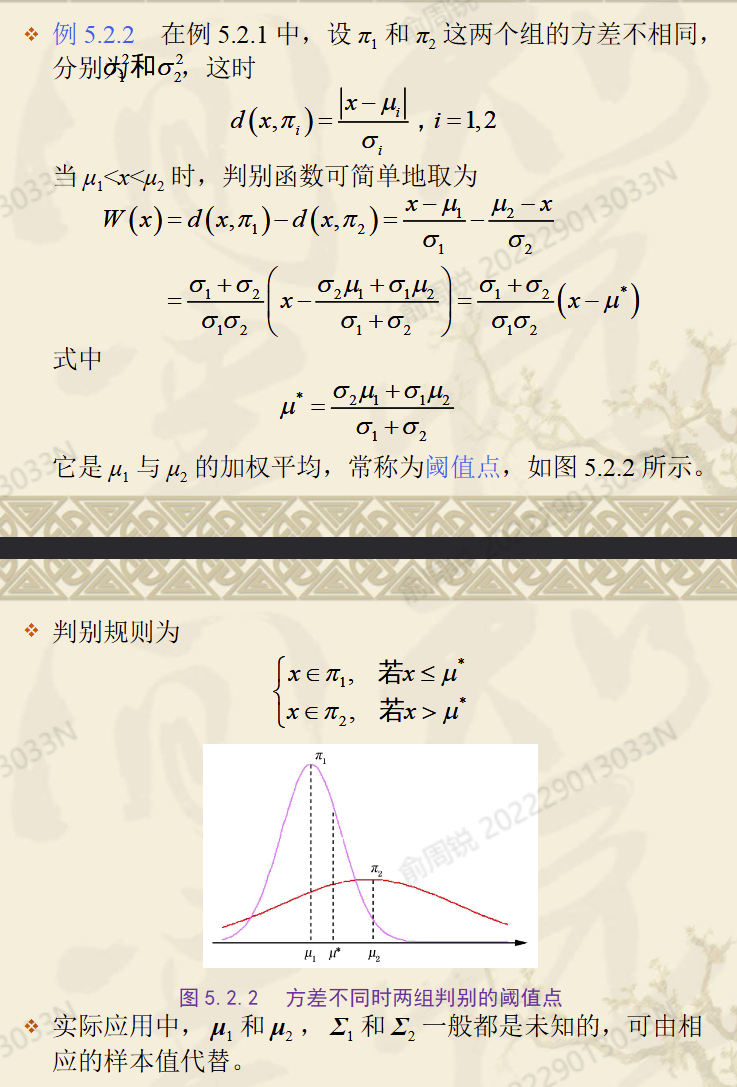
1.4 协方差不相等的情况

2. 多组判别

2.1 多组距离判别的核心原理：

• 当有 k 个组（如 ${\pi }_1,{\pi }_2,...,{\pi }_k$）时，每一组数据都可以用它们的均值向量 ${\mu }_i$ 和协方差矩阵 ${\mathrm{\Sigma }}_i$ 来描述。
• 对于一个样本点 x，计算它到每一组的马氏距离 $d^2(x,{\pi }_i)$，公式如下： $d^2(x,{\pi }_i)=(x-{\mu }_i{)}^{\prime }{\mathrm{\Sigma }}_i^{-1}(x-{\mu }_i),i=1,2,...,k$
• 判别规则：将 x 判别到马氏距离最小的那一组： $x\in {\pi }_i⟺d^2(x,{\pi }_i)=\underset{1\le i\le k}{min}{d}^2(x,{\pi }_i)$

2.2 协方差一样

• 如果所有组的协方差矩阵相等 ${\mathrm{\Sigma }}_1={\mathrm{\Sigma }}_2=...={\mathrm{\Sigma }}_k=\mathrm{\Sigma }$，那么公式可以被简化。
• 判别规则转换为计算线性判别函数 $I_i^{\prime }x+c_i$，其中： $I_i={\mathrm{\Sigma }}^{-1}{\mu }_i,c_i=-\frac{1}{2}{\mu }_i^{\prime }{\mathrm{\Sigma }}^{-1}{\mu }_i$
• 判别规则变为：比较每组的 $I_i^{\prime }x+c_i$ 值，选择最大的那一组。

2.3 协方差不全相等

image-20241227202440564

贝叶斯判别

最大后验概率法的原理

• 定义：对于有 k 个分组 ${\pi }_1,{\pi }_2,\dots ,{\pi }_k$，每组有对应的概率密度函数 $f_i(x)$ 和先验概率 $p_i$。
• 后验概率计算公式：$P({\pi }_i|x)=\frac{p_i{f}_i(x)}{\sum _{j=1}^k{p}_j{f}_j(x)}$ 表示样本 x 属于组 ${\pi }_i$ 的概率。
• 判别规则：将 x 判别为后验概率最大的组： $x\in {\pi }_l$, $\text{若 }P({\pi }_l|x)=\underset{1\le i\le k}{max}P({\pi }_i|x)x\in \pi l,$