多元统计与数字分析 1

1. 定义

1.1 $p\times q$ 矩阵

矩阵

• $p\times q$ 矩阵：A 的形状由 p 行和 q 列组成。
• 矩阵 A 的一般表示法：$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1q}\\ a_{21}& a_{22}& \cdots & a_{2q}\\ ⋮& ⋮& \ddots & ⋮\\ a_{p1}& a_{p2}& \cdots & a_{pq}\end{array}\right)$

向量

• 列向量 a：是一个 $p-$ 维的列向量，表示为： $a=\left(\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_p\end{array}\right)$
• 行向量 $b\prime$：是一个 $q-$ 维的行向量，表示为： $b^{\prime }=(b_1,b_2,\cdots ,b_q)$

向量的长度

• 向量 a 的长度定义为： $\parallel a\parallel =\sqrt{a^{\prime }a}=\sqrt{a_1^2+a_2^2+\cdots +a_p^2}$如果向量是单位向量，则满足： $\parallel a\parallel =1$

1.2 其他概念

• 0 矩阵： $0=0_{pq}=(0):p\times q$

• $p$ 阶方阵

1.3 不同形态的矩阵

从图片内容来看，包含以下矩阵的基本概念和性质：

---

1. 矩阵分类：

• 上三角矩阵$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1p}\\ 0& a_{22}& \cdots & a_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & a_{pp}\end{array}\right)$ 特点：主对角线以下的元素全为零。

• 下三角矩阵$A=\left(\begin{array}{cccc}{a}_{11}& 0& \cdots & 0\\ a_{21}& a_{22}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ a_{p1}& a_{p2}& \cdots & a_{pp}\end{array}\right)$ 特点：主对角线上方的元素全为零。

• 对角矩阵$A=\left(\begin{array}{cccc}{a}_{11}& 0& \cdots & 0\\ 0& a_{22}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & a_{pp}\end{array}\right)$ 可表示为：

  $\text{diag}(a_{11},a_{22},\dots ,a_{pp})$

• 单位矩阵$I_p=\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right)$ 特点：主对角线全为 1，其他位置为 0。

---

2. 矩阵的转置：

• 矩阵 A 的转置定义为 $A^{\prime }=A^T$： 转置操作将矩阵的行变为列，列变为行： $A^T=\left(\begin{array}{cccc}{a}_{11}& a_{21}& \cdots & a_{p1}\\ a_{12}& a_{22}& \cdots & a_{p2}\\ ⋮& ⋮& \ddots & ⋮\\ a_{1q}& a_{2q}& \cdots & a_{pq}\end{array}\right)$

---

3. 对称矩阵：

• 矩阵 A 是对称矩阵当且仅当 $A=A^T$。 这意味着矩阵中满足 $a_{ij}=a_{ji}$。 举例：$\left(\begin{array}{cc}1& 3\\ 3& 4\end{array}\right),\left(\begin{array}{ccc}9& 0& 0\\ 0& 7& 0\\ 0& 0& 1\end{array}\right),\left(\begin{array}{ccc}2& 3& 5\\ 3& 0& 1\\ 5& 1& 1\end{array}\right)$

---

2. 矩阵的运算

2.1 基本运算

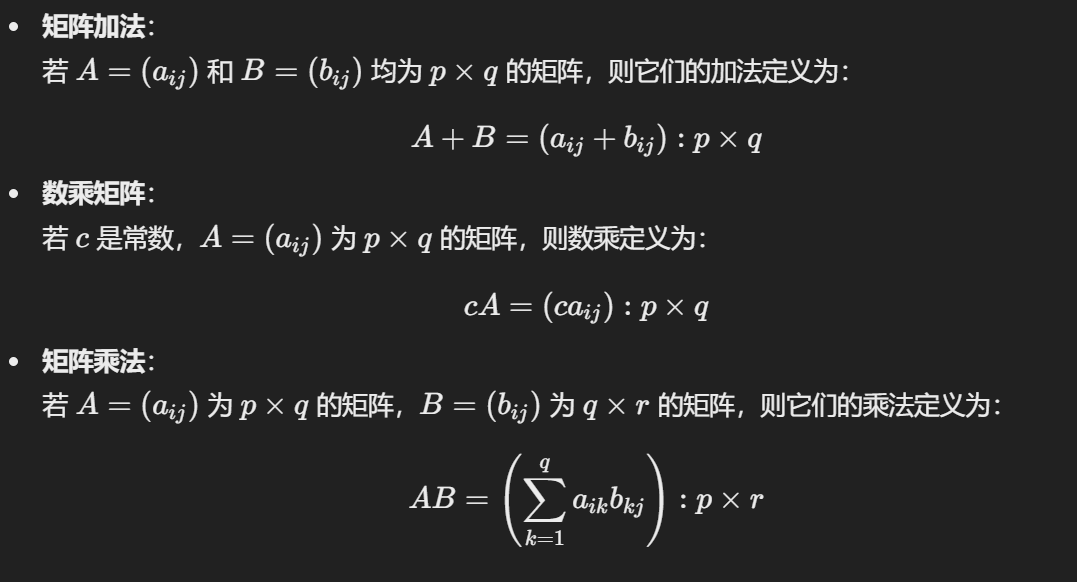
2.2 运算规律

转置的性质：

• $(A+B{)}^{\prime }=A^{\prime }+B^{\prime }$
• $(AB{)}^{\prime }=B^{\prime }{A}^{\prime }$

分配律：

• $A(B_1+B_2)=A{B}_1+A{B}_2$

加法的扩展性：

• $A\left(\sum _{i=1}^k{B}_i\right)=\sum _{i=1}^{k}A{B}_i$

数乘分配律：

• $c(A+B)=cA+cB$

2.3 正交

投影矩阵和幂等矩阵：

• 如果矩阵 A 满足 $A^2=A$，称 A 为幂等矩阵。
• 对称的幂等矩阵被称为投影矩阵。

正交矩阵的几何意义：

• 在二维情况下 ($p=2$)，正交矩阵对应的是坐标轴的旋转变换，例如：

  

  $y=Ax=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$

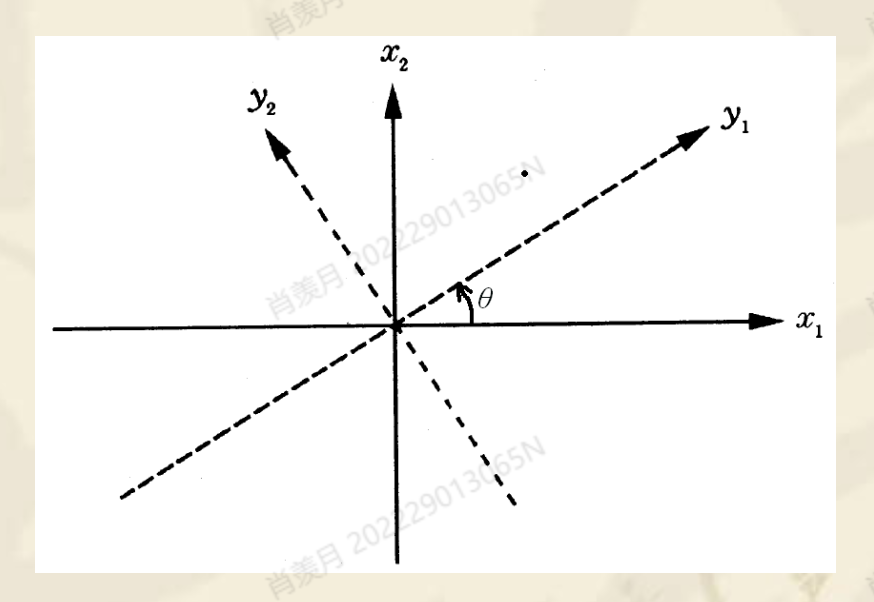
  这表示一个关于原点的旋转。

• 在三维情况下 ($p=3$)，正交矩阵也表示旋转变换。若 $|A|=1$，对应刚性旋转；若 $|A|=-1$，包含一个镜像反射的轴。

正交矩阵保持长度不变：

• 在正交变换下，点到原点的距离保持不变。这是由公式 $y^{\prime }y=(Ax{)}^{\prime }(Ax)=x^{\prime }{A}^{\prime }Ax=x^{\prime }x$ 推导出的。

2.3 矩阵的分块

3. 行列式

3.1 基本性质

3.2 代数余子式

例子

4. 矩阵的逆

4.1 基本定义

1. 矩阵的逆定义：

• 若矩阵 A 为一个 $n\times n$ 的方阵（必须是方阵），且存在矩阵 C 满足：$AC=CA=I$ 则称 C 为 A 的逆矩阵，记为 $A^{-1}$。

2. 非退化与退化矩阵：

• 非退化（非奇异）矩阵：行列式 $|A|\ne 0$，此时矩阵 A 有唯一的逆矩阵。
• 退化（奇异）矩阵：行列式 $|A|=0$，此时矩阵 A 不可逆。

3. $2\times 2$ 方阵的逆矩阵计算公式：

设：

$A=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]$

则：

$A^{-1}=\frac{1}{|A|}\left[\begin{array}{cc}{a}_{22}& -a_{12}\\ -a_{21}& a_{11}\end{array}\right]$

• $A|=a_{11}{a}_{22}-a_{12}{a}_{21}$ 是 A 的行列式。
• 条件：$|A|\ne 0$。

4.2 基本性质

5. 矩阵的秩

6. 特征值，特征向量和矩阵的迹

6.1 特征值，特征向量

6.2 基本性质 1, 2

例题

6.3 基本特征 3,4,5

6.4 矩阵的迹

公式表示

设矩阵 A 为一个 $n\times n$ 的方阵：

$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]$

则矩阵的迹（记作 $\text{tr}(A)$）定义为：

$\text{tr}(A)=\sum _{i=1}^n{a}_{ii}=a_{11}+a_{22}+\cdots +a_{nn}$

即矩阵主对角线上的所有元素的总和。

基本性质

正定