RNN模型训练

XiaoXianYue原创2025年4月14日大约 3 分钟

初始参数

import os
import math
import random
import urllib.request
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# =========================
# 自动下载数据
# =========================
file_path = "timemachine.txt"
url = "http://d2l-data.s3-accelerate.amazonaws.com/timemachine.txt"
if not os.path.exists(file_path):
    print("Downloading dataset...")
    urllib.request.urlretrieve(url, file_path)

# =========================
# 数据预处理
# =========================
with open(file_path, 'r', encoding='utf-8') as f:
    text = f.read().lower()
text = ''.join([line.strip() for line in text.split('\n') if line.strip()])

# 构建词表
vocab = sorted(list(set(text)))
vocab_size = len(vocab)
char2idx = {ch: i for i, ch in enumerate(vocab)}
idx2char = {i: ch for i, ch in enumerate(vocab)}
corpus = [char2idx[ch] for ch in text]


# =========================
# 获取 mini-batch 数据
# =========================
def get_batch(corpus, batch_size, num_steps):
    start = random.randint(0, len(corpus) - batch_size * num_steps - 1)
    inputs, targets = [], []
    for i in range(batch_size):
        idx = start + i * num_steps
        inputs.append(corpus[idx:idx + num_steps])
        targets.append(corpus[idx + 1:idx + num_steps + 1])
    return torch.tensor(inputs), torch.tensor(targets)


# =========================
# RNN 模型定义
# =========================
class RNNModel(nn.Module):
    def __init__(self, vocab_size, hidden_size):
        super().__init__()
        self.embedding = nn.Embedding(vocab_size, vocab_size)  # one-hot
        self.rnn = nn.RNN(vocab_size, hidden_size, batch_first=True)
        self.fc = nn.Linear(hidden_size, vocab_size)

    def forward(self, x, state):
        x = self.embedding(x)
        out, state = self.rnn(x, state)
        out = self.fc(out)
        return out, state

    def init_state(self, batch_size):
        return torch.zeros(1, batch_size, hidden_size)


# =========================
# 模型训练函数
# =========================
def train(model, corpus, num_epochs, batch_size, num_steps, lr):
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)
    loss_fn = nn.CrossEntropyLoss()
    perplexities = []

    for epoch in range(1, num_epochs + 1):
        state = model.init_state(batch_size)
        X, Y = get_batch(corpus, batch_size, num_steps)
        Y = Y.reshape(-1)
        logits, state = model(X, state)
        logits = logits.reshape(-1, vocab_size)
        loss = loss_fn(logits, Y)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        ppl = math.exp(loss.item())
        perplexities.append(ppl)
        print(f"Epoch {epoch}, Loss {loss.item():.4f}, Perplexity {ppl:.2f}")

    return perplexities


# =========================
# 参数设置 & 启动训练
# =========================
hidden_size = 128
batch_size = 32
num_steps = 35
lr = 1e-2
num_epochs = 20

model = RNNModel(vocab_size, hidden_size)
perplexity_list = train(model, corpus, num_epochs, batch_size, num_steps, lr)

# =========================
# 绘制 Perplexity 折线图
# =========================
plt.figure(figsize=(8, 5))
plt.plot(perplexity_list, marker='o')
plt.title("Perplexity over Epochs")
plt.xlabel("Epoch")
plt.ylabel("Perplexity")
plt.grid(True)
plt.tight_layout()
plt.savefig("perplexity_plot.png")
plt.show()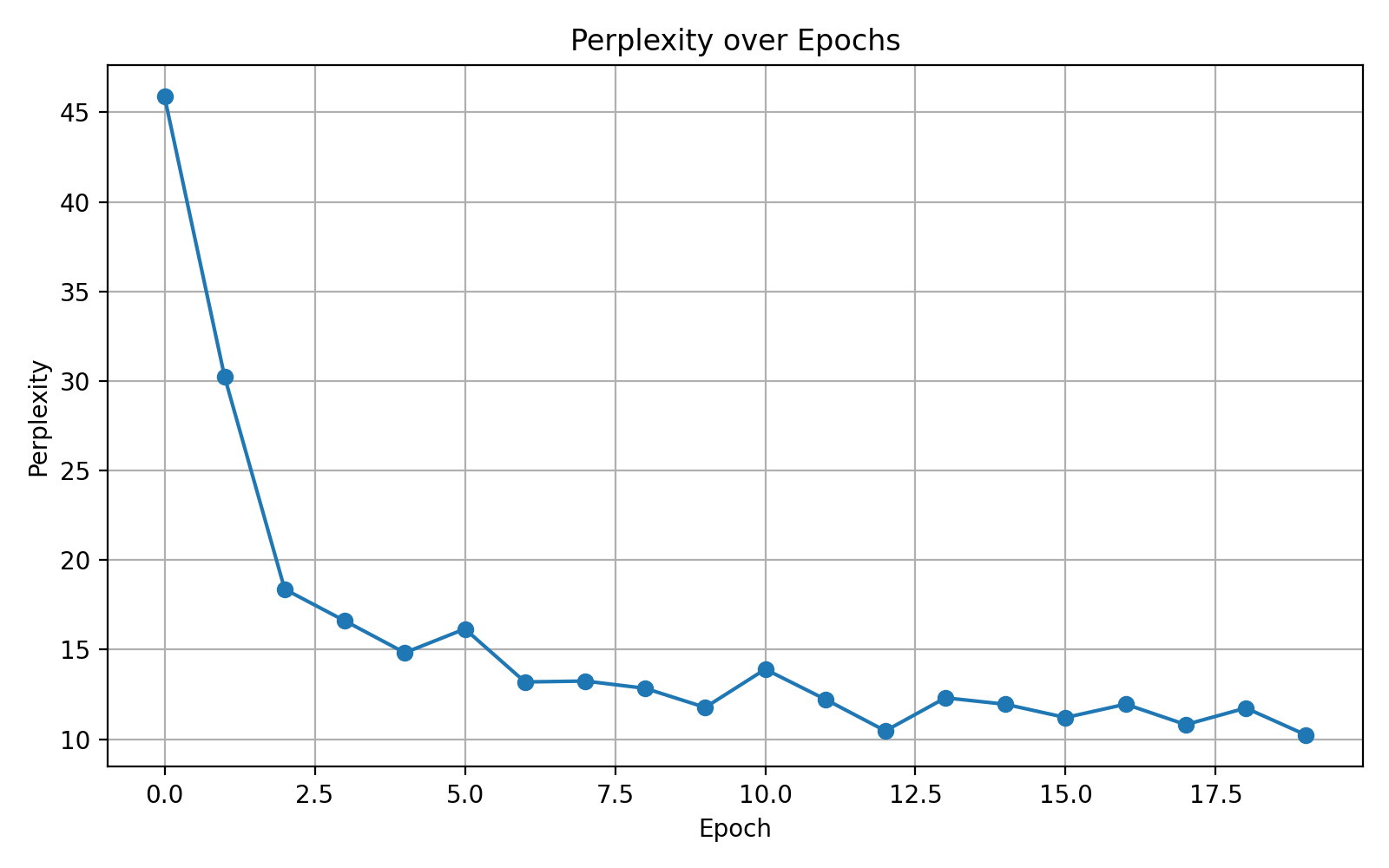

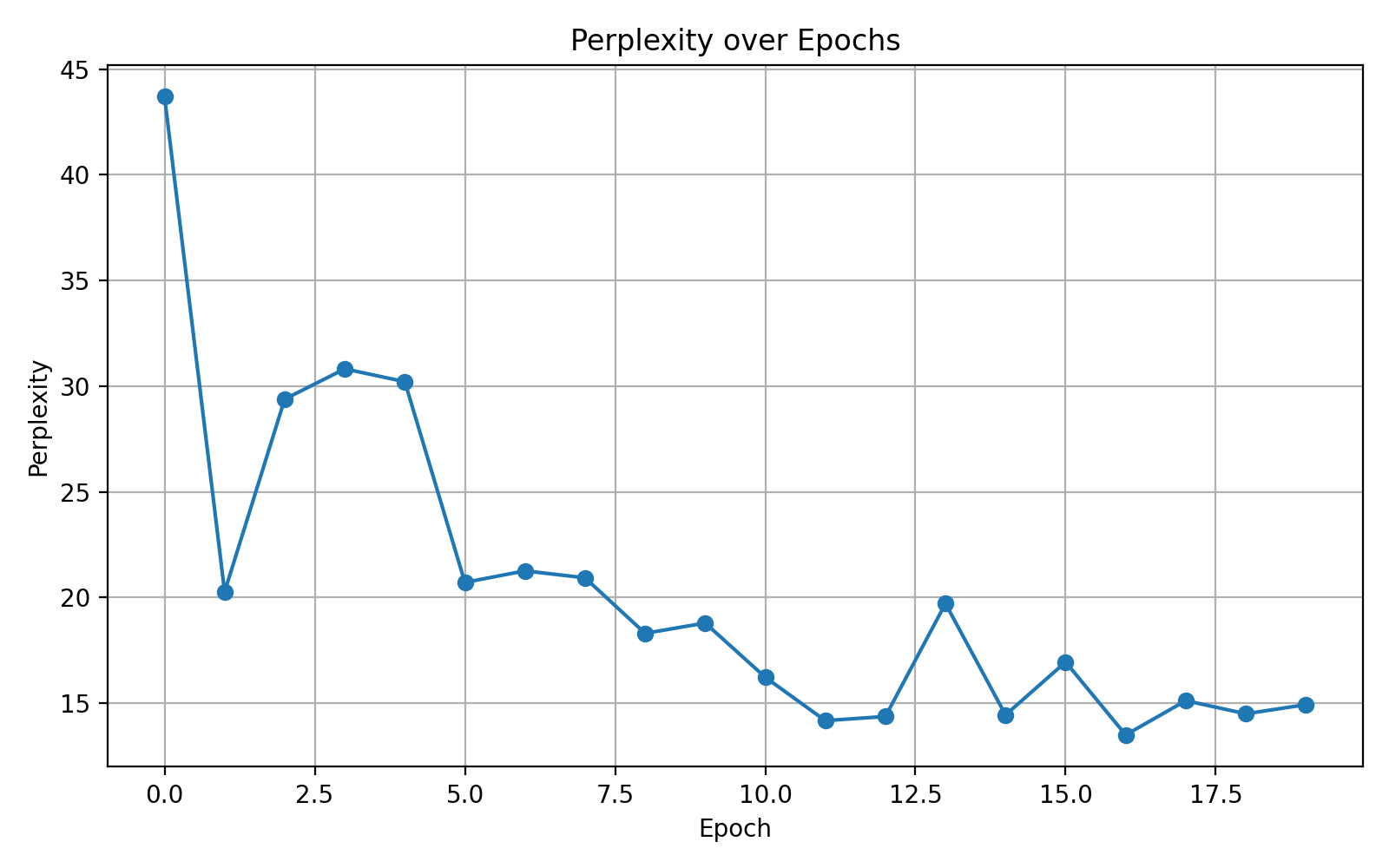
改变隐藏层维度

提高至 200：

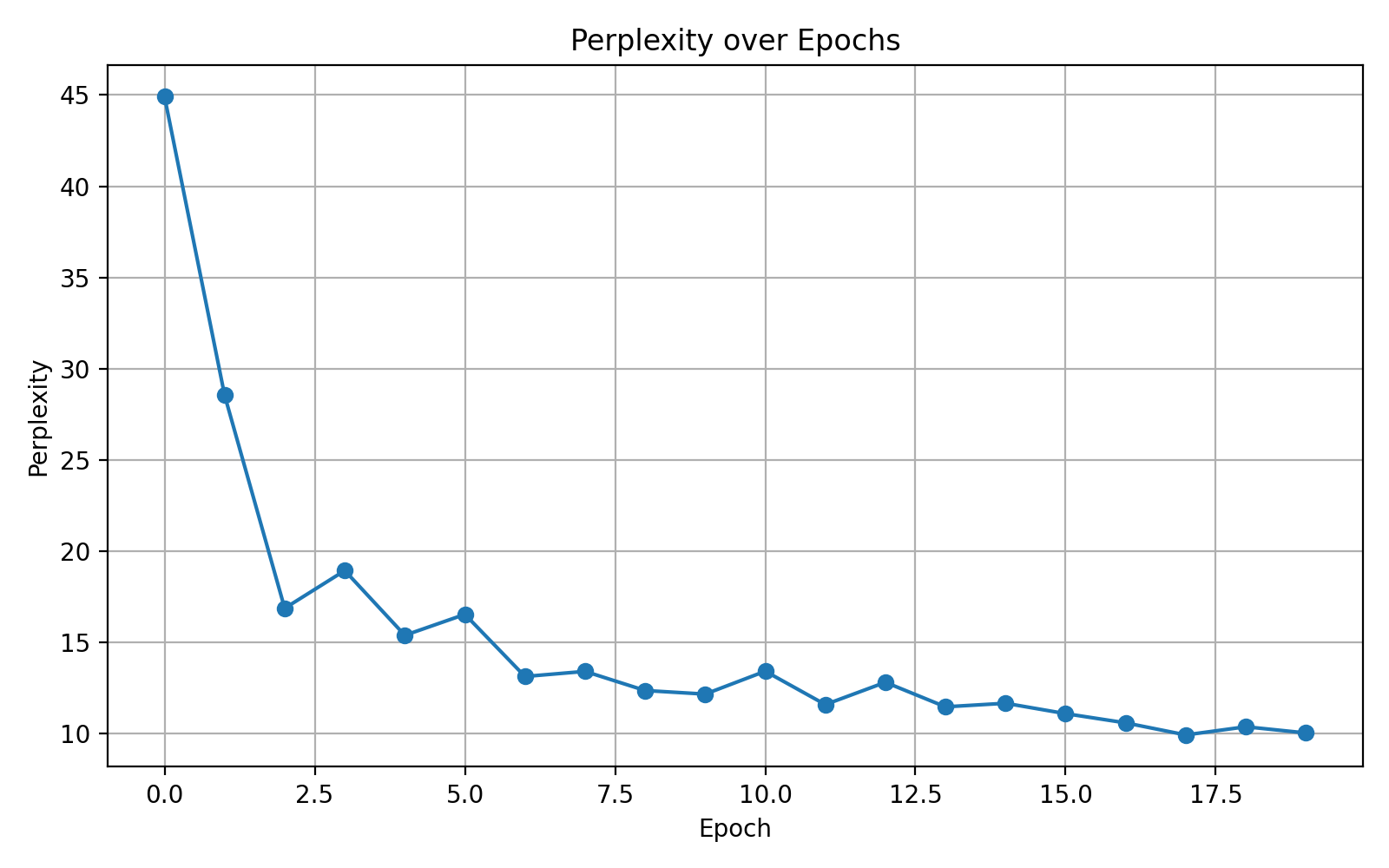
提高至 300：

维度	影响
小（128）	记忆力中等，学习稳定，但不够强
中（200）	记忆力加强，捕捉依赖能力提升，表现更好 ✅
大（300）	参数数目更多，训练难度加大，可能不容易收敛或震荡

我们选择最优参数，进一步调其他参数看看能不能越来越好。

调整批量大小:

32 调整为 16：

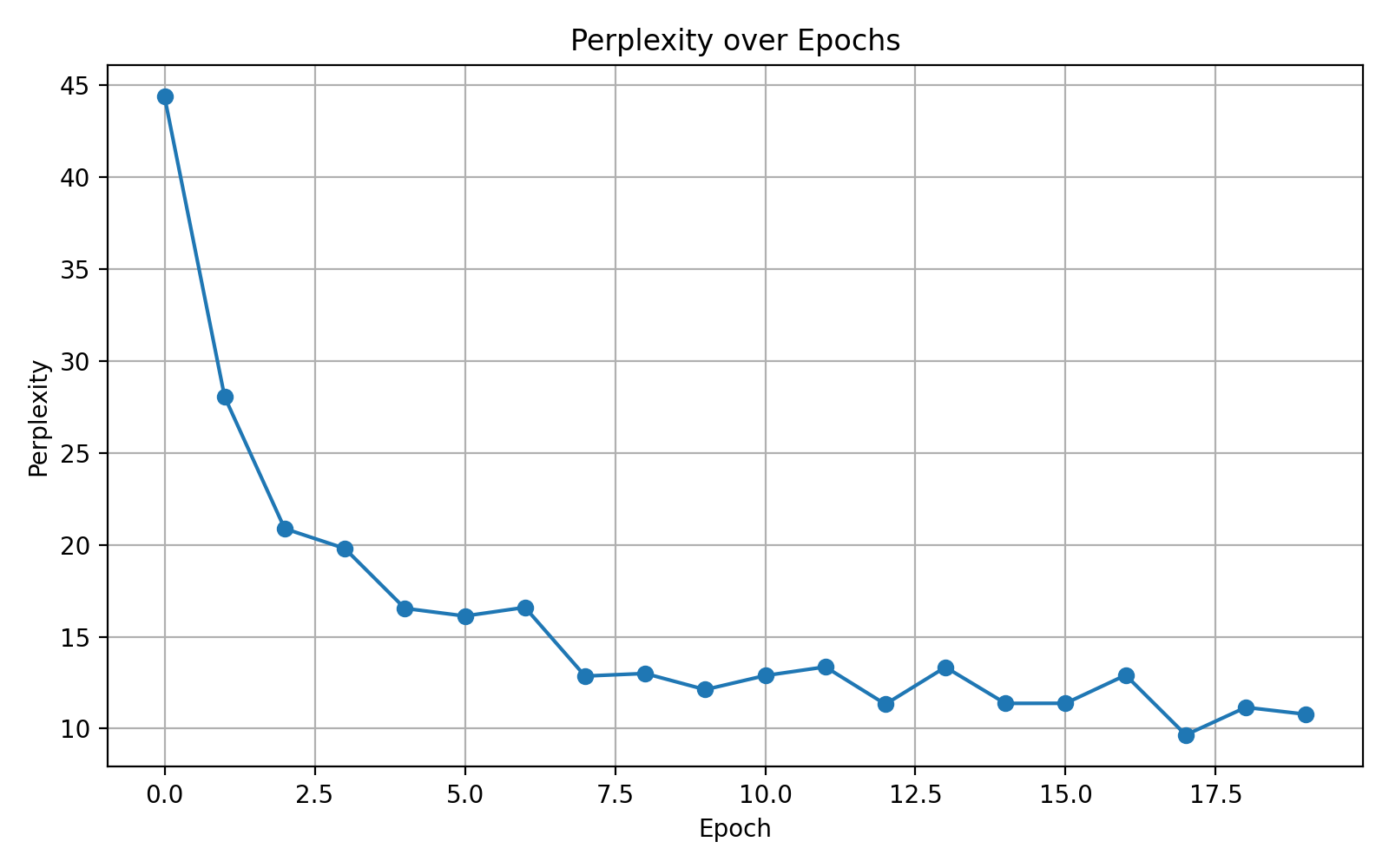
32 调整为 64：

Batch Size	收敛速度	波动性	最终 perplexity	特点
16	很快	明显波动	10 左右	梯度噪声大，更随机
32	中等	偏稳定	最佳平衡点 ✅	实用性强
64	稳定但慢	极平稳	与32相近	占用内存高，适合大模型