DL前三次课

1. pre concept

1. 1 线性回归和 Softmax 回归

线性回归 ——> 离散分类：

image-20250529111649192

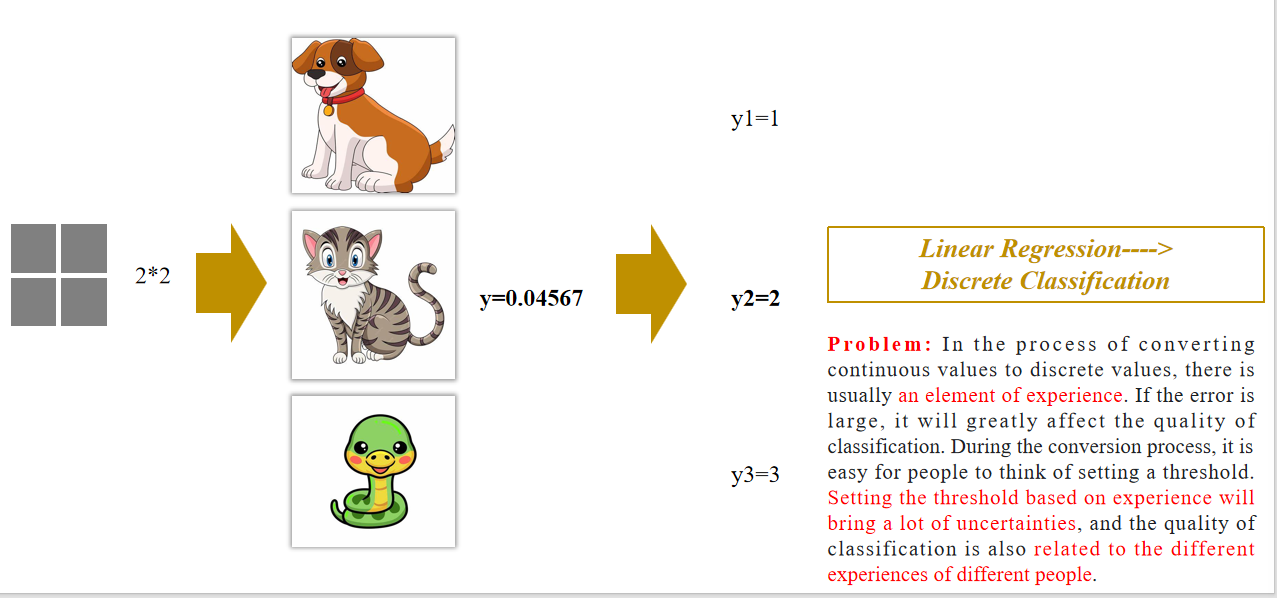
在将连续值转换为离散值的过程中，通常依赖于“经验因素”。如果误差较大，会严重影响分类质量。转换过程中人们往往会设置一个阈值。根据经验设定阈值会带来很多不确定性，而且分类质量因人而异，受到不同经验的影响。

• 阈值：threshold

softmax回归 ——> 离散分类

image-20250529111947035

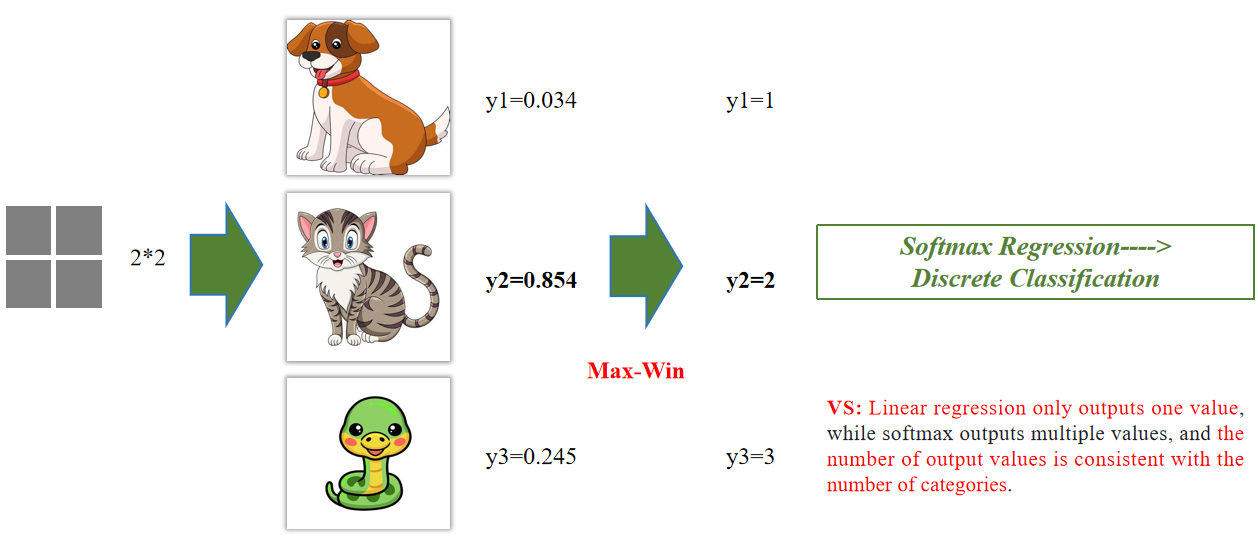
线性回归只输出一个值，而Softmax可以输出多个值，输出值的个数与类别数一致

解释：Softmax输出的是各个类别的概率分布，所以模型可以自动选出最有可能的类别，而不需要人为设置阈值。

1.2 Softmax 回归长什么样？

image-20250529112628441

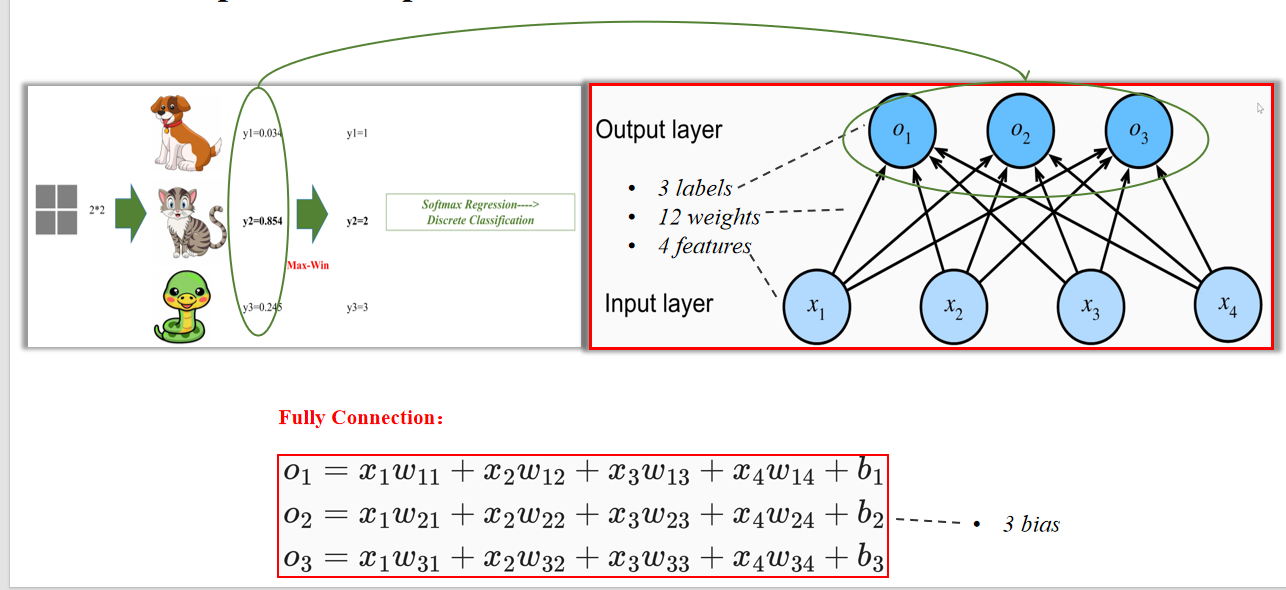
Input layer（输入层）

• 4个 features（如图中x₁~x₄）

Output layer（输出层）

• 3个 labels（对应狗、猫、蛇）
• 12个 weights（4特征 × 3输出）
• 外加3个偏置（bias）

1.3 Softmax回归模型如何输出分类结果

image-20250529113132954

Max-win 方法：

• “10”这个值没有实际意义，不具可解释性。

• 类别是离散的（1、2、3），输出是连续的，不能直接比较它们之间的“距离”。

Softmax算子：

• 使用 Softmax 后，输出是一个概率分布（总和为 1），范围在 [0, 1] 之间。

1.4 Softmax 数学过程

image-20250529113556483

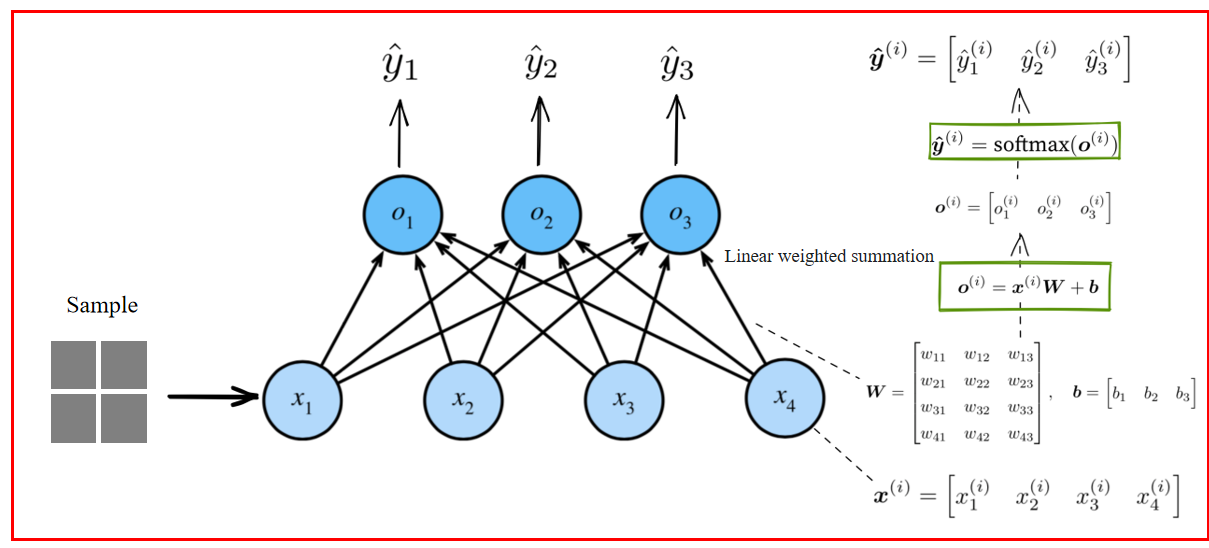
输入的维数增加：

image-20250529114048826

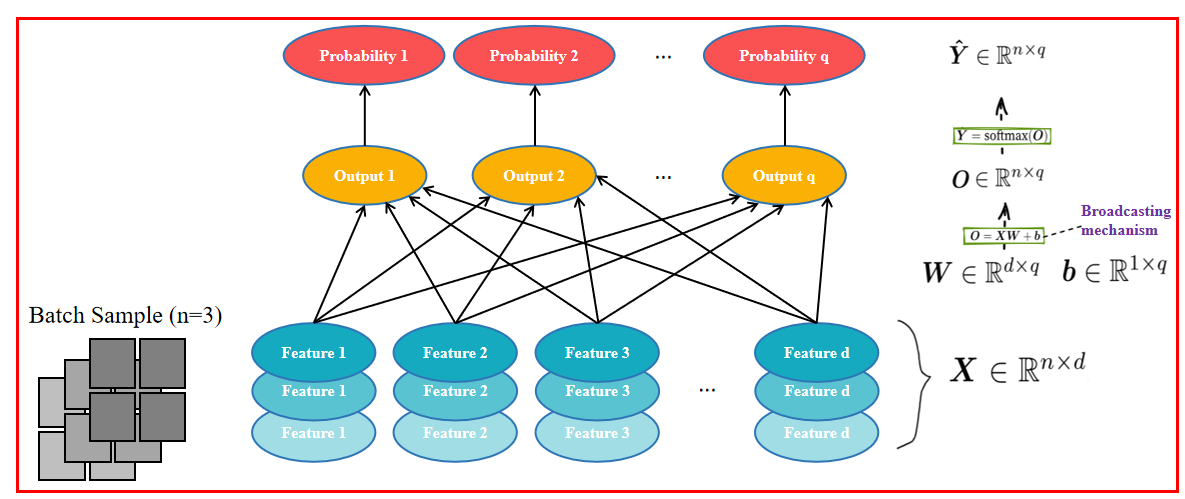
1.5 数学定义

1. 张量

image-20250529114459286

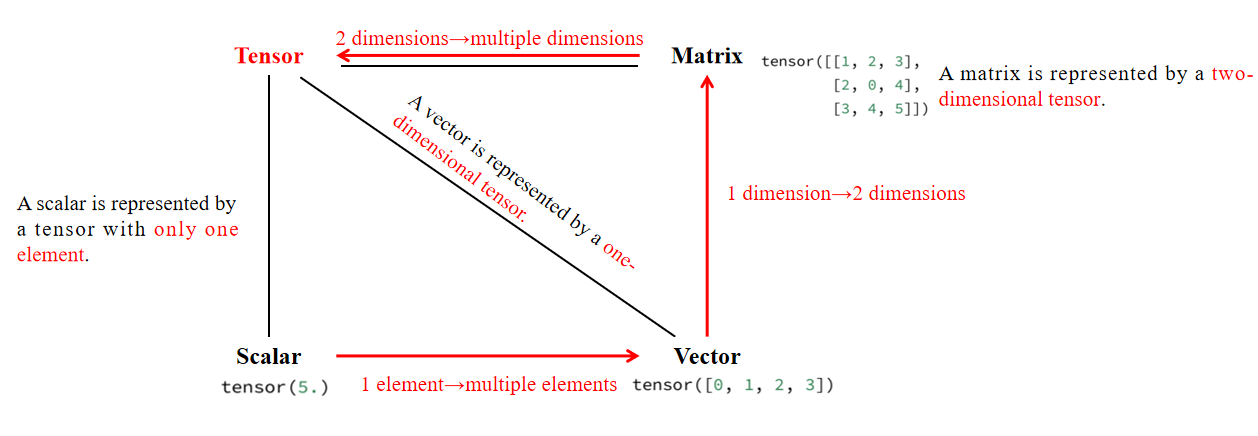
2. 范数

image-20250529115216426

• 表示向量长度或两个点之间的欧氏距离（直线距离）。
• PyTorch 示例：torch.norm(tensor([3, -4.0])) = 5

image-20250529115327789

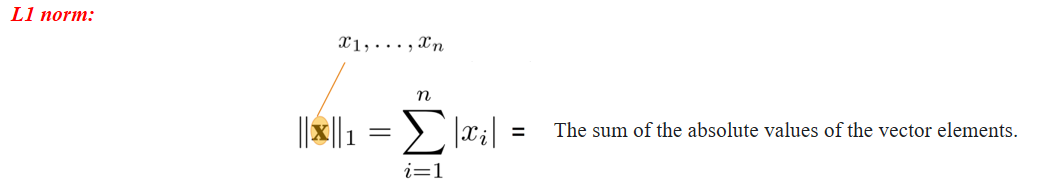
• 表示所有元素绝对值的总和。
• 常用于模型稀疏化（如 Lasso 正则化）。

3. Broadcasting Mechanism

image-20250529114253717

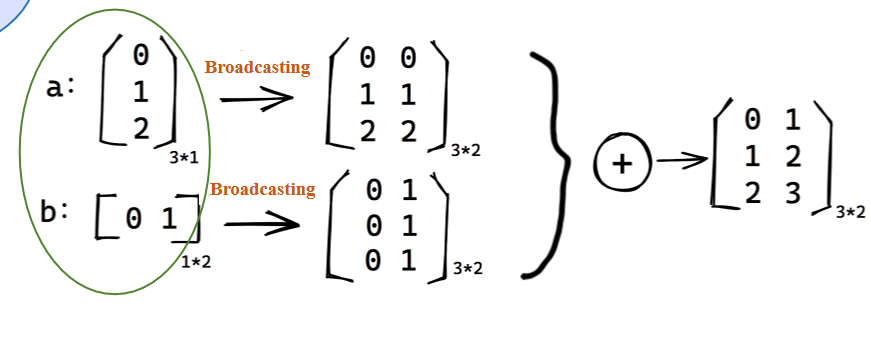
两矩阵无法相加，通过复制列复制行。

1.6 Cross-Entropy loss function

image-20250529115652545

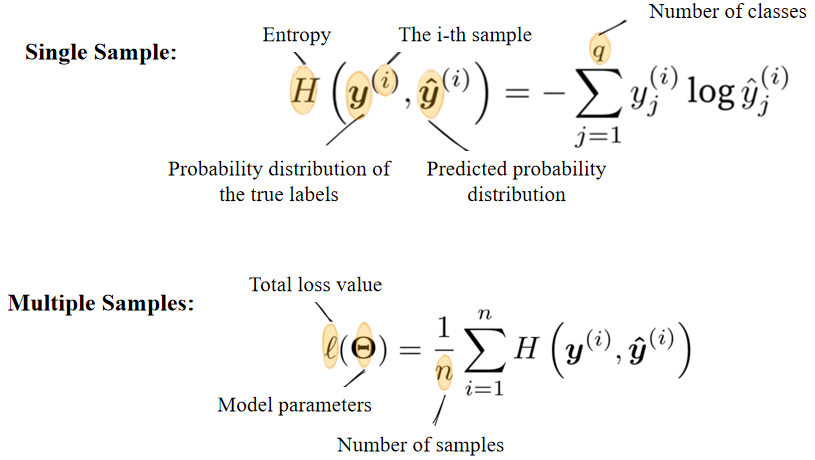
单样本公式（Single Sample）：

$$H({\mathit{y}}^{(i)},{\hat{\mathit{y}}}^{(i)})=-\sum _{j=1}^q{y}_j^{(i)}\log {\hat{y}}_j^{(i)}$$

• $y^{(i)}$：真实标签的概率分布（one-hot 向量）
• ${\hat{y}}^{(i)}$：预测输出的概率分布（Softmax 结果）
• $q$：类别数

多样本总损失（Multiple Samples）：

$$\ell (\mathrm{\Theta })=\frac{1}{n}\sum _{i=1}^{n}H({\mathit{y}}^{(i)},{\hat{\mathit{y}}}^{(i)})$$

• $\mathrm{\Theta }$：模型参数
• $n$：样本数量
• 总体思想：平均每个样本的交叉熵损失

信息论核心思想：

• 稀有事件 → 概率低 → 不确定性高 → 意外程度大 → 含信息量大

• 概率分布的**熵（Entropy）**度量的是“不确定性”

  $$H(p)=-\int p(x)\log p(x)$$

• **交叉熵（Cross-Entropy）**度量的是：用分布 $q(x)$ 来编码 $p(x)$ 时的代价

  $$H(p,q)=-\int p(x)\log q(x)$$

在深度学习中，我们用真实标签的分布作为 $p(x)$，预测分布作为 $q(x)$，用交叉熵衡量两者差距。

1.7 评估模型效果

image-20250529115917769

2. Key components 01

image-20250529121914212

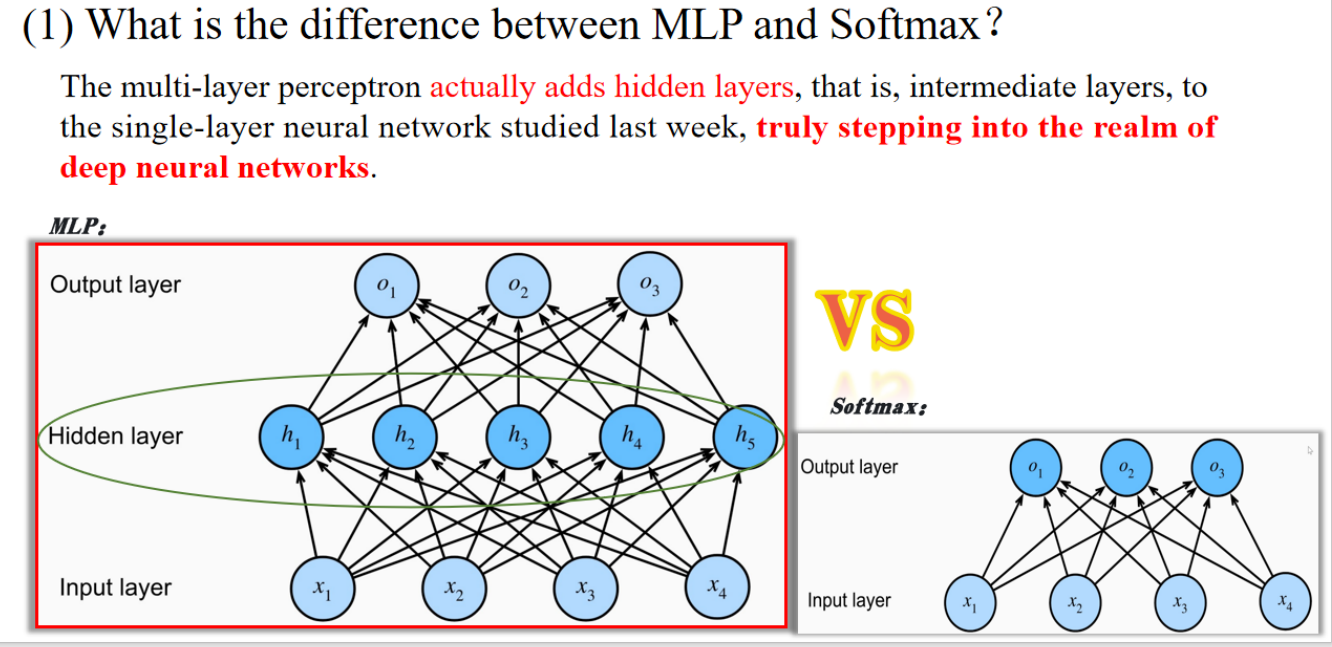
核心解释：

• MLP 与 Softmax 回归的主要区别是：MLP 增加了隐藏层（hidden layers）
• 添加隐藏层之后，就形成了真正意义上的深度神经网络（deep neural networks）
• Softmax 是一种单层神经网络，只能表示线性映射
• MLP 则可以表示更复杂的非线性关系

image-20250529122122097

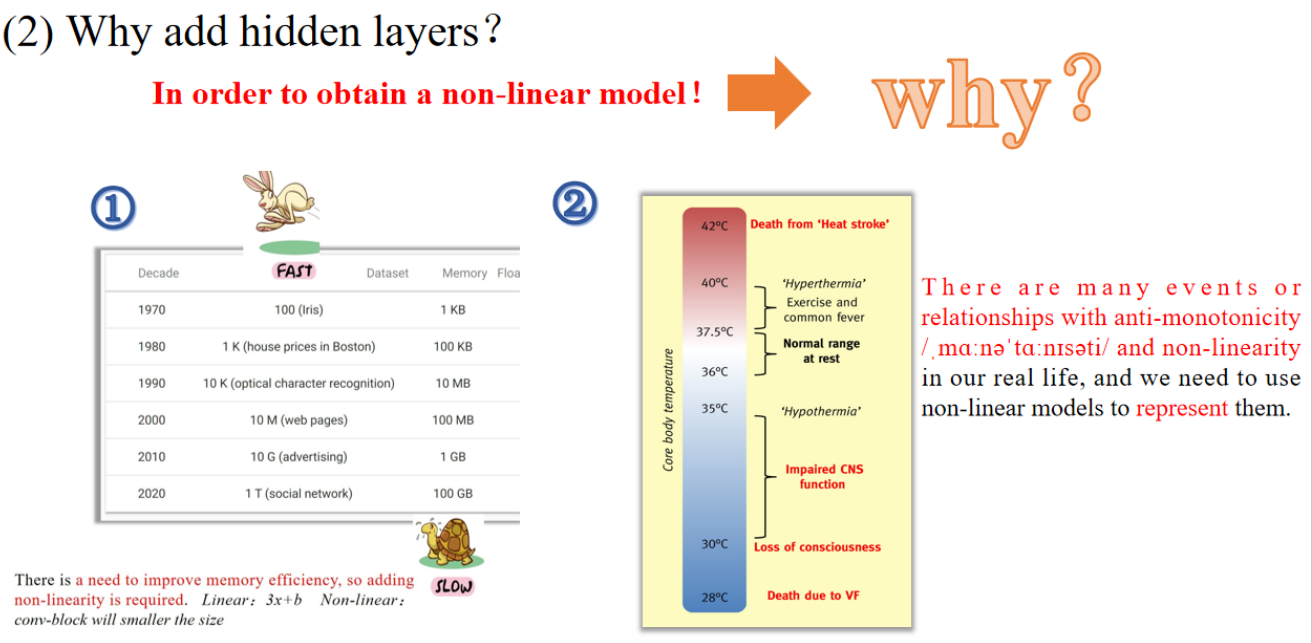
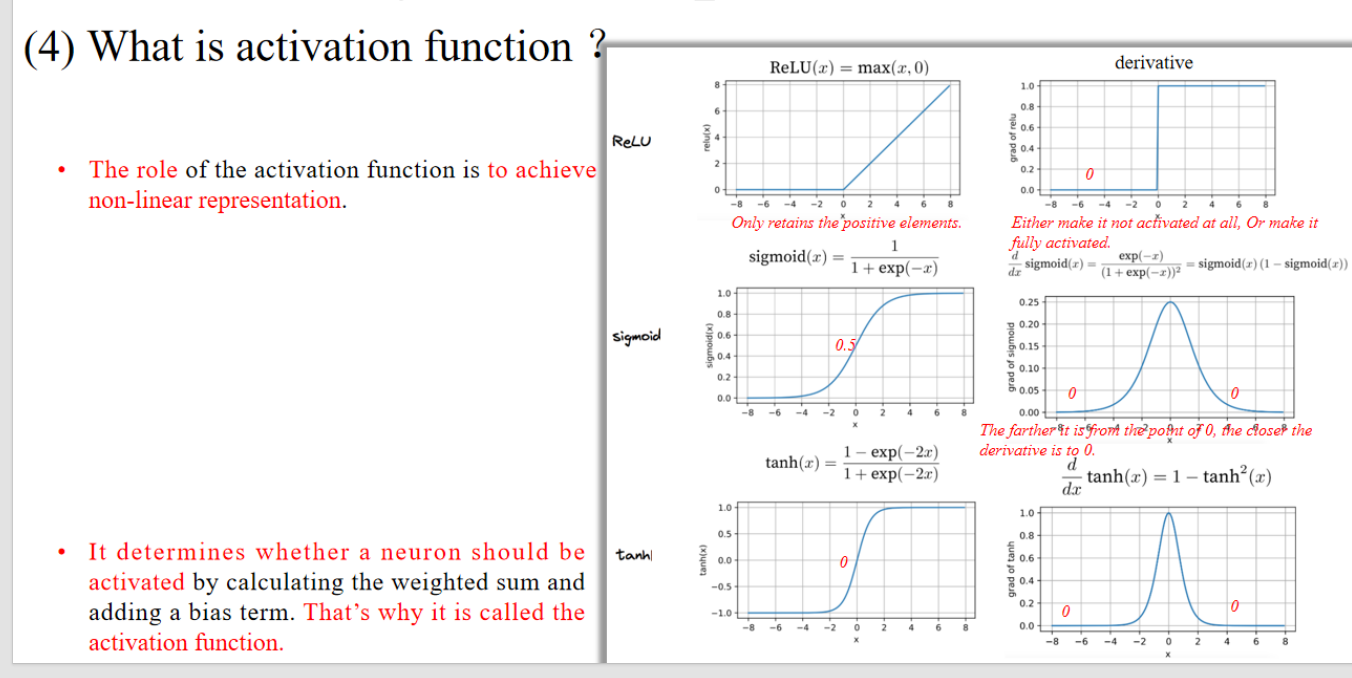
核心解释：

• 为了获得一个非线性模型（non-linear model）
• 现实生活中有很多关系是非线性、非单调的（如体温与健康之间的关系）
  • 举例：过热或过冷都会有危险，表现为“非单调关系”

单词：

• monotonicity 单调性

image-20250529122857677

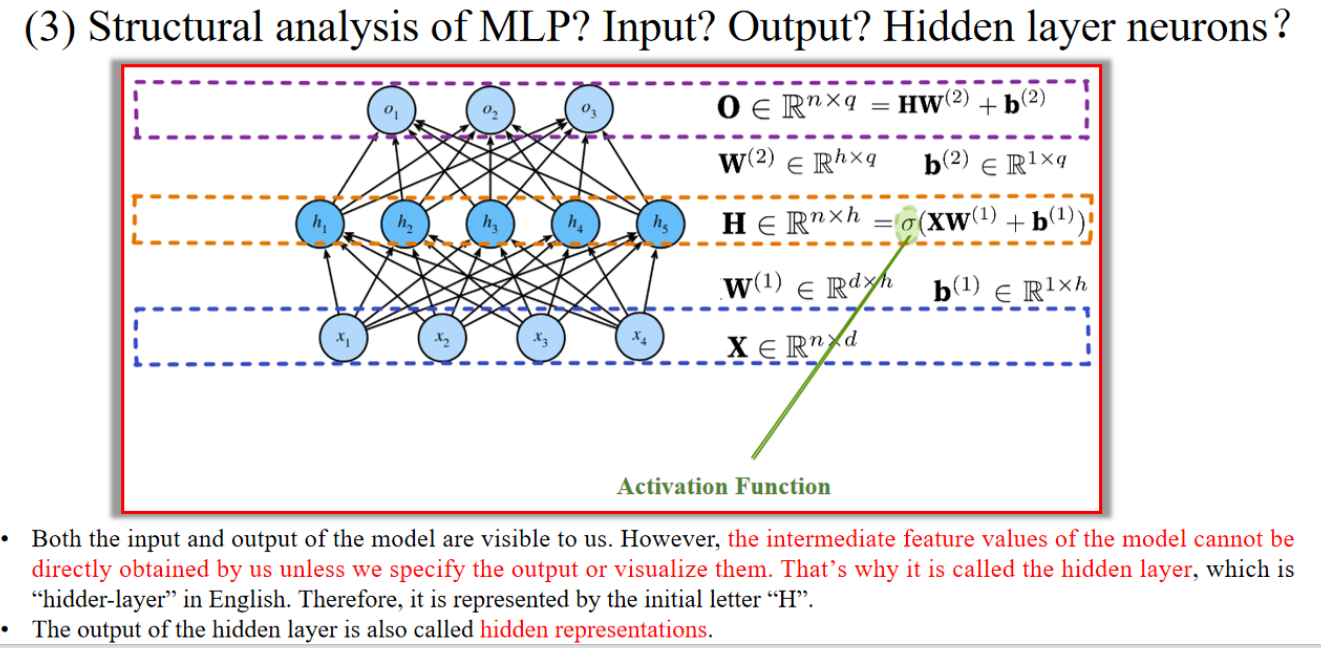
假设我们做一个图片分类任务：

• 每张图像有 4 个像素点 → 输入特征数 $d=4$
• 一次输入 3 张图片 → 样本数 $n=3$
• 我们设计隐藏层神经元为 5 个 → $h=5$
• 要分成 3 类（猫/狗/蛇） → 输出类别数 $q=3$

那么矩阵维度为：

符号	含义	尺寸
$\mathbf{X}$	输入	$3\times 4$
${\mathbf{W}}^{(1)}$	输入层 → 隐藏层 权重	$4\times 5$
${\mathbf{b}}^{(1)}$	偏置	$1\times 5$
$\mathbf{H}$	隐藏层输出	$3\times 5$
${\mathbf{W}}^{(2)}$	隐藏层 → 输出层 权重	$5\times 3$
${\mathbf{b}}^{(2)}$	偏置	$1\times 3$
$\mathbf{O}$	输出得分（logits）	$3\times 3$

image-20250529123419427

image-20250529165120007

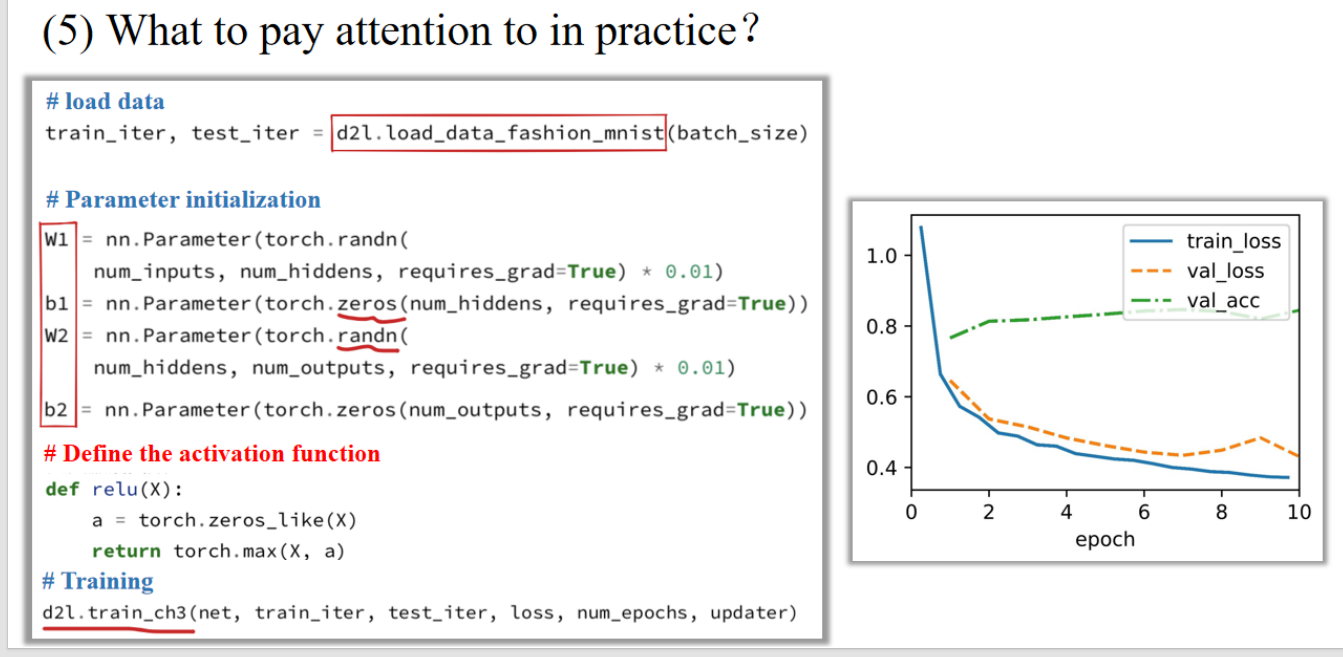
3. Key components 02

3.1 什么是模型泛化？

image-20250529171430066

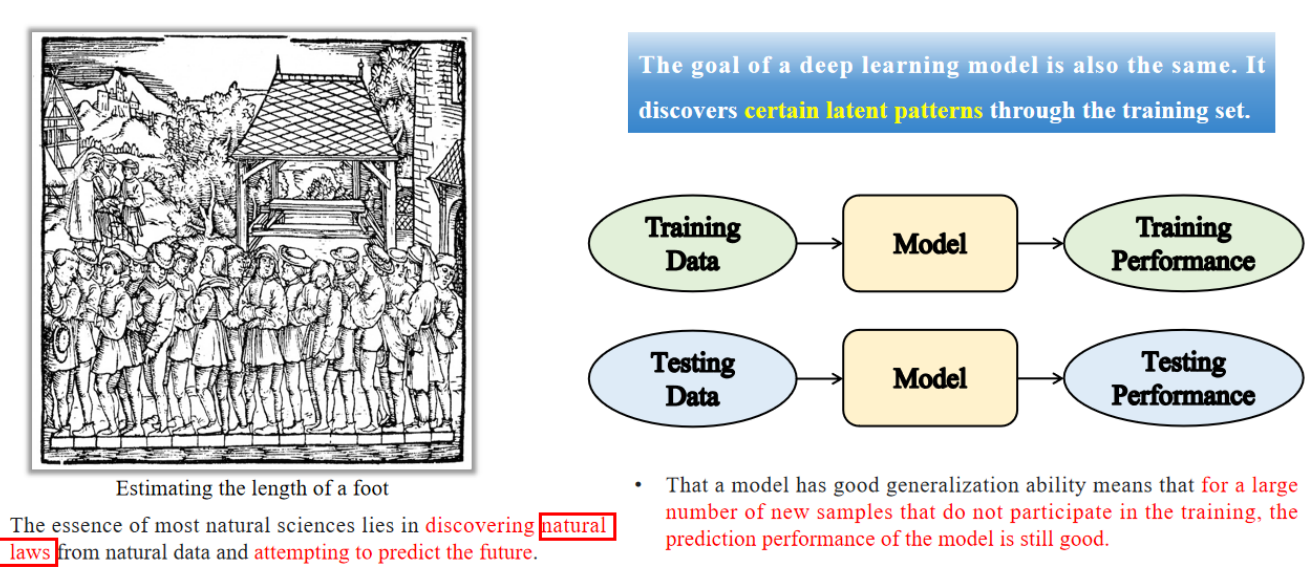
Model generalization: The goal of a deep learning model is also the same. It discovers certain latent patterns through the training set.

3.2 如何判断泛化能力

image-20250529171604368

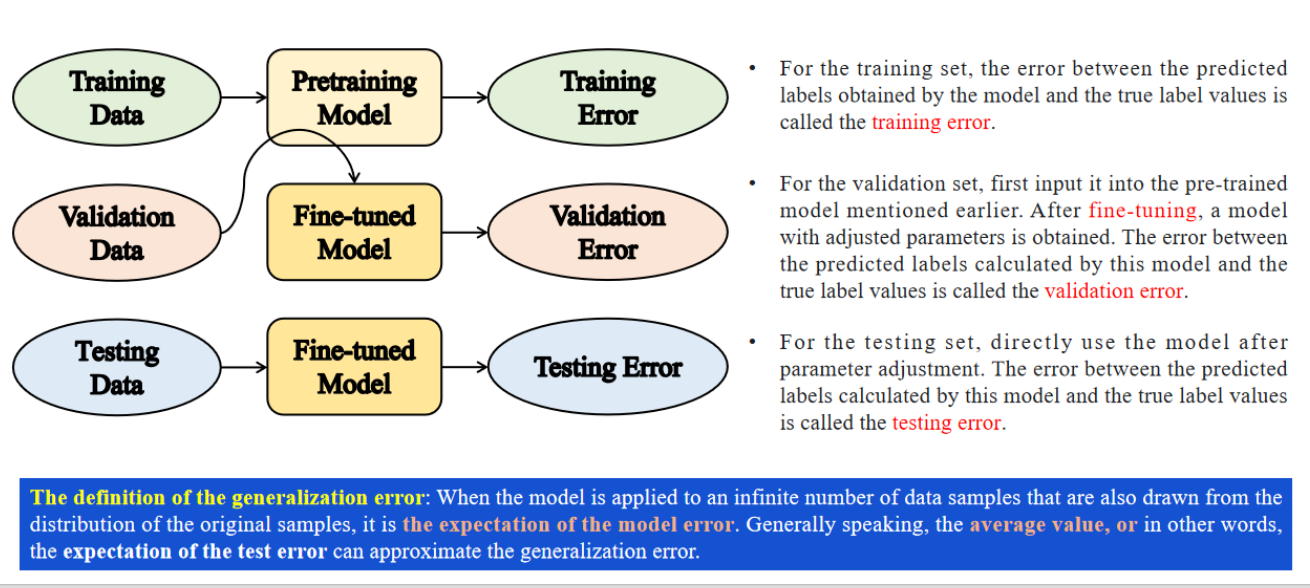
• 单词：
  • fine-tuning 微调。
• 验证集用来微调参数。

3.3 如何提高泛化能力——早停

image-20250529172849366

通俗讲解：
现实中我们不能拿测试集调试模型（因为没标签）。所以用一部分训练数据做“验证集”，边训练边监控。如果发现模型在验证集上的表现不再变好，就提前“刹车”停止训练，避免“死记硬背”。

image-20250529173203288

上图讲了怎么划分数据集。K折交叉验证，把每一份都当做一次验证集其他的当训练集，这样所有数据都当过验证集。

image-20250529173928237

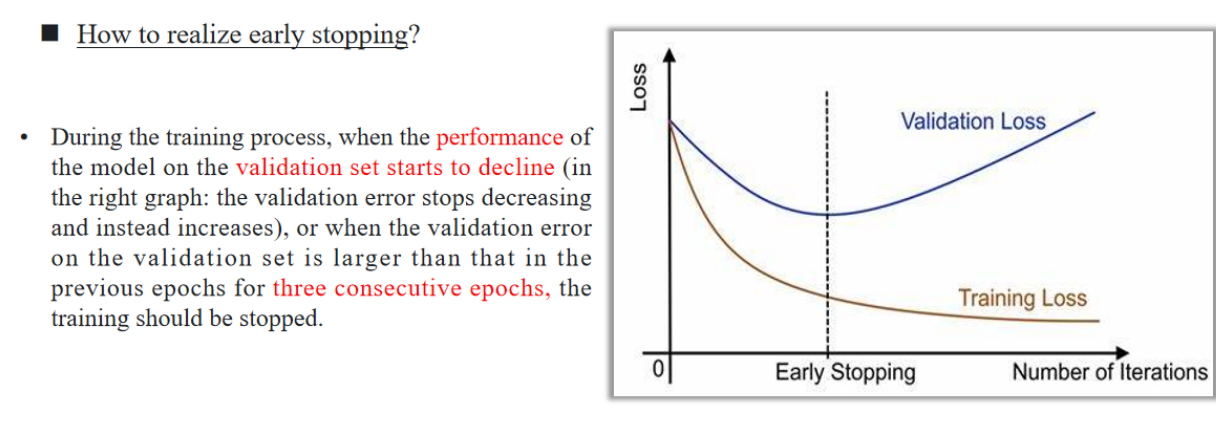
上图为，早停的依据

在训练过程中，当模型在验证集上的性能开始下降时（如右图所示：验证误差不再减少，反而开始增加），或者当验证集上的误差连续三个训练周期（epoch）都比之前的高，那么就应该停止训练。

• 单词：
  • consecutive epochs 连续周期

image-20250529174540305

3.4 weight decay

image-20250529175328088

模型复杂度太高容易过拟合，太低不能很好地学习数据。

• 单词：
  • weight decay ：权重衰减

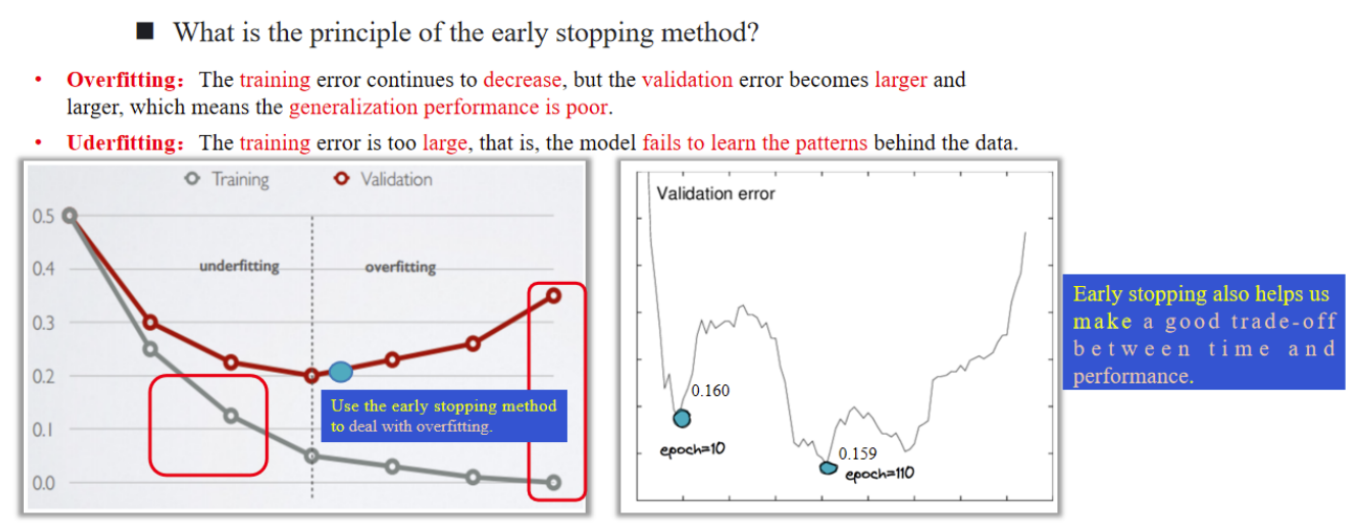
图中曲线说明：

• 横轴是模型复杂度，纵轴是损失（loss）；
• 模型太简单（左侧）时会欠拟合，训练损失和泛化损失都高；
• 模型太复杂（右侧）时训练损失低，但泛化损失（generalization loss）上升；
• weight decay 的目标是把模型从“过拟合区域”往“最优区”拉。

image-20250529180012622

解释：

• 第二项是正则项，惩罚太大的权重；
• $\lambda$：正则化系数，越大说明“惩罚越严”；
• $\parallel \mathbf{w}{\parallel }^2$：权重的平方和，相当于使用 L2 范数的平方；
• 目的：限制模型参数的规模，防止过度拟合。

Note解释：

• A：$\lambda$ 越小，对权重限制越少，越大限制越强；
• B：我们使用平方项，是为了计算更方便（不用开根号）。

单词：

• penalty term 惩罚项
• square root 平方根

image-20250529180557513

• The brain clears out the useless connections between neurons.
  大脑会清除没用的神经连接；

• These connections correspond to the weights in our deep learning.
  神经连接可以类比为神经网络中的“权重”；

• By using weight decay to restrict the useless weights, we can avoid overfitting and thus achieve a better model generalization effect.
  使用 weight decay 限制这些“没用的连接”，能避免过拟合，提升泛化能力。

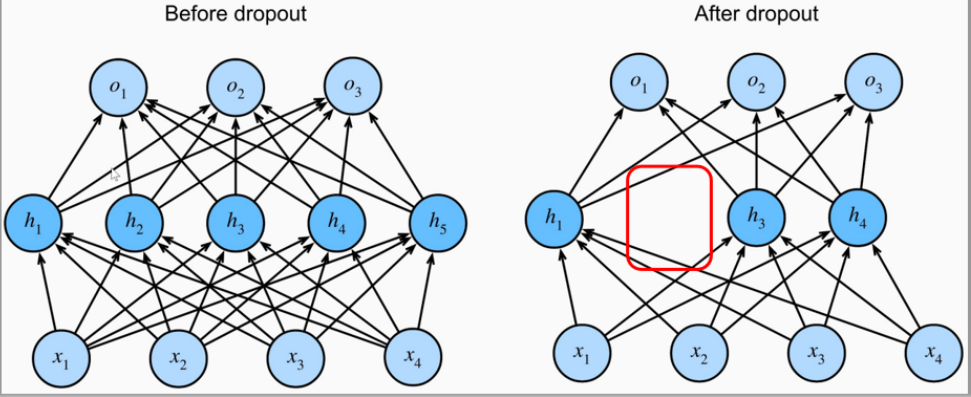
3.5 dropout

image-20250529181023489

• As a result, it avoids an overly sensitive response to minor changes or noises in the input data and exhibits a certain degree of smoothness.
  因此，它能够避免模型对输入数据中的微小变化或噪声过度敏感，呈现出一定的平滑特性。

• During the training process, dropping out some neurons (setting the nodes to zero) is equivalent to injecting noise.

• 单词：

  • inject 加入，注射

image-20250529181428015

image-20250529181814364

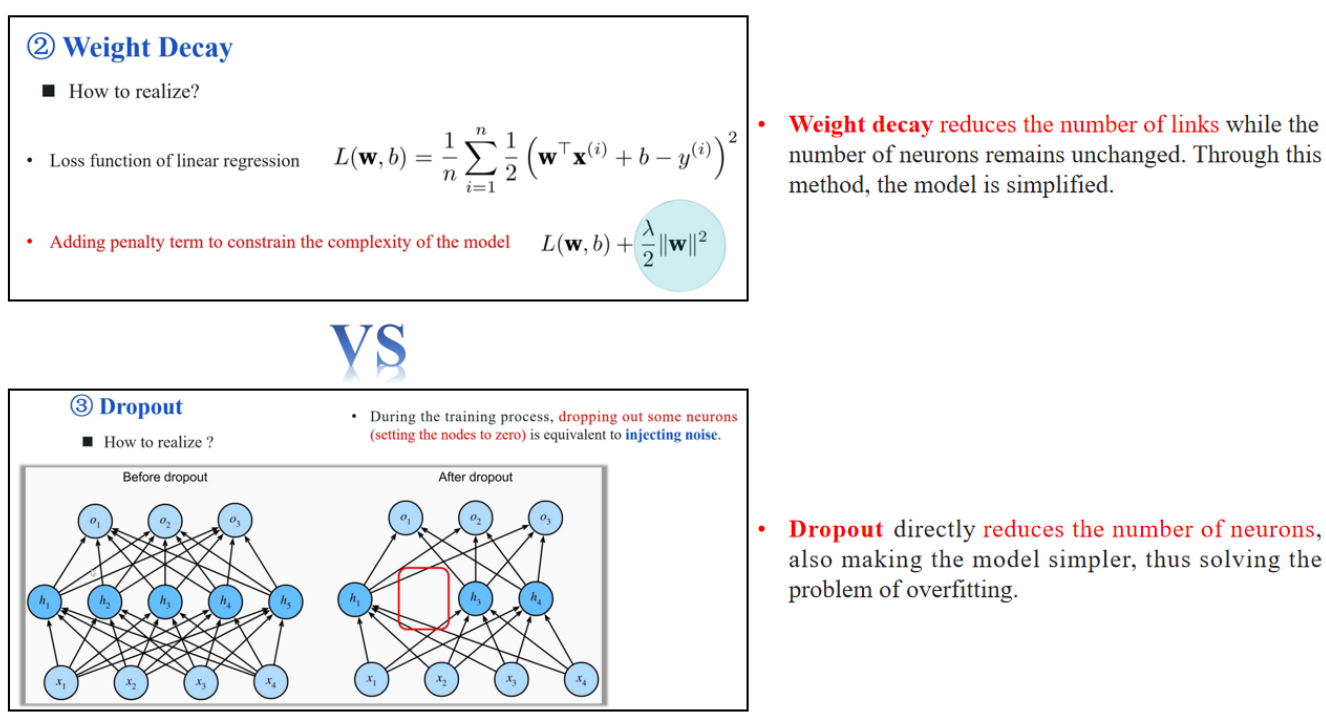
对象	权重衰减（Weight Decay）	Dropout
操作单位	箭头上的权重（连接强度）	整个神经元节点及其连接
是否删除神经元	❌ 不删，只让连接“变弱”	✅ 直接删掉神经元（训练时临时删）
数量减少体现	箭头数不变，但权重接近 0，相当于无效连接	箭头和节点都消失，结构真的变简单
应对问题	控制模型复杂度，抑制过拟合	增加鲁棒性、防止某些神经元过度依赖

数学过程

image-20250529182947223

$$\mathbb{E}[h^{\prime }]=h$$

表示的是 —— Dropout 之后的期望输出值，应该等于原始值。

✅ 举个例子：

假设神经元输出 $h=10$，Dropout 概率 $p=0.2$，意思是 20% 的概率将该神经元“丢弃”。

那么，根据 Dropout 的规则：

• 有 20% 的概率我们会把 $h^{\prime }=0$（就是“drop 掉了”）
• 有 80% 的概率我们会把 $h^{\prime }=\frac{10}{1-0.2}=\frac{10}{0.8}=12.5$

✅ 看看期望值怎么算：

$$\mathbb{E}[h^{\prime }]=0\times 0.2+12.5\times 0.8=0+10=10$$

也就是说，虽然我们随机地丢掉了神经元，但我们对剩下的神经元做了缩放（乘上 $\frac{1}{1-p}$），保证整体的“平均输出值”没变！

image-20250529183540494

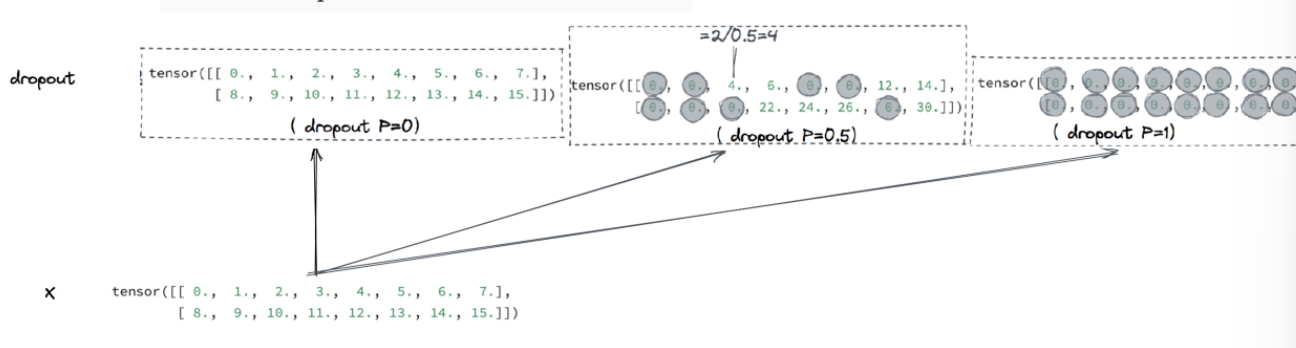
✅ 原始输入张量（X）：

tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])

这是一组模拟神经元的输出，共两行（表示 batch size 为 2），每行 8 个值（表示 8 个神经元输出）。

---

✅ Dropout 应用后效果：

1. dropout P=0：

• 表示 不丢弃任何神经元（p=0）
• 所以输出张量 完全等于原始输入

tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])

---

2. dropout P=0.5：

• 表示 50% 概率将某个神经元置为 0（丢弃）
• 例如图中把偶数位置“drop 掉”了（不是固定的，实际是随机的）
• 剩下的值要乘以 $\frac{1}{1-p}=\frac{1}{0.5}=2$，进行放大，保持期望一致。

输出类似：

tensor([[ 0.,  4.,  0.,  8.,  0., 12.,  0., 14.],
        [ 0., 18.,  0., 22.,  0., 26.,  0., 30.]])

（说明：原来是 2、4、6...，现在变成 4、8、12...，而 1、3、5 被置 0 了）

---

3. dropout P=1：

• 表示 100% 丢弃，所有神经元都被 Drop 掉
• 所有值全部变成 0：

tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]])

---

✅ 总结通俗理解：

dropout 概率 $p$	会发生什么	放大倍数	输出效果
0	什么都不丢	无需放大	原样输出
0.5	随机丢一半	剩下的 ×2	有的为0，有的变大
1	全部丢弃	全变成0	没有信息传递

image-20250529183651978

image-20250529183727244

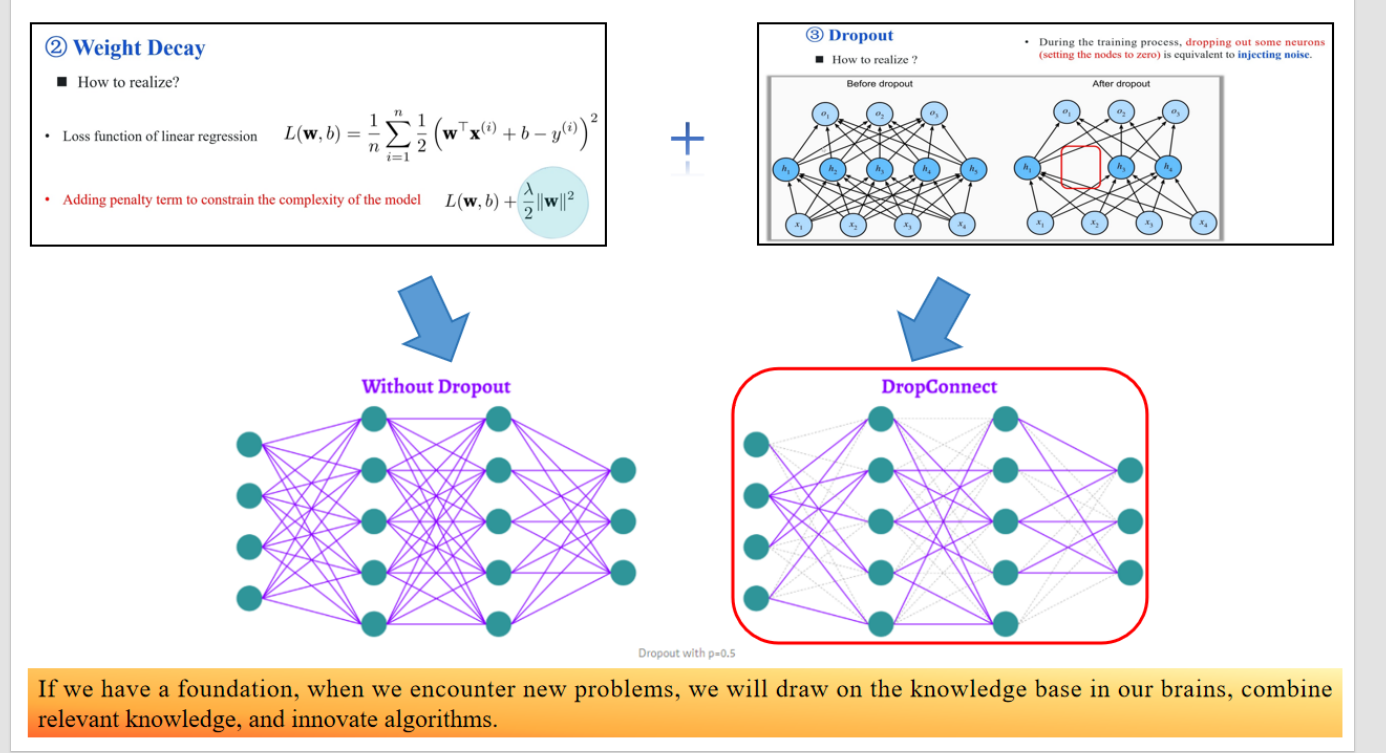
🔹 Without Dropout（左下角)

• 这是一个完整的全连接神经网络。
• 所有神经元之间都有连接。
• 缺点是容易过拟合。

🔹 DropConnect（右下角）

• 是 Dropout 的变种。
• Dropout 是“丢神经元”，即整个神经元输出为 0。
• DropConnect 是“丢连接”，即某些权重直接被置为 0，像断开电线一样。
• 它提供了更细粒度的正则方式，可以更灵活地控制模型复杂度。